Students should refer to Worksheets Class 12 Physics Nuclei Chapter 13 provided below with important questions and answers. These important questions with solutions for Chapter 13 Nuclei have been prepared by expert teachers for Class 10 Science based on the expected pattern of questions in the class 10 exams. We have provided Worksheets for Class 12 Physics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Nuclei Worksheets Class 13 Physics
Question: 1 MeV positron encounters a 1 MeV electron travelling in opposite direction.
What is the wavelength of photons produced? (Given rest mass energy of electron or positron
= 0.512 MeV and h = 6.62 × 10–34 Js)
(a) 8.2 × 10–11 m
(b) 8.2 × 10–13 m
(c) 8.2 × 10–12 m
(d) 8.2 × 10–9 m
Answer:
B
Question: The ratio of the nuclear radii of the gold isotope 19779Au and silver isotope 10747Ag is
(a) 1.23
(b) 0.216
(c) 2.13
(d) 3.46
Answer:
A
Question: Let mp be the mass of a proton, mn the mass of a neutron, M1 the mass of a 2010 Ne nucleus and M2 the mass of a 4020Ca nucleus. Then
(a) M2 = M1
(b) M2 > 2M1
(c) M2 = 2M1
(d) M1 < 10 (mn + mp)
Answer:
D
Question: Light energy emitted by star is due to
(a) breaking of nuclei
(b) joining of nuclei
(c) burning of nuclei
(d) reflection of solar light
Answer:
B
Question: The mass of proton is 1.0073 u and that of neutron is 1.0087 u (u = atomic mass unit). The binding energy of 42 He, if mass of 42He is 4.0015 u
(a) 0.0305 erg
(b) 0.0305 J
(c) 28.4 MeV
(d) 0.061 u
Answer:
C
Question:Two stable isotopes 63Li and 73Li have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u respectively. The atomic weight of lithium is
(a) 6.941 u
(b) 3.321 u
(c) 2.561 u
(d) 0.621 u
Answer:
A
Question: The set which represents the isotope, isobar and isotone respectively is

Answer:
D
Question: If in a nuclear fusion reaction, mass defect is 0.3%, then energy released in fusion of 1 kg mass is
(a) 27 × 1010 J
(b) 27 × 1011 J
(c) 27 × 1010 J
(d) 27 × 1013 J
Answer:
D
Question: If the nucleus 13Al27 has a nuclear radius of about 3.6 fm, then 52Te125 would have its radius approximately as
(a) 9.6 fm
(b) 12 fm
(c) 4.8 fm
(d) 6 fm
Answer:
D
Question: The radius of a spherical nucleus as measured by electron scattering is 3.6 fm. What is the mass number of the nucleus most likely to be?
(a) 27
(b) 40
(c) 56
(d) 120
Answer:
A
Question: Boron has two stable isotopes, 105B and 115B.
Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of 115B.
(a) 90.1%
(b) 80.1%
(c) 85.5%
(d) 95% B
Answer:
B
Case Based MCQs
Discovery of Nucleus The nucleus was first discovered in 1911 by Lord Rutherford and his associates by experiments on scattering of a-particles by atoms. He found that the scattering results could be explained, if atoms consist of a small, central, massive and positive core surrounded by orbiting electrons.
The experimental results indicated that the size of the nucleus is of the order of 10–14 m and is thus 10000 times smaller than the size of atom.
Question: Masses of nuclei of hydrogen, deuterium and tritium are in ratio
(a) 1 : 2 : 3
(b) 1 : 1 : 1
(c) 1 : 1 : 2
(d) 1 : 2 : 4
Answer:
A
Question: Ratio of mass of nucleus with mass of atom isv approximately
(a) 1
(b) 10
(c) 103
(d) 1010
Answer:
A
Question: If R is the radius and A is the mass number, then log R versus log A graph will be
(a) a straight line
(b) a parabola
(c) an ellipse
(d) none of these.
Answer:
A
Question: The ratio of the nuclear radii of the mercury isotope 19880Hg and silver isotope 107 47Ag is
(a) 1.23
(b) 0.216
(c) 2.13
(d) 3.46
Answer:
A
Question: Nuclides with same neutron number but different atomic number are
(a) isobars
(b) isotopes
(c) isotones
(d) none of these
Answer:
C
Nuclear Energy A heavy nucleus breaks into comparatively lighter nuclei which are more stable compared to the original heavy nucleus. When a heavy nucleus like uranium is bombarded by slow moving neutrons, it splits into two parts releasing large amount of energy. The typical fission reaction of 92U235.
92U235 + 0n1 → 56Ba141 + 36Kr92 + 30n1 + 200 MeV
The fission of 92U235 approximately released 200 MeV of energy.
Question: The release in energy in nuclear fission is consistent with the fact that uranium has
(a) more mass per nucleon than either of the two fragments
(b) more mass per nucleon as the two fragment
(c) exactly the same mass per nucleon as the two fragments
(d) less mass per nucleon than either of two fragments.
Answer:
A
Question: If 200 MeV energy is released in the fission of a single nucleus of 235 92U, the fissions which are required to produce a power of 10 kW is
(a) 3.125 × 1013
(b) 1.52 × 106
(c) 3.125 × 1012
(d) 3.125 × 1014
Answer:
D
Question: A nuclear fission is said to be critical when multiplication factor or K
(a) K = 1
(b) K > 1
(c) K < 1
(d) K = 0
Answer:
A
Question: When 92U235 undergoes fission, about 0.1% of the original mass is converted into energy. The energy released when 1 kg of 92U235 undergoes fission is
(a) 9 × 1011 J
(b) 9 × 1013 J
(c) 9 × 1015 J
(d) 9 × 1018 J
Answer:
B
Question: Einstein’s mass-energy conversion relation
E = mc2 is illustrated by
(a) nuclear fission
(b) atomic transition
(c) rocket propulsion
(d) steam engine
Answer:
A
Assertion & Reasoning Based MCQs
Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is also false
Question: Assertion (A) : For the fission of heavy nuclei, neutrons are more effective than protons.
Reason (R) : Neutrons are heavier than protons.
Answer:
B
Question: Assertion (A) : Energy is released in a nuclear reaction.
Reason (R) : In any nuclear reaction the reactants and resultant products obey the law of conservation of charge and mass only.
Answer:
C
Question: Assertion (A) : Two protons can attract each other.
Reason (R) : The distance between the protons within the nucleus is about 10–15 m.
Answer:
A
Question: Assertion (A) : The nuclear force becomes weak if the nucleus contains too many protons compared to neutrons.
Reason (R) : The electrostatic forces weaken the nuclear force.
Answer:
C
Question: Assertion (A) : There is a chain reaction when uranium is bombarded with slow neutrons.
Reason (R) : When uranium is bombarded with slow neutrons more neutrons are produced.
Answer:
A
Very Short Answer Type Questions
Question: Find the ratio of nuclear radius of 6429Cu and 2713Al
Answer:

Question: What is the radius of the nucleus of 6429Cu?
Answer:
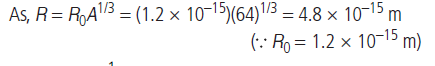
Question: Define the nuclear force?
Answer: Nuclear force is the strongest attractive force which binds the protons and neutrons together inside a tiny nucleus.
Question: Assume that a neutron breaks into a proton and an electron. Find the energy required during this process ?
(Mass of neutron = 1.6725 × 10–27 kg, Mass of proton
= 1.6725 × 10–27 kg, mass of electron = 9 × 10–31 kg)
Answer:

Question: A neutron is absorbed by a 63 Li nucleus with the subsequent emission of an alpha particle. Calculate the energy released, in MeV, in this reaction.
[Given : mass 63 Li = 6.015126 u;
mass (neutron) = 1.0086654 u;
mass (alpha particle) = 4.0026044 u;
Answer: 3Li6 + 0n1 → 2He4 + 1H3 + Q
Total initial mass = 6.015126 + 1.0086654 = 7.0237914 amu
Total final mass = 4.0026044 + 3.01 = 7.0126044 amu
Mass defect, Dm = 7.0237914 – 7.0126044 = 0.0111870 amu
Energy released, Q = 0.0111870 × 931 = 10.415 MeV.
Short Answer Type Questions
Question: 1 92U235 absorbs a slow neutron (thermal neutron) and undergoes a fission represented by
92U235 + 0n1 → 92U236 → 56Ba141 + 36Kr92 + 30n1 + E.
Calculate :
(i) The energy released E per fission.
(ii) The energy released when 1 g of 92U235
undergoes complete fission.
Given : 92U235 = 235.1175 amu (atom),
56Ba141 = 140.9577 amu (atom)
36Kr92 = 91.9264 amu (atom), 0n1 = 1.00868 amu,
1 amu = 931 MeV/c2
Answer: (i) E = [MU + mn – MBa – MKr – 3mn] × 931 = 200.57 MeV
(ii) Energy released =NA /235XE
=200.57X106X1.6X10-19X6.023X1023/235X3.6X106=22.84MWh
Question: Find the disintegration energy Q for the fission event represented by equation
92U235 + 0n1 → 92U236 → 14058Ce + 9440Zr + 20n1
If mass of 92U235 = 235.0439 u, 0n1 = 1.00867 u,
14058Ce = 139.9054 u and 9440Zr = 93.9063 u, find energy released in the process.
Answer: The mass lost in the process,
Dm = 235.0439 + 1.00867 – (139.9054 + 93.9063 + 2.01734) = 0.22353 u
The corresponding energy released
= Δmc2 = 0.22353 × 931 MeV = 208 MeV
Question :Calculate the energy released in fusion reaction :
21H+21H→32He+n,where B.E. of 21H = 2.23 MeV and of 32 He = 7.73 MeV.
Answer: Given fusion reaction,
21H+21H→32He+n,
Energy released = final B.E. – initial B.E.
= 7.73 – (2.23 + 2.23) = 3.27 MeV.
Question: Which is more, the density of lead nuclei or the density of oxygen nuclei?
Answer: We know that the density of solid lead is much greater than the density of gaseous oxygen. But here we are checking about the densities of their nuclei. If the mass of a neutron is m, then mass of nuclei
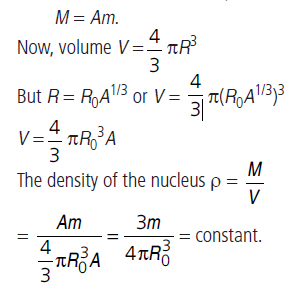
Nuclear density is almost a constant, whether it is lead or oxygen.
Question: If both the number of protons and neutrons in a nuclear reaction is conserved, in what way is mass converted into energy (or vice versa)?
Explain giving one example.
Answer: A certain number of neutrons and protons are brought together to form a nucleus of a certain charge and mass, an energy DEb will be released in this process.
The energy DEb is called the binding energy of the nucleus.
If we separate a nucleus into its nucleons we would have to transfer a total energy equal to DEb, to the nucleons.
Example : 92U235+0n1→14156 Ba+9236 Kr + 310 n + Q
The energy (Q) released was estimated to be 200 MeV per fission and is equivalent to the difference in masses of the nuclei before and after the fission.
