Students should refer to Worksheets Class 10 Mathematics Linear Equations Chapter 3 provided below with important questions and answers. These important questions with solutions for Chapter 3 Linear Equations have been prepared by expert teachers for Class 10 Mathematics based on the expected pattern of questions in the Class 10 exams. We have provided Worksheets for Class 10 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Linear Equations Worksheets Class 10 Mathematics
VERY SHORT ANSWER TYPE QUESTIONS
Question. A motor cyclist is moving along the line x – y = 2 and another motor cyclist is moving along the line x – y = 4 find out their moving direction.
Ans. move parallel
Question. If 2x + 5y = 4, write another linear equation, so that lines represented by the pair are coincident.
Ans. 4x + 10y = 8
Question. A pair of linear equations which has a unique solution x = 2 and y = – 3 is
(a) x + y = 1 and 2x – 3y = – 5
(b) 2x + 5y = – 11 and 2x – 3y = – 22
(c) 2x + 5y = – 11 and 4x + 10y = – 22
(d) x – 4y – 14 = 0 and 5x – y – 13 = 0
Ans. (c) 2x + 5y = – 11 and 4x + 10y = – 22
Question. If the lines given by 3x + 2ky = 2 and 2x + 5y = 1 are parallel, then the value of k is _______ .
Ans. k = 15/4
Question. The area of the triangle formed by the lines x = 3, y = 4 and x = y is _____ .
Ans. 1/2 sq. unit
Question. What is the value of p, for which the pair of linear equations x + y = 3 and 3x + py = 9 is inconsistent.
Ans. p = 3
Question. If a pair of linear equations in two variables is consistent, then the lines represented by two equations are:
(a) Intersecting
(b) Parallel
(c) always coincident
(d) intersecting or coincident
Ans. (d) intersecting or coincident
Question. Write the solution of y = x and y = –x.
Ans. (0, 0)
Question. One of the common solution of ax + by = c and y axis is
(a) (0, c/b)
(b) (0, b/c)
(c) (c/b, 0)
(d) 0, – c/b)
Ans. (a) (0, c/b)
Question. For what value of p, system of equations 2x + py = 8 and x + y = 6 have no solution.
Ans. p = 2
SHORT ANSWER TYPE (I) QUESTIONS
Question. ABCDE is a pentagon with BE || CD and BC || DE, BC is perpendicular to CD If the perimeter of ABCDE is 21 cm, find x and y.

Ans. x = 5, y = 0
Question. The difference of two numbers is 66. If one number is four times the other, find the numbers.
Ans. 88, 22
Question. Solve for x and y
3x + 2y = 11 and 2x + 3y = 4
Also find p if p = 8x + 5y
Ans. x = 5, y = – 2, p = 30
Question. Form a pair of linear equations for: The sum of the numerator and denominator of the fraction is 3 less than twice the denominator. If the numerator and denominator both are decreased by 1, the numerator becomes half the denominator.
Ans. x – y = – 3, 2x – y = 1
Question. Solve the pair of linear equations by substitution method x – 7y + 42 = 0 and x – 3y – 6 = 0
Ans. 42, 12
SHORT ANSWERS TYPE (II) QUESTIONS
Question. For what values of a and b the following pair of linear equations have infinite number of solutions?
2x + 3y = 7
a(x + y) – b(x – y) = 3a + b – 2
Ans. a = 5, b = 1
Question. Solve for x and y
5/(x+y) + 1/(x-y) = 2
15/(x+y) – 5/(x-y) = -2
Ans. (3, 2)
Question. Find the value of k for no. solutions
(3k + 1)x + 3y – 2 = 0
(k2 + 1)x + (k – 2)y – 5 = 0
Ans. k = –1
Question. Pinky scored 40 marks in a test getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks were deducted for each wrong answer, then pinky again would have scored 40 marks. How many questions were there in the test?
Ans. 40 questions
Question. Sunita has some `₹ 50 and `₹ 100 notes amounting to a total of `₹ 15,500. If the total number of notes is 200, then find how many notes of `₹ 50 and `₹ 100 each, she has.
Ans. ₹ 50 notes = 90, ₹ 100 notes = 110
LONG ANSWER TYPE QUESTIONS
Question. Solve the pair of equations by reducing them to a pair of linear equations 2x = 8y-1 and 9y = 3x–6
Ans. x = 24, y = 9
Question. A man travels 600 km to his home partly, by train and partly by bus. He takes 8 hours, if he travels 120 km by train and rest by bus. Further, it takes 20 minute longer, if he travels 200 km by train and rest by bus. Find the speeds of the train and the bus.
Ans. 60 km/hr, 80 km/hr
Question. A boat can travel 30 km upstream and 28 km downs stream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream.
Ans. 10 km/hr, 4 km/hr
Question. A boat covers 32 km upstream and 36 km downstream, in 7 hours. Also it Covers 40 km upstream and 48 km downstream in 9 hours. Find the speed of boat in still water and that of the stream.
Ans. 10 km/hr, 2 km/hr
Question. Find the values of a and b for infinite solutions
(i) 2x – (a – 4)y = 2b + 1
4x – (a – 1)y = 5b – 1
(ii) 2x + 3y = 7
2ax + ay = 28 – by
Ans. (i) 7, 3
(ii) 4, 8
Question. Determine graphically, the vertices of the triangle formed by the times y = x, 3y = x and x + y = 8.
Ans. Vertices of the triangle are (0, 0) (4, 4) (6, 2).
Question. ABCD is a rectangle. Find the perimeter of the rectangle.
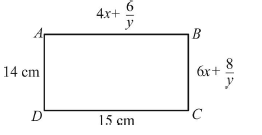
Ans. x = 3 and y = 2
Question. Vijay had some bananas and he divided them into two lots A and B. He sold the first lot at the rate of `₹ 2 for 3 bananas and the second lot at the rate of `₹ 1 per banana and got a total of `₹ 400. If he had sold the first lot at the rate of `₹ 1 per banana and the second lot at the rate of `₹ 4 for 5 bananas, his total collection would have been `₹ 460. Find the total number of bananas he had.
Ans. Let the no. of bananas in lots A be x and in lots B be y
Case I : (2/3)x + y = 400 ⇒ 2x + 3y = 1200
Case 2 : x + (4/5)y = 460 ⇒ 5x + 4y = 2300
x = 300, y = 200, Total bananas = 500.
Question. A nirudh takes 3 hours more than Nishi to walk 30 km. But if Anirudh doubles his speed, he is ahead of Nishi by 1½ hours. Find their speed fo walking.
Ans. 10/3 km/hr, 5 km/hr
