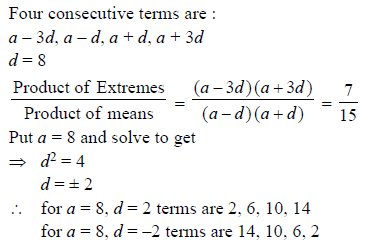Worksheets Chapter 5 Arithmetic Progression Class 10 Mathematics

Students should refer to Worksheets Class 10 Mathematics Arithmetic Progression Chapter 5 provided below with important questions and answers. These important questions with solutions for Chapter 5 Arithmetic Progression have been prepared by expert teachers for Class 10 Mathematics based on the expected pattern of questions in the Class 10 exams. We have provided Worksheets for Class 10 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.

Arithmetic Progression Worksheets Class 10 Mathematics

VERY SHORT ANSWER TYPE QUESTIONS

Question. Find the common difference of A.P. 4(1/9), 4(2/9), 4(1/3), ………….
Ans. d = a₂ – a₁ = 1/9

Question. What is value of a₁₆ for the A.P. – 10, – 12, – 14, – 16, …….
Ans. a₁₆ = a + 15d = – 40

Question. Write the sum of first n even numbers.
Ans. 2 + 4 + 6 + … + 2n = n/2 [2 + 2n] = n(n + 1)

Question. Write the n^th term of odd numbers.
Ans. 1, 3, 5, ……
a_n = 1 + (n – 1)2 = 2n – 1.

Question. For what value of p, the following terms are three consecutive terms of an A.P. 4/5, p, 2.
Ans. p = 7/5

Question. Find the nth term of the A.P. – 10, – 15, – 20, – 25, ………..
Ans. a_n = a + (n – 1)d = – 5(n + 1)

Question. In the following A.Ps, find the missing terms in the boxes :
(a) 2, __ , 26
(b) __ , 13, __ , 3
(c) 5, __ , __ ,9(1/2)
(d) – 4, __ , __ , __ , __ , 6
(e) __ , 38, __ , __ , __ , – 22
Ans.

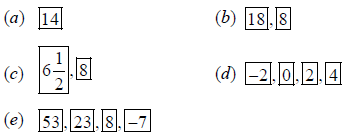
Question. The common difference of the A.P. 2 , 2 2 , 3 2 , 4 2 …… is
(A) √2
(B) 1
(C) 2√2
(D) –√2
Ans. (A) √2

Question. In an A.P. if d = – 4, n = 7, a_n = 4, then a is
(A) 6
(B) 7
(C) 120
(D) 28
Ans. (D) 28

Question. What is the common difference of an A.P. in which a₁₈ – a₁₄ = 32 ?
(A) 8
(B) – 8
(C) – 4
(D) 40
Ans. (A) 8

Question. 30th term of the A.P. 10, 7, 4 …. is
(A) 97
(B) 77
(C) –77
(D) –87
Ans. (C) –77

Question. The list of numbers – 10, – 6, – 2, 2, … is
(A) An A.P. with d = – 16
(B) An A.P. with d = 4
(C) An A.P. with d = – 4
(D) Not an A.P.
Ans. (B) An A.P. with d = 4

Question. The 11^th term from the last term of an A.P. 10, 7, 4, …., – 62 is
(A) 25
(B) –32
(C) 16
(D) 0
Ans. (B) –32

Question. 2, 5, 9, 14, …. is an A.P. True or False.
Ans. False, ∵ a₂ – a₁ = 5 – 2 = 3
∵ a₃ – a₂ = 9 – 5 = 4

Question. 301 is a term of an A.P. 5, 11, 17, 23 …. True or False.
Ans. False, 301 = 5 + (n – 1) 6
Solving we get n = 151/3 which is not a natural number.
∴ 301 is not a term of this A.P.

SHORT ANSWER TYPE QUESTIONS-I

Question. Find whether (– 150) is a term of A.P. 11, 8, 5, 2, ….. ?
Ans. Let a_n = –150
11 + (n – 1) (– 3) = – 150
Solve and get n is not a natural number. ( n = 164/3 )
∴ Answer is No.

Question. The first term, common difference and last term of an A.P. are 12, 6 and 252 respectively, Find the sum of all terms of this A.P.
Ans. a = 12, d = 6, a_n = 252 ⇒ n = 41
Find S₄₁ = 5412, use S_n = n/2 [2a + (n – 1) d]

Question. How many terms of the A.P. 22, 20, 18, ……. should be taken so that their sum is zero.
Ans. S_n = 0 ⇒ n/2 [44 + (n – 1) (– 2)] = 0.
Solve n = 23

Question. Find the sum of first 15 multiples of 8.
Ans. S₁₅ = 15/2 [2a + 14d]
where a = 8, d = 8
∴ Answer is 960

Question. Is 144 a term of the A.P. 3, 7, 11, ……… ? Justify your answer.
Ans. 144 = 3 + (n – 1) 4
(141/4) +1 = n which is not possible

Question. Is the sequence formed in the following situations an A.P.
(i) Number of students left in the school auditorium from the total strength of 1000 students when they leave the auditorium in batches of 25.
(ii) The amount of money in the account every year when Rs. 100 are deposit annually to accumulate at compound interest at 4% per annum.
Ans. (i) Yes → (1000, 975, 950, 925 …..)
(ii) No → (104, 108.16, 112.48 …..)

Question. Find the sum of even positive integers between 1 and 200.
Ans.

Question. Find the middle term of an A.P. – 6, – 2, 2, …. 58.
Ans. a_n = a + (n – 1) d
58 = – 6 + (n – 1) 4
find n = 17
Find Middle term using concept of median
= [(n+1)/2]^th term = 9th term
a₉ = – 6 + 8(4) = 26

Question. Show that (a – b)², (a² + b²) and (a + b²) are in A.P.
Ans.

Question. If 4m + 8, 2m² + 3m + 6, 3m² + 4m + 4 are three consecutive terms of an A.P. find m.
Ans. 

SHORT ANSWER TYPE QUESTIONS-II

Question. The sum of 5^th and 9^th terms of an A.P. is 72 and the sum of 7^th and 12^th term is 97. Find the A.P.
Ans. a₅ + a₉ = 72
a₇ + a₁₂ = 97
Solve these equations to get a and d, a = 6, d = 5
∴ A.P., 6, 11, 16, 21, 26, …….

Question. Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
Ans. Numbers divisible by both 2 and 5
⇒ Numbers divisible by 10.
Numbers between 101 and 999 divisible by 2 and 5 both 110, 120, 130, 140, …, 990.
Use a_n = 990 to get n = 89.

Question. Find the middle terms of the A.P. 7, 13, 19, ……., 241.
Ans. Same as Q.27, n = 40 Middle terms are a₂₀, a₂₁
∴ Answer is 121, 127

Question. If S_n = 4n – n² in an A.P. find the A.P.
Ans. S_n = 4n – n²
S₁ = a₁ = 4 – 1 = 3
S₂ = a₁ + a₂ ⇒ a₂ = 1 , A.P. 3, 1, – 1, …
S₃ = a₁ + a₂ + a₃ ⇒ a₃ – 1

Question. If S_n, the sum of first n terms of an A.P. is given by Sn = 5n² + 3n, then find its n^th term and common difference.
Ans. S_n = 5n² + 3n
Find a_n = S_n – S_n–1 = 10 n – 2
Use it to get d = 10

Question. How many terms of the A.P. 9, 17, 25, ….. must be taken to give a sum of 636?
Ans. n = 12, n = 53/4

Question. Which term of the A.P. 3, 15, 27, 39 …. will be 120 more than its 21^st term?
Ans. Let a_n = 120 + a₂₁
3 + (n – 1)d = 120 + [3 + 20d]
3 + (n – 1)12 = 120 + [3 + 20 × 12]
= 120 + 243
(n – 1)12 = 363 – 3 = 360
n = 31

Question. Find the sum of odd numbers between 0 and 50.
Ans. Odd numbers between 0 to 50
1, 3, 5, 7, …, 49
a_n = 49
a + (n – 1)d = 49
1 + (n – 1)2 = 49
n = 25
S_n = n/2 [a + l]
S₂₅ = 25/2 [1 + 49] = 25 × 25 = 625

LONG ANSWER TYPE QUESTIONS

Question. The sum of first n terms of an A.P. is 5n² + 3n. If the m^th term is 168, find the value of m. Also find the 20^th term of the A.P.
Ans. S_n = 5n² + 3n
S₁ = a₁ = 8
S₂ = a₁ + a₂
26 = 8 + a₂ ⇒ a₂ = 18
d = 18 – 8 = 10
a_m = 168 ⇒ a + (m – 1)d = 168
8 + (m – 1)10 = 168 ⇒ m = 17

Question. The sum of first 9 terms of an A.P. is 162. The ratio of its 6^th term to its 13^th term is 1:2. Find the first and fifteenth terms of the A.P.
Ans.

Question. If the 4^th term of an A.P. is zero, prove that the 25^th term of the A.P. is three times its 11^th term.
Ans. a₄ = 0 ⇒ a + 3d = 0 ⇒ a = – 3d
a₂₅ = a + 24d = – 3d + 24d = 21d
a₁₁ = a + 10d = – 3d + 10d = 7d
∴ a₂₅ = 3a₁₁

Question. The sum of the first 9 terms of an A.P. is 171 and the sum of its first 24 terms is 996. Find the first term and common difference of the A.P.
Ans. S₉ = 171, S₂₄ = 996
a + 4d = 19, 2a + 23d = 83
Solve to get,
d = 3, a = 7

Question. Find the sum of first 16 terms of an Arithmetic Progression whose 4^th and 9^th terms are –15 and –30 respectively.
Ans. 

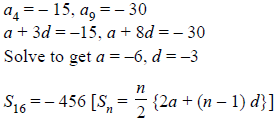
Question. In an A.P. if S₅ + S₇ = 167 and S₁₀ = 235. Find the A.P., where S_n denotes the sum of its first n terms.
Ans. Use S_n = n/2 [2a + (n – 1) d]
S₅ + S₇ = 167 S₁₀ = 235
Solve to get a = 1, d = 5
A.P. = 1, 6, 11, 16, 21, ………

Question. The sum of first 7 terms of an A.P. is 63 and the sum of its next 7 term is 161. Find the 28^th term of this A.P.
Ans. ATQ S₇ = 63,                                 …(1)
Sum of next 7 terms = S₁₄ – S₇ = 161    …(2)
Use S_n = n/2 [2a + (n – 1) d]
Solve (1) and (2) to get a and d then find a₂₈ using a_n = a + (n – 1) d.
a = 3, d = 2
∴ Answer is a₂₈ = 57

Question. The sum of four consecutive numbers in A.P. is 32 and the ratio of the product of the first and last term to the product of two middle terms is 7 : 15. Find the numbers.
Ans.