Students should refer to Worksheets Class 11 Mathematics Permutations and Combinations Chapter 7 provided below with important questions and answers. These important questions with solutions for Chapter 7 Permutations and Combinations have been prepared by expert teachers for Class 11 Mathematics based on the expected pattern of questions in the class 11 exams. We have provided Worksheets for Class 11 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Permutations and Combinations Worksheets Class 11 Mathematics
Question. The number of ways a student can choose a programme out of 5 courses, if 9 courses are available and 2 specific courses are compulsory for every student is
(a) 35
(b) 40
(c) 24
(d) 120
Answer
A
Question. If 56Pr + 6 : 54Pr + 3 = 30800 : 1, then the value of r is
(a) 41
(b) 14
(c) 10
(d) 51
Answer
A
Question. A student has to answer 10 questions, choosing at least 4 from each of parts A and B. If there are 6 questions in Part A and 7 in Part B, in how many ways can the student choose 10 questions?
(a) 266
(b) 260
(c) 256
(d) 270
Answer
A
Question. What is (n + 2)! + (n + 1)!(n − 1)! / (n + 1)!(n − 1)! equal to ?
(a) 1
(b) Always an odd integer
(c) A perfect square
(d) None of these
Answer
C
Question. What is the value of nC0?
(a) 0
(b) ∞
(c) 1
(d) None of these
Answer
C
Question. Given 4 flags of different colours, how many different signals can be generated, if a signal requires the use of 2 flags one below the other?
(a) 12
(b) 13
(c) 14
(d) 15
Answer
A
Question. nCr + 2 nCr–1 + nCr–2 is equal to:
(a) n+2Cr
(b) nCr+1
(c) n–1Cr+1
(d) None of these
Answer
A
Question. Total number of ways of selecting five letters from letters of the word INDEPENDENT is
(a) 70
(b) 72
(c) 75
(d) 80
Answer
B
Question. The number of ways in which 3 prizes can be distributed to 4 children, so that no child gets all the three prizes, are
(a) 64
(b) 62
(c) 60
(d) None of these
Answer
C
Question. There are four bus routes between A and B; and three bus routes between B and C. A man can travel round-trip in number of ways by bus from A to C via B. If he does not want to use a bus route more than once, in how many ways can he make round trip?
(a) 72
(b) 144
(c) 14
(d) 19
Answer
A
Question. Number of different seven digit numbers that can be written using only the three digits 1, 2 and 3 with the condition that the digit 2 occurs twice in each number is
(a) 652
(b) 650
(c) 651
(d) 640
Answer
A
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.
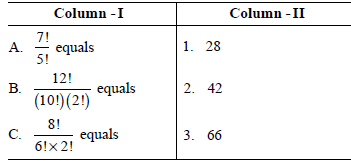
Codes:
A B C
(a) 1 2 3
(b) 1 3 2
(c) 3 2 1
(d) 2 3 1
Answer
D
Question. The number of 4-digit numbers that can be formed with the digits 1, 2, 3, 4 and 5 in which at least 2 digits are identical, is
(a) 505
(b) 45 – 5!
(c) 600
(d) None of these
Answer
A
Question. A car will hold 2 in the front seat and 1 in the rear seat. If among 6 persons 2 can drive, then the number of ways in which the car can be filled is
(a) 10
(b) 20
(c) 30
(d) None of these
Answer
D
Question. (8C1 – 8C2 + 8C3 – 8C4 + 8C5 – 8C6 + 8C7 – 8C8) equals:
(a) 0
(b) 1
(c) 70
(d) 256
Answer
B
Question. To fill 12 vacancies, there are 25 candidates of which five are from scheduled caste. If 3 of the vacancies are reserved for scheduled caste candidates while the rest are open to all, then the number of ways in which the selection can be made
(a) 5C3 × 22C9
(b) 22C9 – 5C3
(c) 22C3 + 5C3
(d) None of these
Answer
A
Question. How many arrangements can be made out of the letters of he word “ MOTHER” taken four at a time so that each arrangement contains the letter ´M´?
(a) 240
(b) 120
(c) 60
(d) 360
Answer
A
Question. ABC is a triangle. 4, 5, 6 points are marked on the sides AB, BC, CA, respectively, the number of triangles on different side is
(a) (4 + 5 + 6)!
(b) (4 – 1) (5 – 1) (6 – 1)
(c) 5! 4! 6!
(d) 4 × 5 × 6
Answer
D
Question. The number of numbers that can be formed with the help of the digits 1, 2, 3, 4, 3, 2, 1 so that odd digits always occupy odd places, is
(a) 24
(b) 18
(c) 12
(d) 30
Answer
B
Question. Every body in a room shakes hands with every body else. If total number of hand-shaken is 66, then the number of persons in the room is
(a) 11
(b) 10
(c) 12
(d) 19
Answer
C
Question. The total number of ways of selecting six coins out of 20 one rupee coins, 10 fifty paise coins and 7 twenty five paise coins is:
(a) 37C6
(b) 56
(c) 28
(d) 29
Answer
C
Question. The number of ways of dividing 52 cards amongst four players so that three players have 17 cards each and the fourth player have just one card, is
(a) 52!/(17!)3
(b) 52!
(c) 52!/17!
(d) None of these
Answer
A
Question. How many words (with or without dictionary meaning) can be made from the letters of the word MONDAY, assuming that no letter is repeated, if

Match the statements in column-I with column-II and choose the correct options from the codes given below.
Codes:
A B C
(a) 1 2 3
(b) 3 1 2
(c) 2 1 3
(d) 3 2 1
Answer
B
Question. Ten persons, amongst whom are A, B and C to speak at a function. The number of ways in which it can be done if A wants to speak before B and B wants to speak before C is
(a) 10!/6
(b) 3! 7!
(c) 10P3 . 7!
(d) None of these
Answer
A
Question. In an examination, there are three multiple choice questions and each question has 4 choices. Number of ways in which a student can fail to get all answers correct is
(a) 11
(b) 12
(c) 27
(d) 63
Answer
D
Question. The number of combinations of 4 different objects A, B, C, D taken 2 at a time is-
(a) 4
(b) 9
(c) 6
(d) 7
Answer
B
Question. If the ratio 2nC3 : nC3 is equal to 11 : 1, n equals
(a) 2
(b) 6
(c) 8
(d) 9
Answer
B
Question. How many numbers lying between 999 and 10000 can be formed with the help of the digits 0, 2, 3, 6, 7, 8, when the digits are not repeated?
(a) 100
(b) 200
(c) 300
(d) 400
Answer
C
Question. What is the value of nCn?
(a) 0
(b) ∞
(c) r
(d) 1
Answer
D
Question. Number of 5 digit numbers that can be made using the digits 1 and 2 and in which at least one digit is different.
(a) 30
(b) 25
(c) 28
(d) 31
Answer
A
Question. The number of circles that can be drawn out of 10 points of which 7 are collinear, is
(a) 120
(b) 113
(c) 85
(d) 86
Answer
C
STATEMENT TYPE QUESTIONS
Question. Consider the following statements:
Statement I : The number of diagonals of n-sided polygon is nC2 – n.
Statement II : A polygon has 44 diagonals. The number of its sides are 10.
Choose the correct option from the choices given below.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Both I and II are false
Answer
A
Question. Consider the following statements.
I. nCr + 2 nCr−1+nCr−2 = n+2Cr
II.nCp = nCq ⇒ p = q or p + q = n
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C
Question. Consider the following statements.
I. Value of 15C8 + 15C9 – 15C6 – 15C7 is zero.
II. The total number of 9 digit numbers which have all different digits is 9!
Choose the correct option.
(a) Only I is true
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
A
Question. A committee of 7 has to be formed from 9 boys and 4 girls.
I. In 504 ways, this can be done, when the committee consists of exactly 3 girls.
II. In 588 ways, this can be done, when the committee consists of at least 3 girls.
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C
Question. In an examination there are three multiple choice questions and each question has 4 choices. Number of ways in which a student can fail to get all answers correct, is:
(a) 11
(b) 12
(c) 27
(d) 63
Answer
D
Question. If nC3 + nC4 > n+1C3 then:
(a) n > 6
(b) n > 7
(c) n < 6
d .None of these
Answer
A
Question. The number of numbers that can be formed with the help of the digits 1, 2, 3, 4, 3, 2, 1 so that odd digits always occupy odd places, is:
(a) 24
(b) 18
(c) 12
(d) 30
Answer
B
Question. If x, y and r are positive integers, then xCr + xCr-1 yC1 + xCr-2 yC2 +……+yCr =?
(a) x!y!/r!
(b) (x+y)/r!
(c) x+yCr
(d) xyCr
Answer
C
Question. The number of divisors of 9600 including 1 and 9600 are:
(a) 60
(b) 58
(c) 48
(d) 46
Answer
C
Question. The number of ways in which 5 male and 2 female members of a committee can be seated around a round table so that the two female are not seated together is:
(a) 480
(b) 600
(c) 720
(d) 840
Answer
A
Question. The least value of natural number n satisfying
C(n, 5) + C(n, 6) > C(n + 1, 5) is:
(a) 11
(b) 10
(c) 12
(d) 13
Answer
A
Question. In how many ways 7 men and 7 women can be seated around a round table such that no two women can sit together:
(a) 2 (7!)
(b) 7!×6!
(c) 2 (6!)
(d) 7!
Answer
B
Question. The number of ways that 8 beads of different colours be string as a necklace is:
(a) 2520
(b) 2880
(c) 5040
(d) 4320
Answer
A
Question. There are n seats round a table marked 1,2,3,…n. The number of ways in which m(≤n) persons can takes seats is:
(a) nPm
(b) nCm X(m–1)!
(c) nCm Xm!
(d) n–1Pm–1
Answer
A,C
Question. The number of ways in which 10 candidates A1, A2,…, A10 can be ranked, so that A1 is always above A2 is:
(a) 10!/2
(b) 8!X10C2
(c) 10P2
(d) 10P2
Answer
A,B
Question. If n and r are two positive integers such that n ≥ r, then nCr-1 + nCr=?
(a) nCn-r
(b) nCr
(c) n-1Cr
(d) n+1Cr
Answer
D
Question. In an election there are 8 candidates, out of which 5 are to be choosen. If a voter may vote for any number of candidates but not greater than the number to be choosen, then in how many ways can a voter vote:
(a) 216
(b) 114
(c) 218
(d) None of these
Answer
C
Question. To fill 12 vacancies there are 25 candidates of which five are from scheduled caste. If 3 of the vacancies are reserved for scheduled caste candidates while the rest are open to all, then the number of ways in which the selection can be made:
(a) 5C3 x 22C9
(b) 22C9 x 5C3
(c) 22C3 + 5C3
(d) None of these
Answer
A
Question. There are 9 chairs in a room on which 6 persons are to be seated, out of which one is guest with one specific chair.
In how many ways they can sit:
(a) 6720
(b) 60480
(c) 30
(d) 346
Answer
A
Question. The number of ways in which 10 persons can go in two boats so that there may be 5 on each boat, supposing that two particular persons will not go in the same boat is
(a) 1/2(10C5)
(b) 2(8C4)
(c) 1/2(8C5)
(d) None of these
Answer
B
Question.
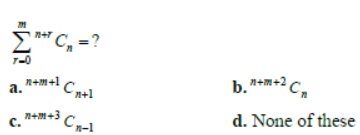
Answer
A
Question. A father with 8 children takes them 3 at a time to the Zoological gardens, as often as he can without taking the same 3 children together more than once. The number of times he will go to the garden is:
(a) 336
(b) 112
(c) 56
(d) None of these
Answer
C
Question. There are four balls of different colours and four boxes of colurs same as those of the balls. The number of ways in which the balls, one in each box, could be placed such that a ball doesn’t go to box of its own colour is:
(a) 8
(b) 7
(c) 9
(d) None of these
Answer
C
Question. Out of 18 points in a plane, no three are in the same straight line except five points which are collinear. The number of:
(i) Straight lines
(a) 140
(b) 142
(c) 144
(d) 146
Answer
C
Question. Triangles which can be formed by joining them
(a) 816
(b) 806
(c) 800
(d) 750
Answer
D
Question. In a city no two persons have identical set of teeth and there is no person without a tooth. Also no person has more than 32 teeth. If we disregard the shape and size of tooth and consider only the positioning of the teeth, then the maximum population of the city is:
(a) 232
(b) (32)2−1
(c) 232 −1
(d) 232-1
Answer
C
Question. If 10Cr = 10Cr+2 , then 5Cr equals ?
(a) 120
(b) 10
(c) 360
(d) 5
Answer
D
Question. The number of diagonals in a octagon will be:
(a) 28
(b) 20
(c) 10
(d) 16
Answer
B
Question. How many triangles can be formed by joining four points on a circle?
(a) 4
(b) 6
(c) 8
(d) 10
Answer
A
Question. In a plane there are 10 points out of which 4 are collinear,then the number of triangles that can be formed by joining these points are:
(a) 60
(b) 116
(c) 120
(d) None of these
Answer
B
Question. The straight lines I1 , I2, I3 are parallel and lie in the same plane. A total number of m points are taken on I1 , n points on I2 , k points on I3 . The maximum number of triangles formed with vertices at these points are:
(a) m+n+kC3
(b) m+n+kC3–mC3–nC3–kC3
(c) mC3+nC3+kC3
(d) None of these
Answer
B
Question. Six points in a plane be joined in all possible ways by indefinite straight lines, and if no two of them be coincident or parallel, and no three pass through the same point (with the exception of the original 6 points). The number of distinct points of intersection is equal to:
(a) 105
(b) 45
(c) 51
(d) None of these
Answer
C
Question. There are n straight lines in a plane, no two of which are parallel and no three pass through the same point. Their points of intersection are joine(d) Then the number of fresh lines thus obtained is:
(a) n(n–1)(n–2)/8
(b) n(n–1)(n–2)(n–3)/6
(c) n(n–1)(n–2)(n–3)/8
(d) None of these
Answer
C
Question. In a plane there are 37 straight lines of which 13 pass through the point A and 11 pass through the point B .
Besides no three lines pass through one point, no line passes through both points A and B and no two are parallel. Then the number of intersection points the lines have is equal to:
(a) 535
(b) 601
(c) 728
(d) None of these
Answer
A
Question. There are 16 points in a plane, no three of which are in a straight line except 8 which are all in a straight line. The number of triangles that can be formed by joining them
equals:
(a) 504
(b) 552
(c) 560
(d) 1120
Answer
A
Question. The number of straight lines that can be formed by joining 20 points no three of which are in the same straight line except 4 of them which are in the same line:
(a) 183
(b) 186
(c) 197
(d) 185
Answer
D
Question. A student is allowed to select utmost n books from a collection of (2n +1) books. If the total number of ways in which he can select one book is 63, then the value of n is:
(a) 2
(b) 3
(c) 4
(d) None of these
Answer
B
Question. The number of ways of painting the faces of a cube with six different colours is:
(a) 1
(b) 6
(c) 6!
(d) 9C2
Answer
A,D
Question. Sanjay has 10 friends among whom two are married to each other. She wishes to invite 5 of the them for a party.
If the married couple refuse to attend separately, the number of different ways in which she can invite five friends is:
(a) 8C5
(b) 2x8C3
(c) 10C5–2 x 8C4
(d) none of these
Answer
B,C
