Students should refer to Worksheets Class 12 Mathematics Application of Derivatives Chapter 6 provided below with important questions and answers. These important questions with solutions for Chapter 6 Application of Derivatives have been prepared by expert teachers for Class 12 Mathematics based on the expected pattern of questions in the class 12 exams. We have provided Worksheets for Class 12 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Application of Derivatives Worksheets Class 12 Mathematics
Question. If the line ax by c + + = 0 is a normal to the curve xy = 1, then
(a) a >0,b< 0
(b) a < 0,b > 0
(c) Both (a) and (b)
(d) None of these
Answer
C
Question. If the line joining the points (0, 3) and 5,-2) ) is a tangent to the curve y=c/x+1′, then the value of c is
(a) 1
(b) -2
(c) 4
(d) None of these
Answer
C
Question. If the subnormal at any point on y=(a-1-nxn is of constant length ,then the value of n is
(a) 1
(b) 0.5
(c) 2
(d) -2
Answer
B
Question. The equation of tangent to the curve (x/a)n+(y/b)n=2at(a ,b) is
(a) x a+ y/b=2
(b) x/a + y/b=1/2
(c) x/b -y/b =2
(d) ax by + = 2
Answer
A
Question. The equation of normal to the curve y=(1+x)v + sin-1(sin2x) at x = 0, is
(a) x+ y = 1
(b) x- y = 1
(c) x+ y = -1
(d) x- y = -1
Answer
A
Question. Two cyclists start from the junction of two perpendicular roads, their velocities being 3v m/min and 4v m/min. The rate at which the two cyclists are separating, is
(a) 7/2 v m/min
(b) 5 v m/min
(c) v m/min
(d) None of these
Answer
B
Question. If the curves x2/a2 + y2/b2 =1 and x2/12-y2/m2=1 cut each other orthogonally, then
(a) a2 +b2 =l2+ m2
(b) a2 – b2= l2– m2
(c) a2 – b2= l2+ m2
(d) a2 + b2=b2 = l2-m2
Answer
C
Question. The point on the curve √x+ √y = 2a2,where the tangent is equally inclined to the axes, is
(a) (a4 , a4)
(b) (0,4a4)
(c) (4a4,0)
(d) None of these
Answer
A
Question. If the area of the triangle, included between the axes and any tangent to the curve xyn=an+1 is constant, then the value of n is
(a) -1
(b) -2
(c) 1
(d) 2
Answer
C
Question. If there is an error of k% in measuring the edge of a cube, then the per cent error in estimating its volume is
(a) k
(b) 3k
(c) k/3
(d) None of these
Answer
B
Question. The interval in which the function f(x) =xe2-x increases, is
(a) (-∞,1)
(b) (2,∞)
(c) (0,2)
(d) None of these
Answer
A
Question. If f (x)x3 + 4x2 +λx+ 1 is a monotonically decreasing function of x in the largest possible interval (-2,-2/3),then
(a) λ = 4
(b)λ = 2
(c) λ = -1
(d) λ has no real value
Answer
A
Question. The value of a for which the function (a+2 )x3-3×2+ 9ax-1decreases monotonically through out for all real x, are
(a) a < – 2
(b) a > – 2
(c) – 3 < a <0
(d) -∞< a ≤-3
Answer
D
Question.
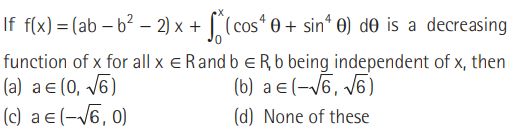
Answer
B
Question. From mean value theorem, f (b)- f(a)f’ (a) ;a≤x1<b,if f(x)=1/x’ , then x1 is equal to
(a) √ab
(b) a+ b/2
(c) 2ab/a +b
(d) b- a/b+ a
Answer
A
Question. Let f (x) be differentiable ∀x. If f(1) = -2 and f’ (x)≥ 2 ∀ x ∈ [1,6] then
(a) f(6)< 8
(b) f(6)≥8
(c) f(6) ≥ 5
(d) f(6) ≤ 5
Answer
B
Question.
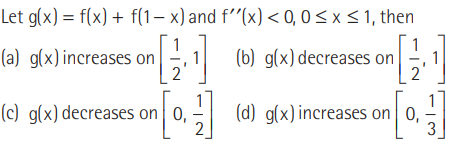
Answer
B
Question. A balloon, which always remains spherical, has a variable diameter 3/2(2x+1). The rate of change of its volume with respect to x, is
(a) 27π/8(2x+1)2
(b) 8π/27(2x+1)2
(c) 27π/8(x+2)2
(d) 8π/27(x+2)2
Answer
A
Question. Sand is pouring from a pipe at the rate of 12 cm 3/s.
The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the base. How fast height of the sand cone increasing when the height is 4/1 cm?
(a) π/48 cm/s
(b) 1/48π cm/s
(c) 48/π cm/s
(d) 48π cm/s
Answer
B
Question. The total revenue in rupees received from the sale of x units of a product is given by R (x) =13x2+ 26x +15.
The marginal revenue when x = 7 is
(a) R.s.197
(b) R.s.199
(c) R.s.205
(d) R.s.208
Answer
D
Question. The total cost C(x) in rupees associated with the production of x units of an item is given by c(x) = 0.007x3 – 0.003x2 + 15x+4000.
The marginal cost when x = 17 units are produced is
(a) R.s.19.196
(b) R.s.20.225
(c) R.s.20.967
(d) R.s.21.297
Answer
C
Question. The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm/s. How fast is the area decreasing when the two equal sides are equal to the base?
(a) 3 b cm2/s
(b) √2 b cm2/s
(c) b/√2 cm2/s
(d) √3 b cm2/s
Answer
D
Question. The rate of change of the surface area of a sphere of radius r, when the radius is increasing at the rate of 2 cm/s is proportional to
(a) 1/r
(b) 1/r2
(c) r
(d) r2
Answer
C
Question. A kite is moving horizontally at a height of 151.5 m.
If the speed of kite is 10 m/s, how fast is the string being let out, when the kite is 250 m away from the boy who is flying the kite? The height of boy is 1.5 m.
(a) 8 m/s
(b) 12 m/s
(c) 16 m/s
(d) 19 m/s
Answer
A
Question. An angle θ, 0<θ<π/2, which increases twice as fast as its sine, is
(a) π/2
(b) 3π/2
(c) π/4
(d) π/3
Answer
D
Question. Moving along the x-axis there are two points with x=10 +6t,x=3+ t2. The speed with which they are reaching from each other at the time of encounter is (x is in centimetre and t is in seconds)
(a) 16 cm/s
(b) 20 cm/s
(c) 8 cm/s
(d) 12 cm/s
Answer
C
Question. The sides of an equilateral triangle are increasing at the rate of 2 cm/s. The rate at which the area increases, when the side is 10 cm, is
(a) √3cm2/s
(b) 10cm2/s
(c) 10 √3cm2/s
(d) 10/√3 cm2/s
Answer
C
Question. If the volume of a sphere is increasing at a constant rate, then the rate at which its radius is increasing, is
(a) a constant
(b) proportional to the radius
(c) inversely proportional to the radius
(d) inversely proportional to the surface area
Answer
D
Question. Gas is being pumped into a spherical balloon at the rate of 30 ft3/min. Then, the rate at which the radius increases when it reaches the value 15 ft, is
(a) 1/30π ft/min
(b) 1/15π ft/min
(c) 1/20 ft/min
(d) 1/15 ft/min
Answer
A
Question. If the radius of a sphere is measured as 7 m with an error of 0.02 m, then the approximate error in calculating its volume is
(a) 3.12 π m3
(b) 3.92π m3
(c) 3.56 π m3
(d) 4.01π m31
Answer
B
Question. An object is moving in the clockwise direction around the unit circle x2 +y2 = 1. As it passes through the point (1/2,√3/2), its y-coordinate is decreasing at the rate of 3 units per second. The rate at which the x-coordinate changes at this point is (in unit per second)
(a) 2
(b) 3√3
(c) √3
(d) 2√3
Answer
B
Question. The position of a point in time ‘ t’ is given by x=a + bt-ct2 , y= at+bt2. Its acceleration at time ‘t ’ is
(a) b- c
(b) b+ c
(c) 2b -2c
(d) 2√b2+c2
Answer
D
Question. At what point on the curve x3-8a2 y=0, the slope of the normal is −2/3 ?
(a) ( a, a)
(b) (2a ,a)
(c) (2a,a)
(d) None of these
Answer
C
Question. The point (s) on the curve y3+3x2= 12y, where the tangent is vertical (parallel to y-axis), is (are)
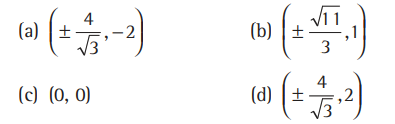
Answer
D
Question. If the tangent at (x1,y1) to the curve x3 + y3 = a3 meets the curve again at (x2,y2), then
(a) x2/x1 + y2/y1 =-1
(b) x2/y1 + x2/y2 =-1
(c) x1/x2 + y1/y2 =-1
(d) x2/x1 + y2/y1 =1
Answer
A
Question. If y=4x-5 is tangent to the curve y2= px3+q at(2,3), then (p ,q) is
(a) (2,7)
(b) −2,7)
(c) (−2,−7)
(d) (2,−7)
Answer
D
Question. The triangle formed by the tangent to the curve f(x) =x2 + bx-b at the point (1, 1) and the coordinate axes, lies in the first quadrant. If its area is 2, then the value of b is
(a) − 1
(b) 3
(c) − 3
(d) 1
Answer
C
Question. The condition for the curves x2/a2 – y2/b2=1,xy= c2 to intersect orthogonally, is
(a) a2 + b2 = 0
(b) a2-b2 = 0
(c) a= b
(d) None of these
Answer
D
Question. y= log(1+x) – 2x/2+x, x>-1, is an increasing function of x throughout in,
(a) x > −1
(b) x > 1
(c) x < 0
(d) x > 0
Answer
A
Question. The angle between the curves y = sin x and y = cos x is

Answer
A
Question. The least value of a such that the function f given by f (x)=x2 + ax+1 is strictly increasing on (1, 2) is
(a) –2
(b) –1
(c) 0
(d) 2
Answer
A
Question. The function xx is increasing, when
(a) x>1/e
(b) x<1/e
(c) x < 0
(d) for all real x
Answer
A
Question. Let f be a function defined on [a, b] such that f (x) > 0, for all x ∈[a ,b ]. Then, f is an increasing function on
(a) (a, b)
(b) (a, b]
(c) [a, b]
(d) [ a ,b)
Answer
A
Question. Water is dripping out from a conical funnel of semi-vertical angle π/4 at the uniform rate of 2 cm2/s in the surface area, through a tiny hole at the vertex of the bottom. When the slant height of cone is 4 cm, the rate of decrease of the slant height of water, is
(a) √2/4π cm/s
(b) 1/4π cm/s
(c) 1/π √2 cm/s
(d) None of these
Answer
A