Class 9 Triangles Worksheet PDF have been designed as per the latest pattern for CBSE, NCERT and KVS for Grade 9. Students are always suggested to solve printable worksheets for Mathematics Triangles Grade 9 as they can be really helpful to clear their concepts and improve problem solving skills. We at worksheetsbag.com have provided here free PDF worksheets for students in standard 9 so that you can easily take print of these test sheets and use them daily for practice. All worksheets are easy to download and have been designed by teachers of Class 9 for benefit of students and is available for free download.
Mathematics Triangles Worksheets for Class 9
We have provided chapter-wise worksheets for class 9 Mathematics Triangles which the students can download in Pdf format for free. This is the best collection of Mathematics Triangles standard 9th worksheets with important questions and answers for each grade 9th Mathematics Triangles chapter so that the students are able to properly practice and gain more marks in Class 9 Mathematics Triangles class tests and exams.
Chapter-wise Class 9 Mathematics Triangles Worksheets Pdf Download
1. Congruence of Triangles
2. Criteria for Congruence of Triangles
3. Some Properties of a Triangle
4. Inequalities in a Triangle
• Triangle – A closed figure formed by three intersecting lines is called a triangle. A triangle has three sides, three angles and three vertices.
·• Congruent figures – Congruent means equal in all respects or figures whose shapes and sizes are both the same for example, two circles of the same radii are congruent. Also two squares of the same sides are congruent.
• Congruent Triangles- two triangles are congruent if and only if one of them can be made to superpose on the other, so as to cover it exactly.
• If two triangles ABC and PQR are congruent under the correspondence A ↔ P,B ↔ Q and C ↔ R then symbolically, it is expressed as DABC ≅ DPQR
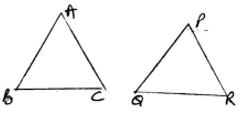
• In congruent triangles corresponding parts are equal and we write ‘CPCT’ for corresponding parts of congruent triangles.
·• SAS congruency rule – Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle. For example: ΔABC and ΔPQR as shown in the figure satisfy SAS congruent criterion
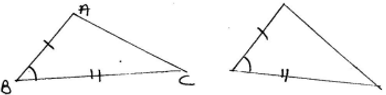
• ASA Congruence Rule – Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle. For examples ΔABC and ΔDEF shown below satisfy ASA congruence criterion.

• AAS Congruence Rule – Two triangle are congruent if any two pairs of angles and one pair of corresponding sides are equal for example ΔABC and ΔDEF shown below satisfy AAS congruence criterion.
• AAS criterion for congruence of triangles is a particular case of ASA criterion.
• Isosceles Triangle – A triangle in which two sides are equal is called an isosceles triangle.
For example: DABC shown below is an isosceles triangle with AB=AC.
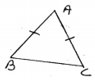
• Angle opposite to equal sides of a triangle are equal.
• Sides opposite to equal angles of a triangle are equal.
• Each angle of an equilateral triangle is 60o .
• SSS congruence Rule – If three sides of one triangle are equal to the three sides of another triangle then the two triangles are congruent for example ΔABC and ΔDEF as shown in the figure satisfy SSS congruence criterion.
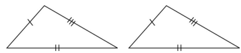
• RHS Congruence Rule – If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle then the two
triangle are congruent. For example: ΔABC and ΔPQR shown below satisfy RHS congruence criterion.

RHS stands for right angle – Hypotenuse side.
• A point equidistant from two given points lies on the perpendicular bisector of the line segment joining the two points and its converse.
• A point equidistant from two intersecting lines lies on the bisectors of the angles formed by the two lines.
• In a triangle, angle opposite to the longer side is larger (greater)
• In a triangle, side opposite to the large (greater) angle is longer.
• Sum of any two sides of a triangle is greater than the third side.
1. Which of the following is not a criterion for congruence of triangles?
(A) SAS
(B) ASA
(C) SSA
(D) SSS
Answer
C
2. If AB = QR, BC = PR and CA = PQ, then
(A) ΔABC ≅ ΔPQR
(B) ΔCBA ≅ ΔPRQ
(C) ΔBAC ≅ ΔRPQ
(D) ΔPQR ≅ ΔBCA
Answer
B
3. In ΔABC, AB = AC and ∠B = 50°. Then ∠C is equal to
(A) 40°
(B) 50°
(C) 80°
(D) 130°
Answer
B
4. In ΔABC, BC = AB and ∠B = 80°. Then ∠A is equal to
(A) 80°
(B) 40°
(C) 50°
(D) 100°
Answer
C
5. In ΔPQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is
(A) 4 cm
(B) 5 cm
(C) 2 cm
(D) 2.5 cm
Answer
A
6. D is a point on the side BC of a ΔABC such that AD bisects ∠BAC. Then
(A) BD = CD
(B) BA > BD
(C) BD > BA
(D) CD > CA
Answer
B
7. It is given that ΔABC ≅ ΔFDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
(A) DF = 5 cm, ∠F = 60°
(B) DF = 5 cm, ∠E = 60°
(C) DE = 5 cm, ∠E = 60°
(D) DE = 5 cm, ∠D = 40°
Answer
B
8. Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be
(A) 3.6 cm
(B) 4.1 cm
(C) 3.8 cm
(D) 3.4 cm
Answer
D
9. In Δ PQR, if ∠R > ∠Q, then
(A) QR > PR
(B) PQ > PR
(C) PQ < PR
(D) QR < PR
Answer
B
10. In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are
(A) isosceles but not congruent
(B) isosceles and congruent
(C) congruent but not isosceles
(D) neither congruent nor isosceles
Answer
A
11. In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom. Then,
(A) BC = EF
(B) AC = DE
(C) AC = EF
(D) BC = DE
Answer
B
1. In triangles ABC and PQR, ∠A= ∠Q and ∠B = ∠R. Which side of ΔPQR should be equal to side AB of ΔABC so that the two triangles are congruent? Give reason for your answer.
Sol.

In triangle ABC and PQR, we have
∠A = ∠Q [Given]
∠B = ∠R [Given]
For the triangle to be congruent, we must AB = QR. They will be congruent by ASA congruence rule.
2. In triangles ABC and PQR, ∠A= ∠Q and ∠B = ∠R. Which side of ΔPQR should be equal to side BC of ΔABC so that the two triangles are congruent? Give reason for your answer.
Sol.
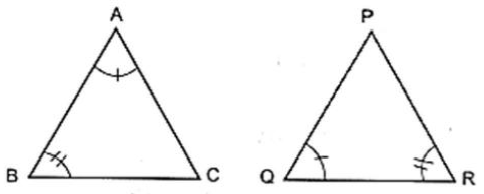
In triangle ABC and PQR, we have
∠A = ∠Q and ∠B = ∠R [Given]
For the triangles to be congruent, we must have
BC = RP
They will be congruent By AAS congruence rule.
3. “If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Sol. This statement is not true. Angles must be the included angles.
4. “If two angles and a side of one triangle are equal to two angles and a side of
another triangle, then the two triangles must be congruent.” Is the statement true?
Why?
Sol. This statement is true. Sides must be corresponding sides.
5. Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
Sol. We know that the sum of any two sides of a triangle is always greater than the third side.
Here, the sum of two sides whose lengths are
4 cm and 3 cm = 4 cm + 3 cm = 7 cm,
Which is equal to the length of third side, i.e., 7 cm.
Hence, it is not possible to construct a triangle with lengths of sides 4 cm, 3 cm and 7 cm.
6. It is given that ΔABC ≅ ΔRPQ. Is it true to say that BC = QR? Why?
Sol. It is False that BC = QR because BC = PQ as ΔABC ≅ ΔRPQ.
7. It is given that ΔPQR ≅ ΔEDF, then is it true to say that PR = EF? Give reason for your answer.
Sol. Yes, PR = EF because they are the corresponding sides of ΔPQR and ΔEDF.
8. In ΔPQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is the longest? Give reason for your answer.
Sol. In ΔPQR, we have
∠Q =1800 − (∠P +∠R)
= 1800 − (700 + 300) = 1800 − 1000 = 800
Now, in ΔPQR, ∠Q is the larger (greater) and side opposite to greater angle is longer.
Hence, PR is the longest side.
9. AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2 AD? Give reason for your answer.
Sol. In ΔABD, we have

AB + BD > AD …(1)
[∵ Sum of the lengths of any two sides of a triangle must be greater than the third sides]
Now, in ΔADC, we have
AC + CD > AD …(2)
[∵Sum of the lengths of any two sides of a triangle must be greater that the third side]
Adding (1) and (2), we get
AB + BD + CD + AC > 2AD
⇒AB + BC +CA > 2AD [∵BD = CD as AD is median of ΔABC]
10. M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
Sol. We have to prove that
AB + BC + AC > 2AM.
As sum of any two sides of a triangle is greater than the third side, so in ΔABM, we have
AB + BM > AM …(1)
And in ΔACM, AC + CM > AM …(2)
Adding (1) and (2), we get
AB + BM + AC + CM > 2AM
Or AB + (BM + CM) + AC > 2AM
⇒ AB + BC + AC > 2AM
Hence, it is true to say that perimeter of the triangle is greater than 2AM.
11. Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
Sol. No, it is not possible to construct a triangle whose sides are 9cm, 7cm and 17cm because 9cm + 7cm = 16cm < 17cm Whereas sum of any two sides of a triangle is always greater than the third side.
12. Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
Sol. Yes, it is possible to construct a triangle with lengths of sides as 8 cm, 7 cm and 4 cm as sum of any two sides of a triangle is greater than the third side.
1. ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
Sol. Given: ΔABC with AB = AC
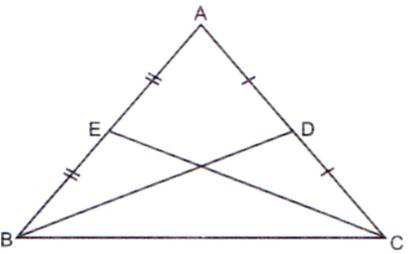
And AD = CD, AE = BE.
To prove: BD = CE
Proof: In DABC we have
AB = AC [Given]
⇒ (1/2)AB = (1/2)AC
⇒ AE = AD
[∵ D is the mid-point of AC and E is the mid-point of AB]
Now, in ΔABD and ΔACE, we have
ΔABD ≅ ΔACE
⇒ BD = CE [CPCT]
Hence, proved.
2. In Fig .7.4, D and E are points on side BC of a Δ ABC such that BD = CE and AD = AE. Show that Δ ABD ≅ Δ ACE.

Sol. Given: ΔABC in which BD = CE and AD = AE.
To Prove: ΔABD ≅ ΔACE
Proof: In ΔADE, we have
AD = AE [Given]
⇒ ∠2 = 1
[∵Angle opposite to equal sides of a triangle are equal]
Now, ∠1+∠3 =180 …(1)
[Linear pair axiom]
∠2 +∠4 =180 …(2)
[Linear pair axiom]
From equations (1) and (2), we get
∠1+ ∠3 = ∠2 +∠4
⇒ ∠3 = ∠4 [∵∠1= ∠2]
Now, in ΔABD and ΔACE, we have
AD = AE [Given]
∠3 = ∠4 [Proved above]
BD = CE [Given]
So, by SAS criterion of congruence, we have
ΔABD ≅ ΔACE
Hence, proved
3. CDE is an equilateral triangle formed on a side CD of a square ABCD (Fig.7.5). Show that ΔADE ≅ ΔBCE.

Sol. Given: An equilateral triangle CDE formed on side CD of square ABCD.
To prove: ΔADE ≅ ΔBCE
Proof: In square ABCD, we have
∠1 = ∠2 …(1) [∵Each = 90o]
Now, in ΔDCE, we have
∠3 = ∠4 …(2) [∵Each = 60o]
Adding (1) and (2), we get
∠1+ ∠3 = ∠2 +∠4
⇒ ∠ADE + ∠BCE
Now, in ΔADE and ΔBCE, we have
DE = CE [Sides of an equilateral triangle are equal]
∠ADE = ∠BCE [Hence proved]
AD = BC [Sides of a square are equal in length]
So, by SAS criterion of congruence, we have
ΔADE ≅ ΔBCE
Hence, proved
4. In Fig.7.6, BA ⊥ AC, DE ⊥DF such that BA = DE and BF = EC. Show that Δ ABC ≅ Δ DEF.

Sol. We have BF = EC
∴ BF + FC = CE + FC ⇒ BC = EF
In ΔABC, ∠A = 900 and in ΔDEF,ÐD = 900 .
∴ ΔABC and ΔDEF are right triangles.
Now, in right triangles ABC and DEF, we have
BA = DE [Given]
And BC = EF [Proved above]
∴ ΔABC ≅ ΔDEF [By RHS congruence rule]
5. O is a point on the side SR of a ΔPSR such that PQ = PR. Prove that PS > PQ.
Sol. Given: PQ = PR
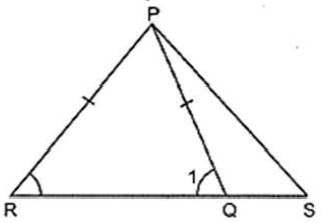
To prove: PS > PQ
Proof: In ΔPRQ, we have
PR = PQ [Given]
⇒ ∠1 = ∠R
[∵Angles opposite to equal side of triangle are equal]
But, ∠1 > ∠S
[∵Exterior angle of a triangle is greater than each of the remote
interior angles]
⇒ ∠R > ∠S [∵∠1= ∠R]
⇒ PS < PR [∵ In a triangle, side opposite to the large is longer]
Hence, proved.
6. S is any point on side QR of a ΔPQR. Show that: PQ + QR + RP > 2 PS.
Sol. Given: A Point S on side QR of ΔPQR.

To prove: PQ + QR + RP > 2PS
Proof: In ΔPQS, we have
PQ + QS > PS …(1)
[∵ Sum of the length of any two sides of a triangle must be greater than the third side]
Now, in ΔPSR, we have
RS + RP > PS …(2)
[∵ Sum of the length of any two sides of triangle must be greater than the third side]
Adding (1) and (2), we get
PQ + QS + RS + RP > 2PS
⇒ PQ + QR + RP > 2PS
Hence, proved.
7. D is any point on side AC of a ΔABC with AB = AC. Show that CD < BD.
Sol. In ΔABC, we have
AB = AC [Given]
∴ ∠ABC = ∠ACB
[∵ Angles opp. To equal sides of a triangle are equal]
Now, ∠DBC < ∠ABC
∴ ∠DBC < ∠ACB or ∠DBC < ∠DCB
Hence, CD > BD. [∵ Side opposite a greater angle is longer]
8. In Fig. 7.7, l||m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.
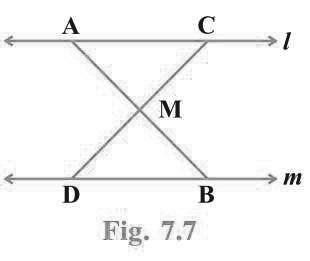
Sol. In ΔAMC and ΔBMD, we have
∠1 = ∠3 [Alt. ∠s because l||m]
∠2 = ∠4 [Vert. opp. ∠s ]

AM = BM [Given]
∴ DAMC ≅ DBMD [By ASS congruence rule]
∴ CM = DM [CPCT]
Hence, M is also the mid-point of CD.
9. Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
Sol. Bisector of the angles B and C of an isosceles triangle ABC and AB = AC intersect each other at O. BO is produced to a point M.
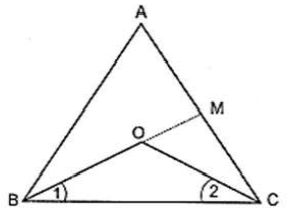
In ΔABC, we have
AB = AC
∴ ∠ABC = ∠ACB
[∵Angles opposite to equal sides of a triangle are equal]
⇒ 1/3 ∠ABC = 1/2 ∠ACB
i.e., ∠1 = ∠2 [∵BO and CO are bisectors of ∠B and ∠C ]
In ΔOBC, Ext. ∠MOC = ∠1+ ∠2
[∵ Exterior angle of a triangle is equal to the sum of interior opposite angles]
⇒ Ext. ∠MOC = 2∠1
Hence, ∠MOC = ∠ABC.
10. Bisectors of the angles B and C of an isosceles triangle ABC with AB = AC intersect each other at O. Show that external angle adjacent to ∠ABC is equal to ∠BOC.
Sol. In ΔABC we have
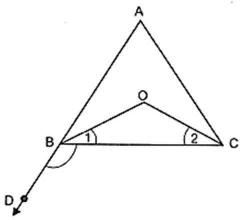
AB = AC
∴ ∠B = ∠C [∵Angles opposite to equal sides of a triangle are equal]
∴ 1/2 ∠B = 1/2 ∠C …(1)
In ΔOBC,we have
∠ = 1/2 ∠B
And ∠2 = 1/2 ∠C
∴ ∠1 = ∠2 [By (1)]
∠DBC + ∠1 + ∠OBA = 1800 [∵ ABD is a straight line]
⇒ ∠DBC + 2∠1 =1800 [∵ ∠1 = ∠OBA] …(1)
In ΔOBC,
∠1 + ∠2 + ∠BOC = 1800
⇒ 2 ∠1 + ∠BOC = 1800 [∵ ∠1 = ∠2] …(2)
From (1) and (2), we get
∠DBA + 2 ∠1 = 2 ∠1 + ∠BOC
⇒ ∠DBC = ∠BOC
11. In Fig. 7.8, AD is the bisector of ∠BAC. Prove that AB > BD.

Sol. Since exterior angle of a triangle is greater than either of the interior opposite angles, therefore, in ΔACD,
Ext ∠3 > ∠2⇒ ∠3 > ∠1
[∵ AD is the bisector of ∠BAC, so ∠1 = ∠2 ]
Now, in ΔABD, we have
∠3 > ∠1
Hence, AB > BD. [∵ In a triangle, side opposite to greater angle is longer]
1. Find all the angles of an equilateral triangle.
Sol. In ΔABC,we have
AB = AC
⇒ ∠C = ∠B …(1)
[∵ Angles opposite to equal sides of a triangle are equal]
BC = AC
⇒ ∠A = ∠B …(2)
[∵Angles opposite to equal sides of a triangle are equal]
Now, 0 ∠A + ∠B + ∠C = 1800 [∵ Angle sum property of a triangle]
⇒ ∠A+∠A+∠A =1800 [From (1) and (2)]
⇒ 3∠A =1800
⇒ ∠A = 1800/3 = 600
∠A = ∠B = ∠C = 600
2. The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in Fig. 7.12. Prove that the image is as far behind the mirror as the object is in front of the mirror.

Sol. Let AB intersect LM at O. We have to prove that AO = BO.
Now, ∠i = ∠r …(1)
[∵Angle of incidence = Angle of reflection]
∠B = ∠i [Corres. ∠s] …(2)
And ∠A = ∠r [Alternate int. ∠s ] …(3)
From (1), (2) and (3), we get
∠B = ∠A
⇒ ∠BCO = ∠ACO

In ΔBOC and ΔAOC we have
∠1 = ∠2 [Each = 90o]
OC = OC [Common side]
And ∠BCO = ∠ACO [Proved above]
∴ ΔBOC ≅ ΔAOC [ASA congruence rule]
Hence, AO = BO [CPCT]
3. ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD⊥BC (Fig. 7.13). To prove that ∠BAD = ∠CAD, a student proceeded as follows:

In ΔABD and ΔACD,
AB = AC (Given)
∠B = ∠C (because AB = AC)
and ∠ADB = ∠ADC
Therefore, ΔABD = ΔACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
Sol. In ΔABD and ΔADC, we have
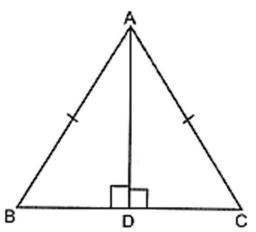
∠ADB = ∠ADC [∵Each equal to 90o]
AB = BC [Given]
AD = AD [Common side]
So, by RHS criterion of congruence, we have
ΔABD ≅ ΔACD
∴ ∠BAD = ∠CAD [CPCT]
Hence, proved.
4. P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
Sol. We have to prove that BPQ is an isosceles triangle.

∠1 = ∠2 …(1)
[∵ BP is the bisector of ∠ABC ]
Now, PQ is parallel to BA and BP cuts them
∴ ∠1 = ∠3 [Alt. ∠s ] …(2)
From (1) and (2), we get
∠2 = ∠3
In ΔBPQ we have
∠2 = ∠3 [Proved above]
∴ PQ = BQ [∵Side of opp. To equal angles are equal]
Hence, BPQ is an isosceles triangle.
5. ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
Sol. In ΔABC and ΔCBD, We

AB = BC [Given]
AD = CD [Given]
BD = BD [Common side]
∴ ΔABC ≅ ΔCBD [By SSS congruence rule]
⇒ ∠1 = ∠2 [CPCT]
And ∠3 = ∠4
Hence, BD bisects both the angle ABC and ADC.
6. ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2 AD.
Sol. Given: A right angles triangle with AB = AC bisector of ∠A meets BC at D.
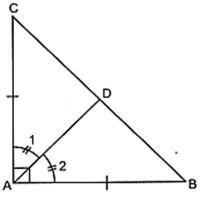
To prove: BC = 2AD
Proof: In right ΔABC,
AB = AC [Given]
⇒ BC is hypotenuse
[ ∵Hypotenuse is the longest side.]
∴ ∠BAC = 900
Now, in ΔCAD and ΔBAD we have
AC = AB [Given]
∠1 = ∠2 [∵AD is the bisector of ∠A]
AD = AD [Common side]
So, By SAS criterion of congruence, we have
ΔCAD ≅ ΔBAD
∴ CD = BD [CPCT]
⇒ AB = BD = CD …(1)
[∵Mid-point of hypotenuse of a rt. D is equidistant from the
three vertices of a D ]
Now, BC = BD + CD
⇒ BC = AD + AD [Using (1)]
⇒ BC = 2AD
Hence, proved.
7. O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that Δ OCD is an isosceles triangle.
Sol. Given: A square of ABCD and OA = OB = AB.

TO prove: ΔOCD is an isosceles triangle.
Proof: In square ABCD,
∠1 = ∠2 …(1)
[∵Each equal to 90o]
Now, in ΔOAB , we have
∠3 = ∠4 …(2)
[∵Each equal to 60o]
Subtracting (2) from (1), we get
∠1−∠3 = ∠2 −∠4
⇒ ∠5 = ∠6
Now, in ΔDAO and ΔCBO,
AD = BC [Given]
∠5 = ∠6 [Proved above]
OA = OB [Given]
So, By SAS criterion of congruence, we have
ΔDAO ≅ ΔCBO
∴ OD = OC
⇒ ΔOCD is an isosceles triangle.
Hence, proved.
8. ABC and DBC are two triangles on the same base BC such that A and D lie on the opposite sides of BC, AB = AC and DB = DC. Show that AD is the perpendicular bisector of BC.
Sol. Given: ΔABC and ΔDBC on the same base BC. Also, AB = AC and BD = DC.
To prove: AD is the perpendicular bisector of BC i.e., OB = OC
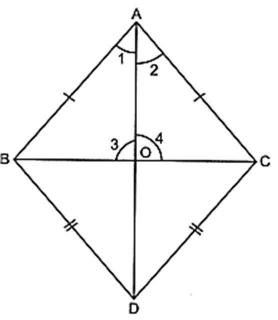
Proof: In ΔBAD and ΔCADwe have
AB = AC [Given]
BD = CD [Given]
AD = AD [Given]
[common side]
So, by SSS criterion of congruence, we have
ΔBAD ≅ ΔCAD
∴ ∠1 = ∠2 [CPCT]
Now, in ΔBAO and ΔCAO, we have
AB = AC [Given]
∠1 = ∠2 [Proved above]
AO = AO [Common side]
So, by SAS criterion of congruence, we have
ΔBAO ≅ ΔCAO
∴ BO = CO [CPCT]
And, ∠3 = ∠4 [CPCT]
But, ∠3+∠4 =1800 [Linear pair axiom]
⇒ ∠3+∠3 =1800
⇒ 2∠3 =1800
⇒ ∠3 = 1800 / 2 = 900
∴ AD is perpendicular bisector of BC [∵BO = CO and ∠3 = 900]
Hence, proved.
9. ABC is an isosceles triangle in which AC = BC. AD and BE are respectively two altitudes to sides BC and AC. Prove that AE = BD.
Sol. In ΔADC and ΔBEC we have

AC = BC [Given] …(1)
∠ADC = ∠BEC [Each = 90o]
∠ACD = ∠BCE [Common angle]
∴ ΔADC ≅ ΔBEC [By SSS congruence rule]
∴ CE = CD [CPCT] …(2)
Subtracting (2) from (1), we get
AC – CE = BC – CD
⇒ AE = BD
Hence, proved.
10. Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
Sol. Given: ΔABC with median AD.
To prove:
AB + AC > 2AD
AB + BC > 2AD
BC + AC > 2AD

Mathematics Triangles Worksheets for Class 9 as per CBSE NCERT pattern
Parents and students are welcome to download as many worksheets as they want as we have provided all free. As you can see we have covered all topics which are there in your Class 9 Mathematics Triangles book designed as per CBSE, NCERT and KVS syllabus and examination pattern. These test papers have been used in various schools and have helped students to practice and improve their grades in school and have also helped them to appear in other school level exams. You can take printout of these chapter wise test sheets having questions relating to each topic and practice them daily so that you can thoroughly understand each concept and get better marks. As Mathematics Triangles for Class 9 is a very scoring subject, if you download and do these questions and answers on daily basis, this will help you to become master in this subject.
Benefits of Free Class 9 Triangles Worksheet PDF
- You can improve understanding of your concepts if you solve NCERT Class 9 Mathematics Triangles Worksheet,
- These CBSE Class 9 Mathematics Triangles worksheets can help you to understand the pattern of questions expected in Mathematics Triangles exams.
- All worksheets for Mathematics Triangles Class 9 for NCERT have been organized in a manner to allow easy download in PDF format
- Parents will be easily able to understand the worksheets and give them to kids to solve
- Will help you to quickly revise all chapters of Class 9 Mathematics Triangles textbook
- CBSE Class 9 Mathematics Triangles Workbook will surely help to improve knowledge of this subject
These Printable practice worksheets are available for free download for Class 9 Mathematics Triangles. As the teachers have done extensive research for all topics and have then made these worksheets for you so that you can use them for your benefit and have also provided to you for each chapter in your ebook. The Chapter wise question bank and revision worksheets can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 9 Mathematics Triangles Worksheets PDF.

You can download free worksheets for Class 9 Mathematics Triangles from https://www.worksheetsbag.com
You can get free PDF downloadable worksheets for Grade 9 Mathematics Triangles from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided worksheets for all subjects in Grade 9, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.worksheetsbag.com without any charge
Yes all test papers for Mathematics Triangles Class 9 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all worksheets.
https://www.worksheetsbag.com is the best portal to download all worksheets for all classes without any charges.