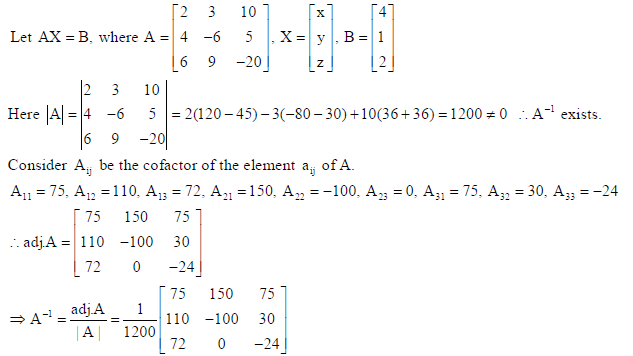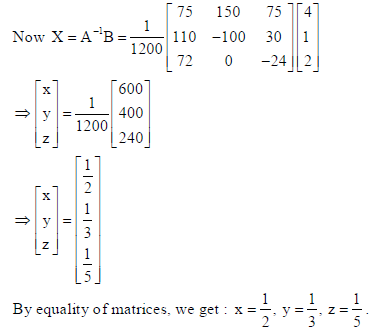Please refer to Class 12 Mathematics Sample Paper Set I with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
SECTION – A
1. Find the angle between the line r̅ = (2î − ĵ+ 3k̂ ) + λ(3î − ĵ+ 2k̂ ) and the plane r̅.(î + ĵ+ k̂) = 3.
Sol.

OR
Find the coordinates of the point, where the line
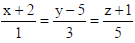
cuts the yz-plane.
Sol. Coordinates of random point on the line is (λ − 2, 3λ + 5, 5λ −1) .
As the line cuts yz-plane (whose equation is x = 0 ) so, λ − 2 = 0 ⇒ λ = 2 .
Therefore the required point is (0, 11, 9).
2.
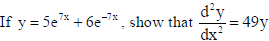
Sol.
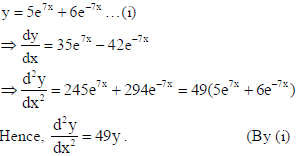
3. If A is a square matrix of order 2 and |A| = 4 , then find the value of |2AA’| , where A’ is the transpose of matrix A.
Sol. |2AA’| = 22 |AA’| = 4 |A||A’| = 4|A||A| = 4×4×4 = 64 .
4. Find the order of the differential equation of the family of circles of radius 3 units.
Sol. Let the equation of circle be (x − h)2 + (y − k)2 = 32 , where (h, k) is the centre.
∵ there are two arbitrary constants h and k in the equation given above so, Order of the corresponding Differential Equation must be 2.
SECTION – B
5. Find the value of (x – y) from the matrix equation
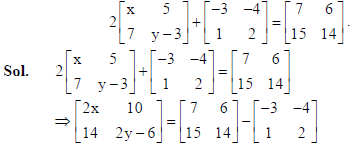
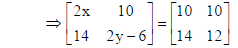
By equality of matrices, we get : 2x =10, 2y − 6 =12 ⇒ x = 5, y = 9 .
∴ x − y = 5− 9 = −4 .
6. Solve the following differential equation :
(y + 3x2) dx/dy = x
Sol.
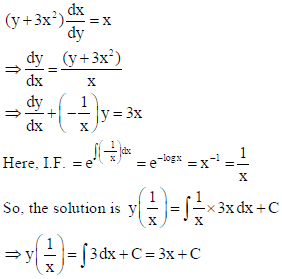
That is, y = 3x2 + xC .
7. Find : ∫ex (cos x − sin x) cosec2x dx .
Sol. ∫ex (cos x − sin x) cosec2x dx
⇒ = ∫ex [(−cosec x) + cot x cosec x]dx
⇒ = ex (−cosec x) + C
Note that, ∫ex [f (x) + f'(x)]dx = ex ×f (x) + C.
8. Using vectors, prove that the points (2, –1, 3), (3, –5, 1) and (–1, 11, 9) are collinear.
Sol. Let A(2, –1, 3), B(3, –5, 1) a̅nd C(–1, 11, 9).
Here A̅B̅ = î − 4ĵ − 2k̂, A̅C̅ = −3î + 12ĵ + 6k̂
∵ A̅C̅ = −3A̅B̅ ∴ A̅C̅||A̅B̅
But A is a common point so, A, B and C are collinear.
OR
For any two vectors a̅ and b̅, prove that
(a̅ × b̅)2 a̅2 b̅2 − (a̅ .b̅)2.
Sol. Consider (a̅ × b̅)2 ={|a̅||b̅ |sinθn}2
⇒ |a̅|2|b̅|2 sin2θ
⇒ |a̅|2|b̅|2 (1−cos2θ)
⇒ |a̅|2|b̅|2 − |a̅|2|b̅|2 cos2θ
⇒ |a̅|2|b̅|2 − {|a̅|2|b̅|2cos2θ}
∴ (a̅ × b̅)2 = a̅2b̅2 − (a̅ .b̅)2
9. Find :
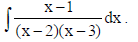
Sol.
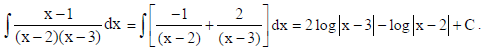
OR
Integrate :
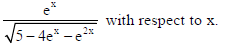
Sol. Put ex = t ⇒ exdx = dt
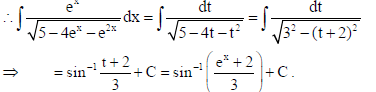
10. If P(A) = 0.6, P(B) = 0.5 and P(B|A) = 0.4, find P(A ∪ B) and P(A|B).
Sol. As P(B∩A) = P(B|A)× P(A) = 0.4×0.6 = 0.24
That is, P(A∩B) = 0.24
Now P(A|B) = P(A∩B)/P(B) = 0.24/0.5 = 24/50 = 0.48
Also, P(A∪B) = P(A) + P(B) − P(A∩B) = 0.6 + 0.5− 0.24 = 0.86 .
11. If an operation * on the set of integers Z is defined by a *b = 2a2 + b , then find (i) whether it is a binary or not, and (ii) if a binary, then is it commutative or not.
Sol. (i) As a2 ∈ Z ∴ 2a2 + b ∈ Z for all a, b ∈ Z
That is, a *b ∈ Z so, is binary.
(ii) Note that 1*2 = 2×12 + 2 = 4 and 2*1 = 2×22 +1 = 9 i.e., 1*2 ≠ 2*1
Therefore, * isn’t commutative.
12. Four cards are drawn one by one with replacement from a well-shuffled deck of playing cards.
Find the probability that at least three cards are of diamonds.
Sol.
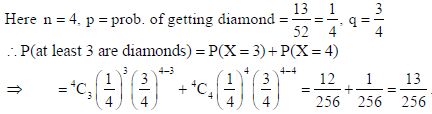
OR
The probability of two students A and B coming to school on time are 2/7 and 4/7, respectively. Assuming that the events ‘A coming on time’ and ‘B coming on time’ are independent, find the probability of only one of them coming to school on time.
Sol. Let E1 : A coming on time and E2 : B coming on time.
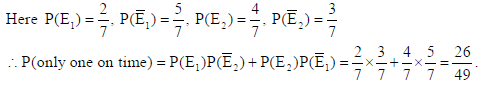
SECTION – C
13.
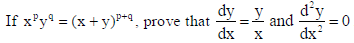
Sol. Here xpyq = (x + y)p+q
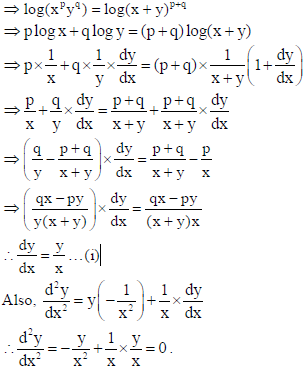
14. Find : ∫(sin x.sin 2x.sin 3x)dx .
Sol.
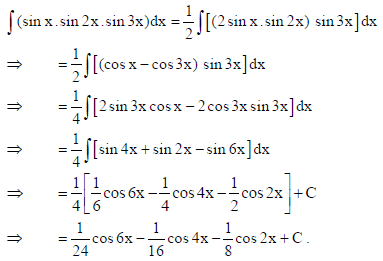
15. Differentiate
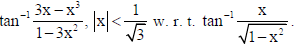
Sol.
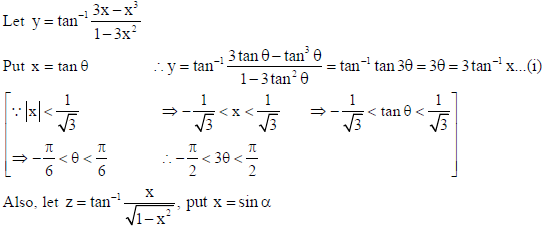
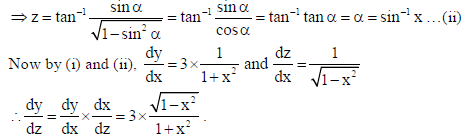
OR
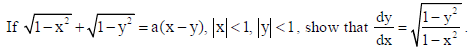
Sol.
16. Find the particular solution of the differential equation :
(1+ e2x )dy + (1+ y2 )exdx = 0, given that y(0) =1.
Sol.
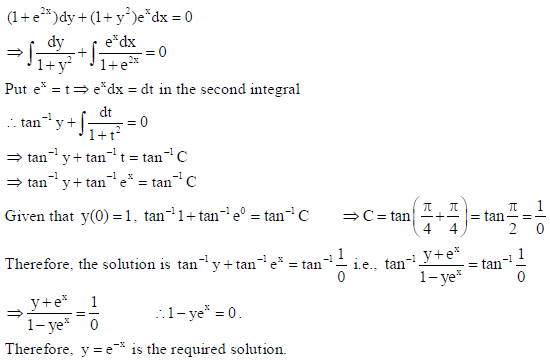
OR
Find the particular solution of the differential equation :
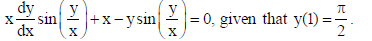
Sol.
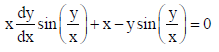

17. Prove that the relation R in the set A = {1, 2, 3, 4, 5, 6, 7} given by
R = {(a, b) : |a − b| is even} is an equivalence relation .
Sol. Reflexive : ∵ |a − a| = 0 which is even ∴(a,a) ∈ R .
So, R is reflexive.
Symmetric : Let (a, b) ∈ R implies |a − b| is even which means |b − a| is also even .
That means, (b,a) ∈ R . Therefore, R is symmetric.
Transitive : Let (a, b) ∈ R, (b,c) ∈ R .
It means |a − b| and |b − c| are even.
That is, |a − b| = 2m, |b − c| = 2n, where m,n ∈ Z
⇒a − b = ±2m, b − c = ±2n
⇒a − b + b − c = a − c = ±2(m+ n)
⇒ a − c = 2(m+ n) , i.e., a − c is even.
That is, (a,c) ∈ R . So, R is transitive.
Hence R is equivalence relation.
Show that the function f in A=R −{2/3} defined as f (x) = 4x+3/6x−4 is one-one and onto.
Hence, find f–1.
Sol.
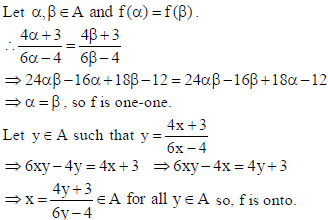
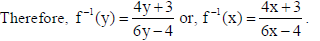
18. Find whether the function f (x) = (cos 2x + π/4), is increasing or decreasing in the interval
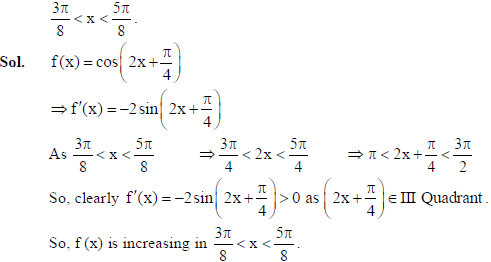
19. Find the equation of the plane passing through the point (–1, 3, 2) and perpendicular to the planes x + 2y + 3z = 5 and 3x + 3y + z = 0 .
Sol. Let A, B, C be the d.r.’s of normal to the required plane.
So, A(x +1) + B(y −3) + C(z − 2) = 0…(i)
As (i) is perpendicular to the planes x + 2y + 3z = 5 and 3x + 3y + z = 0 so,
A + 2B + 3C = 0…(ii)
3A + 3B + C = 0…(iii)
Solving (ii) and (iii), we get : A/−7 = B/8 = C/−3 i.e., the d.r.’s are 7, –8, 3.
By (i), 7(x +1) −8(y −3) + 3(z − 2) = 0 i.e., 7x −8y + 3z + 25 = 0 .
20. Prove that :
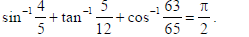
Sol.
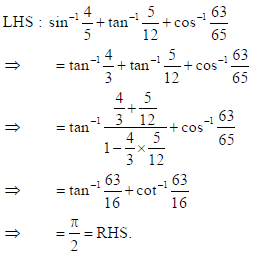
21. Evaluate :
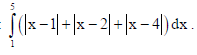
Sol.
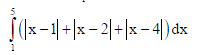
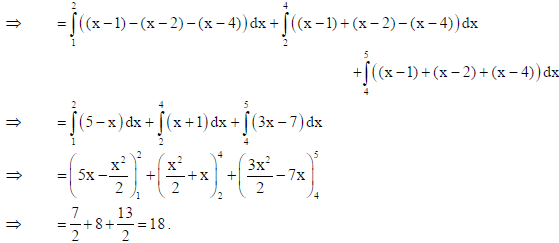
22. Using vectors, find the value of x such that the four points A(x, 5, –1), B(3, 2, 1), C(4, 5, 5) and D(4, 2, –2) are coplanar.
Sol.
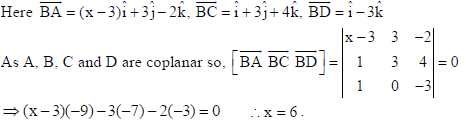
23.
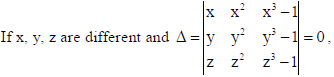
then using properties of determinants, show that xyz =1.
Sol.

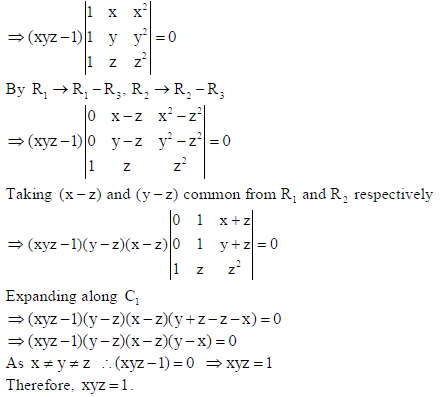
SECTION – D
24. Using integration, find the area of the following region :
{(x, y) : x2 + y2 ≤ 16a2 and y2 ≤ 6ax}
Sol.

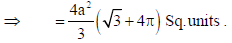
OR
Using integration, find the area of triangle ABC bounded by the lines 4x − y + 5 = 0, x + y − 5 = 0 and x − 4y + 5 = 0 .
Sol.
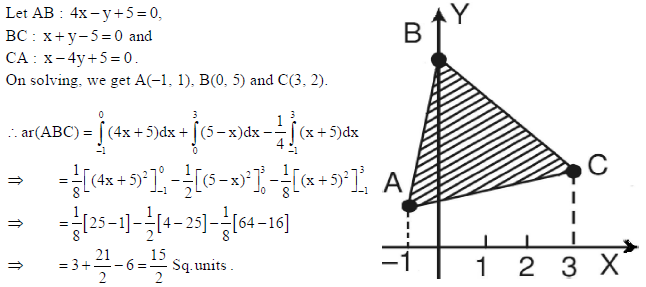
25. Find the vector equation of the line passing through (2, 1, –1) and parallel to the line r̅ = (î + ĵ) + λ(2î − ĵ+ k̂) . Also, find the distance between these two lines.
Sol.
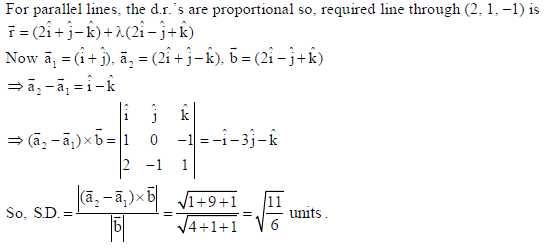
OR
Find the coordinates of the foot Q of the perpendicular drawn from the point P(1, 3, 4)
to the plane 2x − y + z + 3 = 0 . Find the distance PQ and the image of P treating the plane as a
mirror.
Sol.
26. A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours and 20 minutes available for cutting and 4 hours available for assembling.
The profit for type A souvenirs is Rs 100 each and for type B souvenirs, profit is Rs 120 each. How many souvenirs of each type should the company manufacture in order to maximize the profit ? Formulate the problem as a LPP and then solve it graphically.
Sol. Let the number of Souvenirs of type A and type B be x and y, respectively.
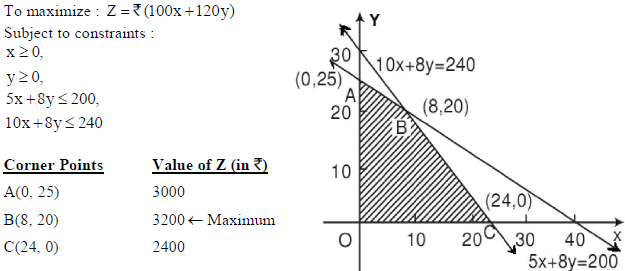
Hence maximum profit of Rs 3200 is obtained when 8 souvenirs of type A and 20 souvenirs of
type B is manufactured.
27. In answering a question on a multiple choice questions test with four choices in each question, out of which only one is correct, a student either guesses or copies or knows the answer. The probability that he makes a guess is 1/4 and the probability that he copies is also 1/4 . The probability that the answer is correct, given that he copied it is 3/4 . Find the probability that he knows the answer to the question, given that he correctly answered it.
Sol. Let E1 : student guesses the answer, E2 : student copies the answer, E3 : student knows the
answer and A : student answers the question correctly.
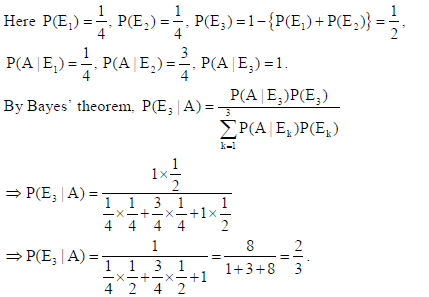
28. An isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a. Show that the area of the triangle is maximum when θ = π/6
Sol. Consider the figure shown.

29. Using elementary row transformations, find the inverse of the matrix
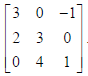
Sol.


OR
Using matrices, solve the following system of linear equations :
2x + 3y +10z = 4,
4x − 6y + 5z =1,
6x + 9y − 20z = 2 .
Sol.