Case Study Chapter 2 Polynomials Mathematics

Refer to Case Study Chapter 2 Polynomials Mathematics, these class 10 maths case study based questions have been designed as per the latest examination guidelines issued for the current academic year by CBSE, NCERT, KVS. Students should go through these solves case studies so that they are able to understand the pattern of questions expected in exams and get good marks.

Chapter 2 Polynomials Mathematics Case Study Based Questions

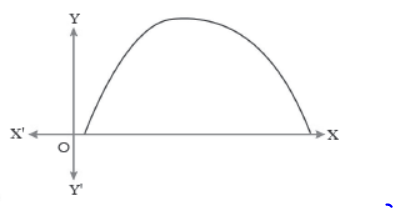
I. The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.

Question. If a and 1/α are the zeroes of the quadratic polynomial 2x² – x + 8k, then k is     
(a) 4
(b) 1 4
(c) –1/ 4
(d) 2

Question. If the sum of the roots is –p and product of the roots is – 1 , p then the quadratic polynomial is   
(a) k( − px² + x/ p +1)
(b) k (px² – x/p –1)
(c) k (x² + px – 1/ p)
(d) k (x² – px + 1 / p)

Question. In the standard form of quadratic polynomial, ax² + bx + c, a, b and c are    
(a) All are real numbers.
(b) All are rational numbers.
(c) ‘a’ is a non zero real number and b and c are any real numbers.
(d) All are integers.

Question. If the roots of the quadratic polynomial are equal, where the discriminant D = b² – 4ac, then   
(a) D > 0
(b) D < 0
(c) D ≥ 0
(d) D = 0

Question. The graph of x² + 1 = 0     
(a) Intersects x-axis at two distinct points.
(b) Touches x-axis at a point.
(c) Neither touches nor intersects x-axis.
(d) Either touches or intersects x-axis.

II. An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.

Question. In the graph, how many zeroes are there for the polynomial ? 

(a) 0
(b) 1
(c) 2
(d) 3

Question. The two zeroes in the above shown graph are   
(a) 2, 4
(b) –2, 4
(c) –8, 4
(d) 2, –8

Question. The zeroes of the quadratic polynomial 4 √3x² + 5x – 2√3 are   
(a) 2/√3 , √3/ 4
(b) – 2/√3 , √3/ 4
(c) 2/√3 , – √3/ 4
(d) – 2/√3 , − √3/ 4

Question. The shape of the poses shown is   
(a) Spiral
(b) Ellipse
(c) Linear
(d) Parabola

Question. The graph of parabola opens downwards, if__________.   
(a) a ≥ 0
(b) a = 0
(c) a < 0
(d) a > 0

III. Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.

Question. The graph of parabola opens upwards, if____________.   
(a) a = 0
(b) a < 0
(c) a > 0
(d) a ≥ 0

Question. What will be the expression of the polynomial ?   
(a) x³ + 2x² − 5x − 6
(b) x³ + 2x² − 5x + 6
(c) x³ + 2x² + 5x − 6
(d) x³ + 2x² + 5x + 6

Question. Observe the following graph and answer   

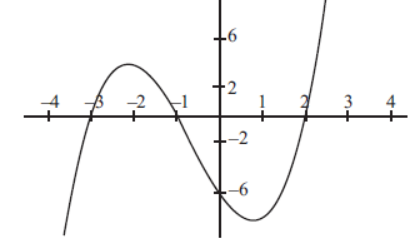
In the above graph, how many zeroes are there for the polynomial ?
(a) 0
(b) 1
(c) 2
(d) 3

Question. The three zeroes in the above shown graph are   
(a) 2, 3, –1
(b) –2, 3, 1
(c) –3, –1, 2
(d) –2, –3, –1

Question. The shape of the path traced shown is   
(a) Spiral
(b) Ellipse
(c) Linear
(d) Parabola

l. Read the following and answer The wall of room is decorated with beautiful garlands, each garland forming a parabola. 

Question. A quadratic polynomial with the sum and product of its zeroes as –1 and –2 is   
(a) x²+ x – 2
(b) x² –x – 2
(c) x²+ 2x – 1
(d) x² –2x – 1

Question. The number of zeros of a quadratic polynomial is   
(a) equal to 2
(b) equal to 1
(c) more than 2
(d) atmost 2

Question. If a, b are the zeros of the polynomial f (x)=x² – 7x+12 then the value of 1/α + 1/β is   
(a) –7
(b) 12
(c) 7/12 
(d) –7/12 

Question. If one of the zeroes of the quadratic polynomial (k–2) x² –2x –5 is –1, then the value of k is     
(a) 3
(b) 5
(c) –5
(d) –3

Question. What type of polynomial does a parabola represent ?   
(a) linear
(b) quadratic
(c) cubic
(d) None of these

ll. Read the following and answer Water flowing in a fountain follows trajectory as shown below:   

Question. If the trajectory is represented by x² –3x – 18 , then its zeros are     
(a) (6, – 3)
(b) (–6, 3)
(c) (3, – 3)
(d) (–6, –3)

Question. If a and b are the roots of the equation 2×2 –3x – 5 then a+b is equal to   
(a) 3
(b) –3
(c) –3/2
(d) 3/2

Question. If –1/3 is one of the zeroes of 9x² – kx – 5, then the value of k is   
(a) 9
(b) 3
(c) 12
(d) 4

Question. The shape formed by the water trajectory is   
(a) ellipse
(b) oval
(c) parabola
(d) spiral

Question. Number of zeroes of polynomial is equal to the number of points where the graph of polynomial   
(a) intersects x- axis
(b) intersects y- axis
(c) intersects y- axis or x- axis
(d) none of the above

lll. Read the following and answer The path moved by a group of ants has been traced on a floor which is shown below:   

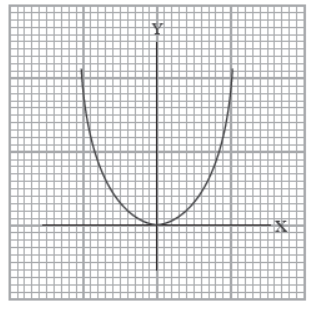
Question. The number of zeroes of the polynomial represented by the path is   
(a) one
(b) at most two
(c) atleast two
(d) less than two

Question. If the sum and product of zeroes of the polynomial representing the path are 6 and –16, then the polynomial is   
(a) x² –10x+96
(b) x² –6x+16
(c) x² –6x – 16
(d) x²+6x

Question. If the path is represented by x²+2x –3, then its zeroes are   
(a) (–3, 1)
(b) (3, –1)
(c) (2, –3)
(d) (–2, 3)

Question. The number of zeroes of the polynomial f (x)=x² –8 are   
(a) 0
(b) 1
(c) 2
(d) 3

Question. The shape formed by the path is     
(a) ellipse
(b) oval
(c) parabola
(d) spiral

lV. Read the following and answer A runner is running along a straight path parallel to a given boundary. 

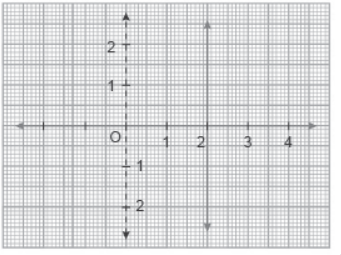
Question. How many zeros does it have?     
(a) 0
(b) 1
(c) 2
(d) more than 1

Question. If one zero of the polynomial p(z)=3z²–10z+m is reciprocal of other, then value of m is     
(a) 2
(b) 3
(c) 5
(d) 6

Question. The equation of this graph can be written as   
(a) x = 2
(b) y = 2
(c) x = 0
(d) y = 0

Question. If the graph would have been parallel to x-axis, then its number of zeroes would be     
(a) 0
(b) 1
(c) 2
(d) more than 1

Question. The path of the runner represents the graph of a   
(a) cubic polynomial 
(b) quadratic polynomial
(c) linear polynomial
(d) None of these

V. Read the following and answer A child was flying a kite, and its string got struck into a tree and touched ground as shown in figure.

Question. If one zero of the polynomial x² – 12x+(3k – 1) is five times the other, then the value of k is   
(a) 2
(b) 3
(c) 10
(d) 7

Question. Which of the following could be the equation of the given graph?   
(a) (x + 1)² = (x – 3)² + 5
(b) x+9=3 – 2x
(c) 1+x³=2
(d) 2x²+3x – 6=0

Question. The string of the kite represents the graph of a     
(a) linear polynomial
(b) quadratic polynomial
(c) cubic polynomial
(d) polynomial of degree more than

Question. The number of zeros of a cubic polynomial is     
(a) 2
(b) atmost 2
(c) 3
(d) atmost 3

Question. The zeros of the polynomial 6x²– 3 –7x are     
(a) 6, –7
(b) 3, –7
(c) 3/2 , –1/3 
(d) 3/2 , 1/3

Vl. Read the following and answer A few children are playing with a skipping rope. When two of them hold it in their hands, as shown in the figure, it formed a mathematical shape. 

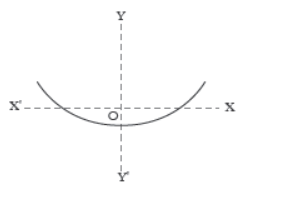
Question. If the polynomial x² + kx – 15 represents such a curve, with one of its zeros as 3, then the value of k is     
(a) 3
(b) 5
(c) 2
(d) –2

Question. If the graph of a polynomial intersects the x-axis at only one point, then it     
(a) is always a linear polynomial
(b) can be a quadratic polynomial
(c) can never be a quadratic polynomial
(d) can neither be linear nor quadratic polynomial

Question. If both the zeros of a quadratic polynomial ax²+bx+c are equal and opposite in sign, then value of b is     
(a) 1
(b) –1
(c) 2
(d) 0

Question. The name of the shape formed is   
(a) parabola
(b) ellipse
(c) oval
(d) spiral

Question. If the graph of a polynomial has such a shape, it is always     
(a) linear
(b) quadratic
(c) cubic
(d) None of these