Case Study Chapter 6 Triangles Mathematics

Refer to Case Study Chapter 6 Triangles Mathematics, these class 10 maths case study based questions have been designed as per the latest examination guidelines issued for the current academic year by CBSE, NCERT, KVS. Students should go through these solves case studies so that they are able to understand the pattern of questions expected in exams and get good marks.

Chapter 6 Triangles Mathematics Case Study Based Questions

I. Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles.The height of Vijay’s house if 20m when Vijay’s house casts a shadow 10m long on the ground. At the same time, the tower casts a shadow 50m long on the ground and the house of Ajay casts 20m shadow on the ground.

Question. What is the height of Ajay’s house?   
(a) 30m   
(b) 40m
(c) 50m
(d) 20m

Question. When the tower casts a shadow of 40m, same time what will be the length of the shadow of Vijay’s house?   
(a) 15m
(b) 32m
(c) 16m
(d) 8m

Question. What is the height of the tower?   
(a) 20m
(b) 50m
(c) 100m
(d) 200m

Question. When the tower casts a shadow of 40m, same time what will be the length of the shadow of Ajay’s house?   
(a) 16m
(b) 32m
(c) 20m
(d) 8m

Question. What will be the length of the shadow of the tower when Vijay’s house casts a shadow of 12m?   
(a) 75m
(b) 50m
(c) 45m
(d) 60m

l. Read the following and answer Two trees are standing parallel to each other. The bigger tree 8 m high, casts a shadow of 6 m. 

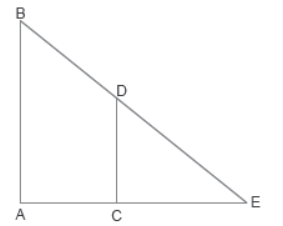
Question. If the ratio of the height of two trees is 3 : 1, then the shadow of the smaller tree is     
(a) 2 m
(b) 6 m
(c) 8/3 m
(d) 8 m

Question. If , ΔABC ∼ ΔPQR , ar (ΔABC)/ ar (ΔPQR) = 4/25 , PQ = 10 cm, then AB is equal to     
(a) 4 cm
(b) 2 cm
(c) 5 cm
(d) 5 8 cm

Question. If AB and CD are the two trees and AE is the shadow of the longer tree, then   
(a) ΔAEB ∼ ΔCED
(b) ΔABE ∼ ΔCED
(c) ΔAEB ∼ ΔDEC
(d) ΔBEA ∼ ΔDEC

Question. Since AB ll CD , so by basic proportionality theorem, we have   
(a) AE/CE = BD/DE 
(b) AC/AE = DE/BE
(c) AE/CE = AB/CD
(d) AE/CE = BE/DE

Question. The distance of point B from E is   
(a) 10 m
(b) 8 m
(c) 18 m
(d) 10/3 m

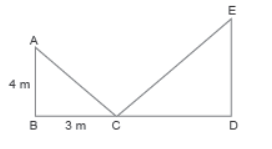
ll. Read the following and answer A ladder was placed against a wall such that it touches a point 4 m above the ground. The distance of the foot of the ladder from the bottom of the ground was 3 m. Keeping its foot at the same point, Akshay turns the ladder to the opposite side so that it reached the window of his house.   

Question. In an isosceles right triangle PQR, right angled at P, then     
(a) QR ² = 2PQ ²
(b) QP ² = 2PR ²
(c) QP ² = 2QR ²
(d) PR ² = 2QR ²

Question. If OA² =  OB² + AB², then     
(a) ΔOBA is an equilateral triangle.
(b) ΔOAB is an isosceles right triangle.
(c) ΔOAB is a right triangle right angled at O.
(d) ΔOAB is a right triangle right angled at B.

Question. The theorem which can be used for find the length of the ladder is   
(a) Thales Theorem
(b) Converse of Thales Theorem
(c) Pythagoras Theorem
(d) Converse of Pythagoras Theorem

Question. The length of the ladder, in metre is   
(a) 4 m
(b) 5 m
(c) 9 m
(d) 2 m

Question. If the window of the house is 3 m above the ground, then the distance of the point C from D is   
(a) 3 m
(b) 4 m
(c) 5 m
(d) 3.5 m

lll. Read the following and answer Two buildings (say A and B) are located 12 m apart. The height of the two buildings are 32 m and 41 m.

Question. The distance DF is equal to     
(a) 15 m
(b) 12 m
(c) 9 m
(d) 21 m

Question. In a triangle PQR, PQ = 7 cm, QR = 25 cm, RP = 24 cm, then the triangle is right angled at     
(a) P
(b) Q
(c) R
(d) can’t say

Question. ABC is an equilateral triangle of side ‘2a’ units. The length of each of its altitude is       
(a) a units
(b) 2a units
(c) √2 a units
(d) √3 a units

Question. The distance between the top of the two buildings can be calculated using     
(a) Thales Theorem
(b) Pythagoras Theorem
(c) Converse of Thales Theorem
(d) Converse of Pythagoras Theorem

Question. The length EF in the figure is     
(a) 32 m 
(b) 41 m
(c) 41 m/2
(d) 9 m

lV. Read the following and answer A farmer had a triangular piece of land. He put a fence, parallel to one of the sides of the field as shown in the figure.   

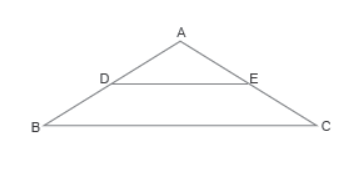
Question. If AD = x + 1, DB = 3x – 1, AE = x + 3, EC = 3x + 4, then     
(a) x = 5
(b) x = 7
(c) x = 8
(d) x = 4

Question. If the point D is 20 m away from A, where as AB and AC are 80 m and 100 m respectively, then     
(a) AE = 20 m
(b) EC = 25 cm
(c) AE = 25 cm
(d) EC = 60 cm

Question. Which of the following is not true?     
(a) AD/AB = AE/AC 
(b) AD/AE = AB/AC 
(c) AB/BD = AC/EC
(d) BD/AD = AE/EC 

Question. Which of the following statements is true?     
(a) AD/DB =  AE/EC , using Thales Theorem
(b) AD/DB =  AE/EC  , using Pythagoras Theorem
(c) AD/DB =  AE/EC , using Pythagoras Theorem
(d) AD/DB =  AE/EC , using Thales Theorem

Question. If P and Q are the mid points of sides YZ and XZ respectively, then     
(a) PQ ll XY
(b) PQ ll YZ
(c) PQ ll ZX
(d) None of these

V. Read the following and answer The ratio of two corresponding sides in similar figures is called scale factor. Scale factor = Length of image / Actual length of object   

Question. Two similar triangles have a scale factor of 1 : 2. Then their corresponding altitudes have a ratio       
(a) 2 : 1
(b) 4 : 1
(c) 1 : 2
(d) 1 : 1

Question. If two similar triangles have a scale factor of 2 : 5, then which of the following statements is true ?     
(a) The ratio of their medians is 2 : 5.
(b) The ratio of their altitudes is 5 : 2.
(c) The ratio of their perimeters is 2 × 3 : 5.
(d) The ratio of their altitudes is 22 : 52.

Question. The shadow of a statue 8 m long has length 5 m. At the same time the shadow of a pole 5.6 m high is     
(a) 3 m
(b) 3.5 m
(c) 4 cm
(d) 4.5 m

Question. For two similar polygons which of the following is not true?     
(a) They are not flipped horizontally.
(b) They are dilated by a scale factor.
(c) They cannot be translated down.
(d) They are mirror images of each other.

Question. A model of a car is made on the scale 1 : 8. The model is 40 cm long and 20 cm wide. The actual length of car is     
(a) 320 cm
(b) 160 cm
(c) 5 cm
(d) 2.5 cm