Case Study Chapter 3 Linear Equations Mathematics

Refer to Case Study Chapter 3 Linear Equations Mathematics, these class 10 maths case study based questions have been designed as per the latest examination guidelines issued for the current academic year by CBSE, NCERT, KVS. Students should go through these solves case studies so that they are able to understand the pattern of questions expected in exams and get good marks.

Chapter 3 Linear Equations Mathematics Case Study Based Questions

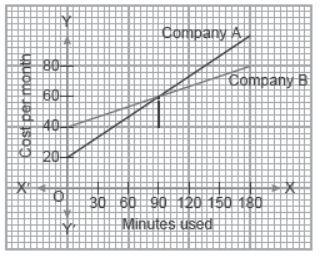
l. Read the following and answer A man is trying to choose between two phone plans. The first plan of company A, cost ` 20 per month, with calls costing an additional 25 paise per minute. The second plan of company B charges ` 40 per month, but calls cost 8 paise per minute. These two situations are shown below which represent linear equations. The total cost for the two company’s are given by   
y = 0.25x + 20
and y = 0.08x + 40
where x is the minutes used and y is the total cost per month.

Question. Given system of linear equations x + 2y – 4 = 0, 2x + 4y – 12 = 0 represents     
(a) parallel lines
(b) intersecting lines
(c) coincident lines
(d) can’t say

Question. Solution of system of linear equations x + 2y = – 1 and 2x – 3y = 12 is    
(a) (–3, 2)
(b) (–3, –2)
(c) (3, – 2)
(d) (3, 2)

Question. If the system of pair of linear equations kx + 2y = 5, 3x + y = 1 has a unique solution, then   
(a) k 2 3 !
(b) k = 6
(c) k ≠ 6
(d) k 3 2

Question. If a person takes first plan and calls for 90 minutes in a month then how much amount he will have to pay whose cost for a month is given by y = 0.25x + 20?   
(a) ₹ 20
(b) ₹ 40
(c) ₹ 42.50
(d) ₹ 45

Question. Another person takes second plan and also calls for 90 minutes in a month, then the amount which he has to pay when total cost is given by y = 0.08x + 40, is   
(a) ₹ 45
(b) ₹ 47
(c) ₹ 45.20
(d) ₹ 47.20

ll. Read the following and answer A cricket bat manufacturer’s revenue is the function used to calculate the amount of money that comes into the business. It can be represented by the equation R = xp, where x = quantity and p = price.
The revenue function is shown in orange colour in the figure. The cost function is the function used to calculate the costs of doing business. It includes fixed costs, such as rent and salaries, and variable costs such as utilities. The cost function is shown in blue colour in figure.

The x-axis represents quantity (in hundreds) of units, and the y-axis represents either cost or revenue (in thousand of rupees).
The profit function is the difference of revenue function and the cost function, written as
P(x) = R(x) – C(x)
Now, let C(x) = 100x + 30000 and R(x) = 150x
If we replace function by y, we get
Linear equations are y = 100x + 30000 and y = 150x

Question. The number of bat manufactured (x) so that there is no profit or loss for the manufacturer is     
(a) x = 200
(b) x = 300
(c) x = 400
(d) x = 600

Question. Solution of the system of linear equations x + y = 1, 2x – 3y = 7, is       
(a) (1, 2)
(b) (2, 1)
(c) (2, –1)
(d) (–2, –1)

Question. The value of k for which the system of linear equations 4x + 5y = 3 and kx + 15y = 9 has infinitely many solutions is     
(a) k = 3
(b) k = 4
(c) k = 12
(d) k = 8

Question. If the cost and revenue are given by the linear equations y = 0.85x + 35000 and y = 1.55x respectively, and the break-even point is the point at which the two lines intersect, then its break even point is       
(a) (50000, 77500)
(b) (50000, 60000)
(c) (45000, 50000)
(d) (45000, 60000)

Question. The system of linear equations 3x + 2y = 12, 5x – 2y = 4 represents       
(a) parallel lines
(b) intersecting lines
(c) coincident lines
(d) can’t say

lll. Read the following and answer The scissors which is so common in our daily life use, its blades represent the graph of linear equations.

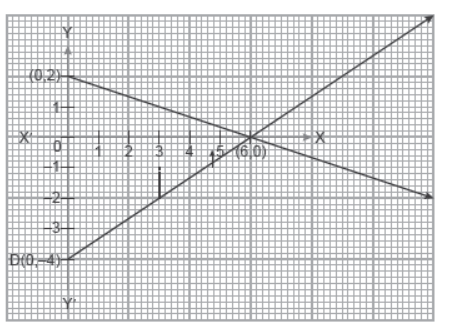
Let the blades of a scissor are represented by the system of linear equations:
     x + 3y = 6 and 2x – 3y = 12

Question. If a pair of linear equations in two variables is consistent, then the lines represented by two equations are 
(a) intersecting
(b) parallel
(c) always coincident
(d) intersecting or coincident

Question. The number of solution of the system of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 is     
(a) 0
(b) 1
(c) 2
(d) infinitely many

Question. If (1, 2) is the solution of linear equations ax + y = 3 and 2x + by = 12, then values of a and b are respectively     
(a) 1, 5
(b) 2, 3
(c) –1, 5
(d) 3, 5

Question. The pivot point (point of intersection) of the blades represented by the linear equation x + 3y = 6 and 2x – 3y = 12 of the scissor is       
(a) (2, 3)
(b) (6, 0)
(c) (3, 2)
(d) (2, 6)

Question. The points at which linear equations x + 3y = 6 and 2x – 3y = 12 intersect y – axis respectively are     
(a) (0, 2) and (0, 6)
(b) (0, 2) and (6, 0)
(c) (0, 2) and (0, –4)
(d) (2, 0) and (0, –4)

lV. Read the following and answer A pen stand with a pen is represented by the system of linear equations y = 0 and 3x + 2y = 6.

Question. The value of k for which the system of equations kx – 5y = 2 and 6x + 2y = 7 has no solution, is       
(a) 30
(b) –30
(c) 15
(d) –15

Question. The linear equation 3x + 2y = 6 intersects the y–axis at the point       
(a) (0, 3)
(b) (0, 2)
(c) (0, –3)
(d) (2, 3)

Question. The system of linear equations y = 0 and 3x + 2y = 6 represents the pen stand and a pen respectively then their point of contact (intersection) is   
(a) (0, 3)
(b) (2, 0)
(c) (3, 2)
(d) (3, 0)

Question. The pair of linear equation y = x and x + y = 6 intersect each other at point   
(a) (4, 2)
(b) (4, 4)
(c) (3, 3)
(d) (3, 2)

Question. The system of linear equations 3x + 6y = 3900 and x + 3y = 1300 represent the lines which are       
(a) parallel
(b) intersecting
(c) coincident
(d) can’t say

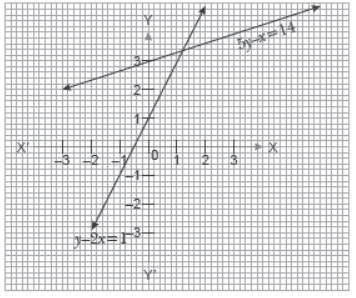
V. Read the following and answer A boy enjoying the pizza with his friends and share with them by slicing it. During slicing the pizza, he noticed that the pair of linear equations formed.
Let these pair of linear equations be y – 2x = 1 and 5y – x = 14.   

Question. The system of linear equations 2x – 3y + 6 = 0 and 2x + 3y – 18 = 0       
(a) has a unique solution
(b) has no solution
(c) has infinitely many solution
(d) may or may not have a solution

Question. If a pair of linear equations in two variables is inconsistent, then the lines represented by two equations are         
(a) intersecting
(b) parallel
(c) always coincident
(d) Intersecting or coincident

Question. The point of intersection of the lines given by the equations y – 2x = 1 and 5y – x = 14 is           
(a) (–2, 3)
(b) (–4, 2)
(c) (6, 4)
(d) (1, 3)

Question. The value(s) of k for which the system of linear equations 2x – ky + 3 = 0 and 3x + 2y – 1 = 0 has no solution, is         
(a) 4/3
(b) –4/3
(c) 6
(d) –6

Question. The linear equation y – 2x = 1 intersect the y–axis at point       
(a) (−1/2 , 0)
(b) (0, 1)
(c) (0, –14)
(d) (0 , 14/5)