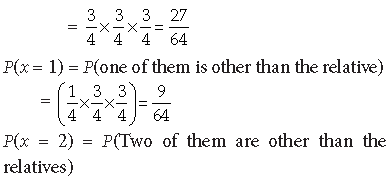Please refer to Class 12 Mathematics Sample Paper Set C with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
Section – A
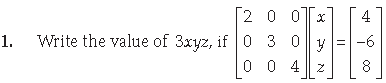
Answer.
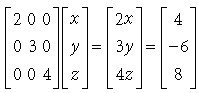
⇒ 2x = 4, 3y = –6, 4z = 8
⇒ x = 2, y = –2, z = 2
⇒ 3xyz = 3 × 2 × (–2) × 2 = –24
2. If A is square matrix of order 3 × 3 such that |adj A|= 324 then find |A|.
Answer.
If A be a non-singular square matrix of order n × n, then |adj A| = |A|n – 1
|adj A| = 324 = |A|n–1 = |A|2 = 324 ⇒ |A| = 18
Answer.
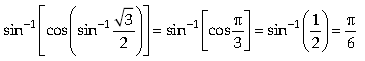
4. The total revenue received from the sale of x units of a product is given by R(x) = 15x2 + 4x + 30. Find the marginal revenue when x = 5, where by marginal revenue we mean the rate of R(x) with respect to the number of items sold at an instant.
Answer.
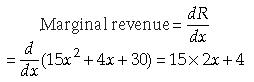
when x = 5, we have
Marginal Revenue = 15 × 10 + 4 = 150 + 4 = 154
Hence, the required marginal revenue is ` 154.
5. For what values of x will the given matrix
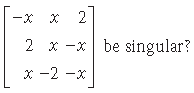
Answer. Given matrix is singular if its determinant. is zero
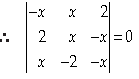
⇒ = – x(–x2 – 2x) – x(– 2x + x2) + 2(– 4 – x2) = 0
⇒ x3 + 2x2 + 2x2 – x3 – 8 – 2x2 = 0
⇒ 2x2 – 8 = 0 ⇒ x = ± 2
6. The probability that a person will get an electric contract is 2/5 and the probability that he will not get plumbing contract is 4/7. If the probability of getting at least one contract is 2/3, what is the probability that he will get both?
Answer. Consider the following events :
A = Person gets an electric contract,
B = Person gets plumbing contract
We have,
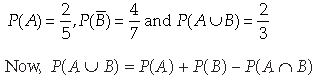
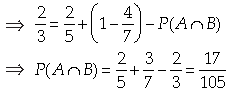
7. Write the inverse of the matrix
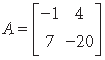
using elementary row transformation.
Answer. We have A = IA
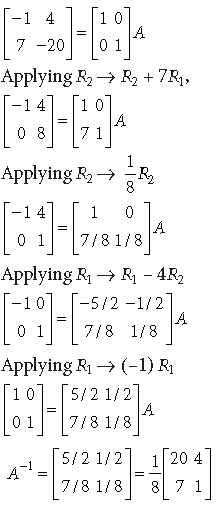
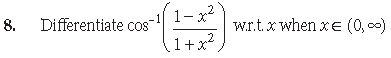
Answer.
9. If the area above x-axis, bounded by the curves
Answer. It is given that
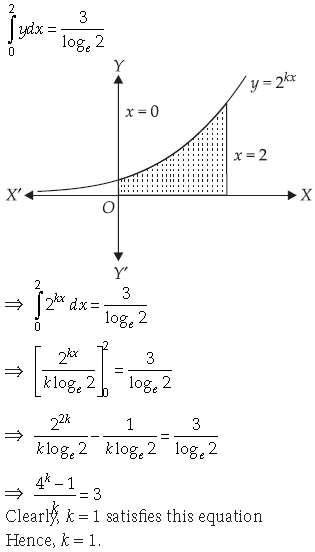
10. Find the solutions of the equation
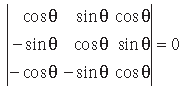
Answer. Applying R1 → R1 + R3, we get
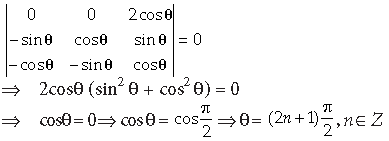
11. A four digit number is formed using the digits 1, 2, 3, 5 with no repetitions. Write the probability that the number is divisible by 5.
Answer. A four digit number formed using the digits 1, 2, 3 and 5 without repetitions will be divisible by 5 if and only if the unit’s digit is 5.
So, the number of ways to fill the rest three places is 3!.
Further the total number of number that can be formed = 4!
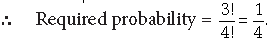
12. Obtain the general solution of the differential
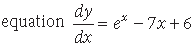
Answer.
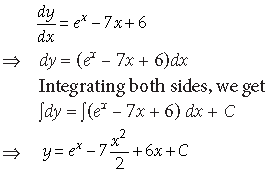
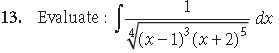
Answer.
Section – C
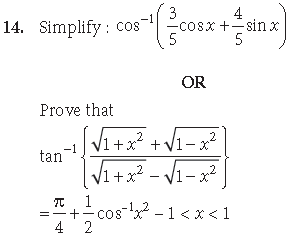
Answer.

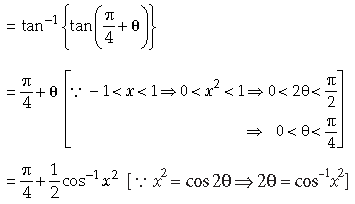
15. Three shopkeepers A, B, C are using polythene, handmade bag and newspaper envelopes as carry bags. It is found that the shopkeepers A, B, C are using (20, 30, 40), (30, 40, 20), (40, 20, 30) polythene, handmade bags and newspapers envelopes, respectively. The shopkeepers A, B, C spend ₹ 250, ₹ 270 and ₹ 200 on these carry bags respectively.
(i) Represent the above situation by a matrix equation and form linear equations using matrix multiplication.
(ii) Is it possible to find the cost of each carry bag using matrices.
Answer. (i) Let x, y, z be the cost of polythene, handmade bags and newspaper envelopes respectively used by shopkeepers A, B and C.
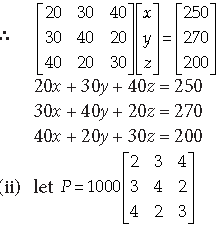
⇒ |P| = 1000[2(12 – 4) – 3(9 – 8) + 4(6 – 16)]
⇒ |P| = 1000[16 – 3 – 40] = 1000 [–27] = –27000
∵ A–1 exists, so equations have a unique
solution.
∴ We can find the cost of carry bag using matrices.
Answer.
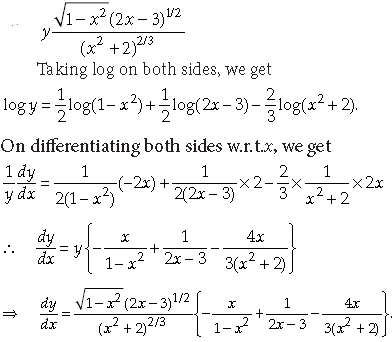
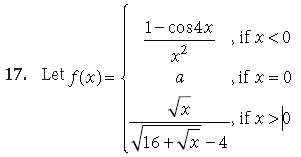
Determine the value of a so that f(x) is continuous at x = 0.
Answer. For f(x) to be continuous at x = 0, we must have
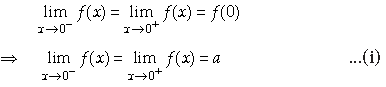

18. Evaluate
Answer.
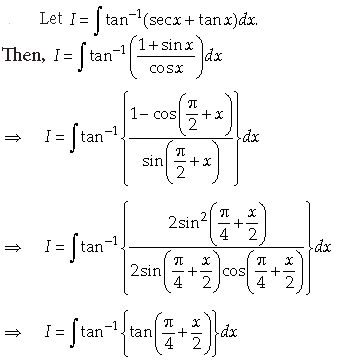
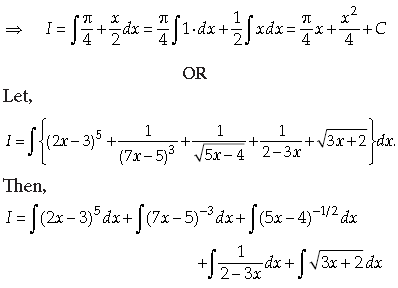
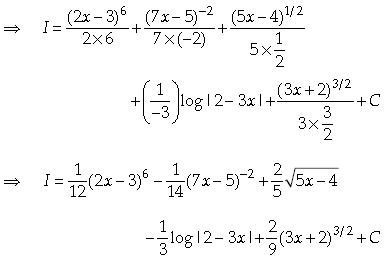
19. Let S and T be two sets. Show that f : S × T → T × S defined as f(s, t) = (t, s) is one-one and onto.
Answer.
One-One : Let (s1, t1) and (s2, t2) ∈ S × T such
that
f(s1, t1) = f(s2, t2)
⇒ (t1, s1) = (t2, s2) ⇒ t1 = t2 and s1 = s2
⇒ (s1, t1) = (s2, t2)
Thus, f(s1, t1) = f(s2, t2) ⇒ (s1, t1) = (s2, t2) for all
(s1, t1), (s2, t2) ∈ S × T.
So, f is one-one
Onto : Let (t, s) be an arbitrary element of T × S.
Then, t ∈ T and s ∈ S
⇒ (s, t) ∈ S × T.
Thus, for all (t, s) ∈ T × S there exists (s, t) ∈ S × T
such that f (s, t) = (t, s)
So, f : S × T → T × S is an onto function.
Hence, f is one-one and onto.
20. Solve the differential equation:
(1 + y2) (1 + logx) dx + x dy = 0.
Answer. (1 +y2) (1 + logx) dx + x dy = 0
⇒ (1 + y2)(1 + logx)dx = –xdy
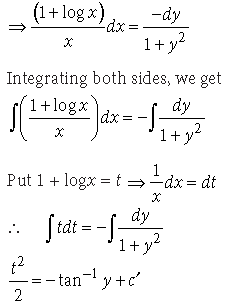
⇒ (1 + logx)2 = –2tan–1y + 2c′
⇒ 2tan–1y = –(1 + logx)2 + 2c′
⇒ 2tan–1y = C – (1 + logx)2
21. If a̅ and b are non-collinear vectors and vectors a̅ = (x + 4y) a̅ + (2x + y + 1) b̅ and B̅, = (–2x + y + 2) a̅ + (2x –3y – 1) b̅ are connected by the relation 3a̅ = 2B̅,, find x and y.
Answer. We have, 3a̅, 2B̅
⇒ 3{(x + 4y)a̅, + (2x + y + 1)b̅}
= 2{(−2x + y + 2)a̅, + (2x − 3y − 1)b̅}
⇒ (3x + 12y + 4x − 2y − 4)a̅,
+(6x + 3y + 3 − 4x + 6y + 2)b̅ = 0¯
⇒ 7x + 10y – 4 = 0 and 2x + 9y + 5 = 0
⇒ x = 2, y = –1.
22. Show that the lines
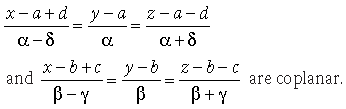
OR
Find the length and the foot of the perpendicular from the point (7, 14, 5) to the plane 2x + 4y – z = 2.
Answer. We know that the lines

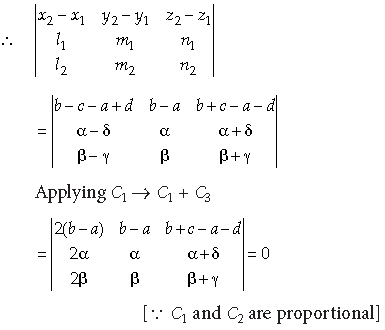
Hence, given lines are coplanar.
OR
Let M be the foot of the perpendicular from P on the plane 2x + 4y – z = 2. Then, PM is normal to the plane. So, its direction ratios are 2, 4, –1.
Since PM passes through P(7, 14, 5). Therefore, its equation is
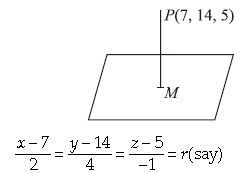
Let the coordinates of M be (2r + 7, 4r + 14, –r + 5).
Since M lies on the plane 2x + 4y – z = 2. Therefore,
2(2r + 7) + 4 (4r + 14) – (–r + 5) = 2
⇒ 21r + 63 = 0 ⇒ r = –3
So, the coordinates of M are (1, 2, 8)
Now,
PM = Length of the perpendicular from P
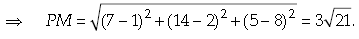
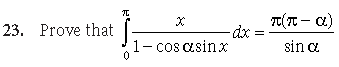
Answer.

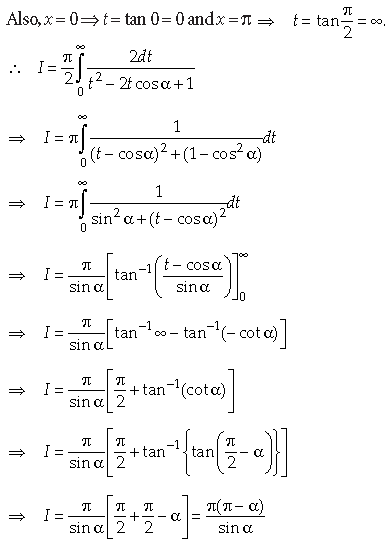
Section – D
24. Find the points on the curve 9y2 = x3 where normal to the curve makes equal intercepts with the axes.
OR
Show that the triangle of maximum area that can be inscribed in a given circle is an equilateral triangle.
Answer. Let the required point be (x1, y1).
Equation of the curve is 9y2 = x3.
Since (x1, y1) lies on the curve. Therefore,
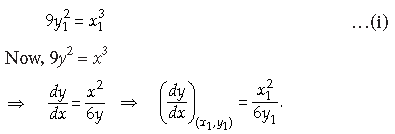
Since the normal to the curve at (x1, y1) make equal intercepts with the coordinate axes. Therefore, slope of the normal = ±1
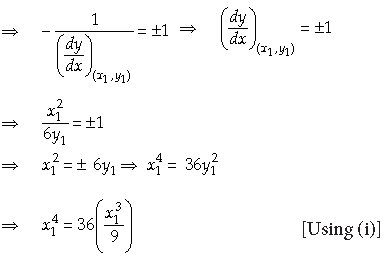
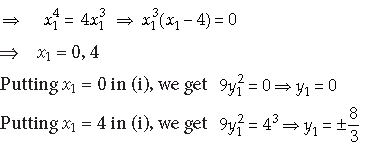
But, the line making equal intercepts with the coordinate axes cannot pass through the origin.
Hence, the required points are (4, 8/3) and (4, –8/3).
OR
Let ABC be a triangle inscribed in a given circle with centre O and radius r. The area of the triangle will be maximum if its vertex A opposite to the base BC is at a maximum distance from the base BC. This is possible only when A lies on the diameter perpendicular to BC. Thus, AD ^ BC. So, triangle ABC must be an isosceles triangle.
Let OD = x.
In right triangle ODB, we have

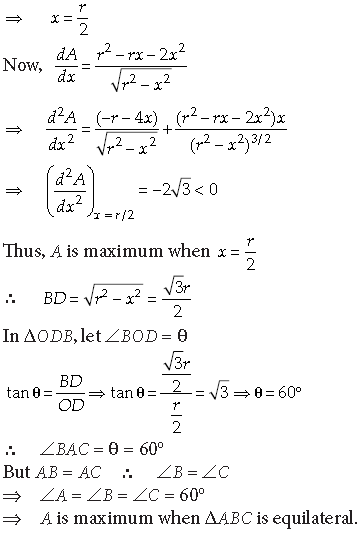
25. Find the area of the region
{(x, y) : x2 + y2 ≤ 1 ≤ x + y}.
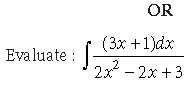
Answer. Let R = {(x, y) : x2 + y2 ≤ 1 ≤ x + y}. Then
⇒ R = R1 ∩ R2, where
R1 = {(x, y) : x2 + y2 ≤ 1} and R2 = {(x, y) : 1 ≤ x +y}
R1 : Clearly x2 + y2 = 1 represents a circle with centre at (0, 0) and radius 1.
Since x2 + y2 ≤ 1, so region R1 represents the
interior of circle x2 + y2 = 1.
R2 : Since x + y = 1 is the equation of a straight line cutting x and y-axes at (1, 0) and (0, 1)
respectively. This line divides the xy-plane in two parts represented by x + y ≤ 1 and x + y ≥ 1. Since (0, 0) does not satisfy the inequality x + y ≥ 1. So,
R2 is the region lying above the line x + y = 1.
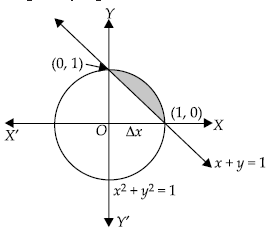
Hence, region R is the shaded region shown in figure.
So, required area is given by
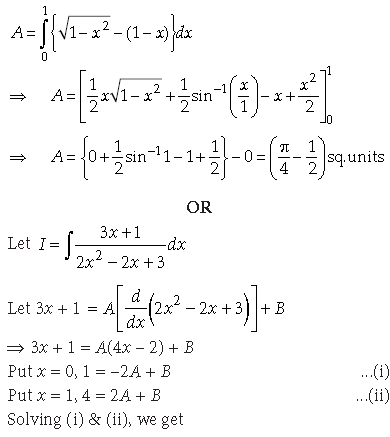
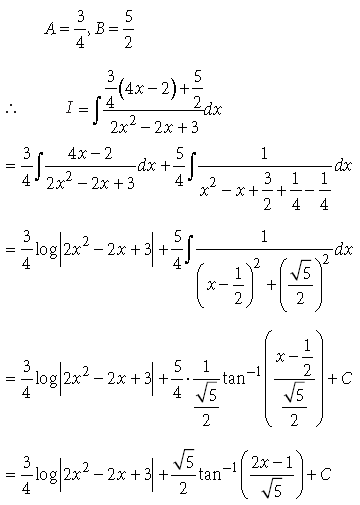
26. Solve the following initial value problem.
(xey/x + y)dx = xdy, y(1) = 1
Answer. (xey/x + y)dx = xdy
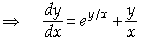
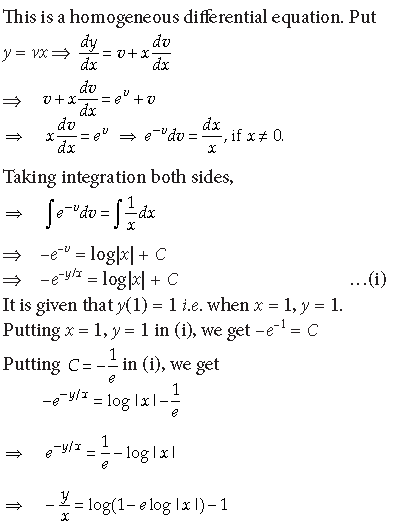
⇒ y = x – xlog(1 – elog|x|)
Hence, y = x – xlog(1 – elog|x|), is the solution of
the given equation.
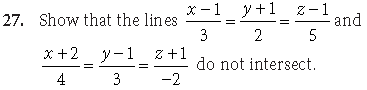
Answer. We have,
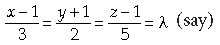
⇒ x = 3λ + 1, y = 2λ – 1, z = 5λ + 1.
So, the coordinates of a general point on this line are (3λ + 1, 2λ – 1, 5λ + 1).
The equation of the second line is
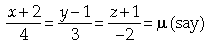
⇒ x = 4μ – 2, y = 3μ + 1, z = –2μ – 1
So, the coordinates of a general point on this line are (4μ – 2, 3μ + 1, –2μ – 1).
If the line intersect, then they have a common point. So, for some values of l and m, we must have
3λ + 1 = 4μ – 2, 2λ – 1 = 3μ + 1 and 5λ + 1 = –2μ –1.
⇒ 3λ – 4μ = –3 …(i)
2λ – 3μ = 2 …(ii)
and 5λ + 2μ = –2 …(iii)
Solving (i) and (ii), we obtain λ = –17 and μ = –12.
These values of l and m do not satisfy the third equation.
Hence, the given lines do not intersect.
28. A village has 500 hectares of land to grow two types of plants, X and Y. The contribution of total amount of oxygen produced by plant X and plant Y are 60% and 40% per hectare respectively. To control weeds, a liquid herbicide has to be used for X and Y at rates of 20 litres and 10 litres per hectare, respectively. Further no more than 8000 litres of herbicides should be used in order to protect aquatic animals in a pond which collects drainage from this land. How much land should be allocated to each crop so as to maximise the total production of oxygen?
(i) How do you think excess use of herbicides affect our environment?
(ii) What are the general implications of this question towards planting trees around us?
Answer. Let plants X and Y be grown in x and y hectares.
So, x ≥ 0 and y ≥ 0
x + y ≤ 500 …(i)
Contribution of oxygen by the plants
= 60% of x + 40% of y
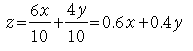
Also, Amount of liquid herbicides required
= (20x + 10y) litres
Given 20x + 10y ≤ 8000
⇒ 2x + y ≤ 800 …(ii)
The L.P.P for given problem is
Maximize, Z = 0.6x + 0.4y
such that x + y ≤ 500 …(iii)
and 2x + y ≤ 800 …(iv)
x, y ≥ 0
Sketching a graph for the above L.P.P, we get the region shown in the figure.
Solving x + y = 500 and 2x + y = 800, we get
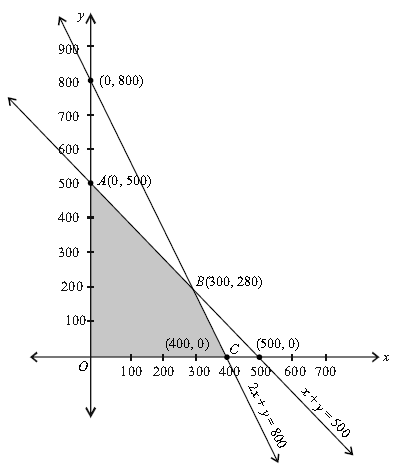

Maximum production of oxygen will be achieved when plant X is planted in 300 hectares and plant Y is planted in 200 hectares.
(i) Excess herbicide will we get absorbed in the soil and may contaminate the water source also. Thus it can affect the whole ecosystem.
(ii) Care should be taken while planting trees that the variety of the plants is such that they provide more oxygen for our environment
29. There are 20 people in a group. Out of them 7 people are non-vegetarian, 2 people are selected randomly. Write the probability distribution of non-vegetarian people.
OR
A chairman is biased so that he selects his relatives for a job 3 times as likely as others. If there are 3 posts for a job, find the probability distribution for selection of persons other than their relatives
Answer. Let x denote the number of non-vegetarian people selected at random.
Hence, x can take values 0, 1, 2.
P(x = 0) = P(No non-vegetarian people is selected)

Since the chairman is biased, so the probability that he selects his relatives for a job is 3 times as likely as others.
P(He selects his relative) = 3/4
P(He does not select his relative) = 1/4
P(x = 0) = P(All three are his relatives)