Please refer to Conic Sections MCQ Questions Class 11 Mathematics below. These MCQ questions for Class 11 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Conic Sections will help you to prepare for the exams and get more marks.
Conic Sections MCQ Questions Class 11 Mathematics
Please see solved MCQ Questions for Conic Sections in Class 11 Mathematics. All questions and answers have been prepared by expert faculty of standard 11 based on the latest examination guidelines.
MCQ Questions Class 11 Mathematics Conic Sections
Question. Let P be a variable point on the ellipse x2/25 + y2/16 = 1with foci at S and S¢. If A be the area of DPSS¢, then the maximum value of A is
(a) 24 sq units
(b) 12 sq units
(c) 36 sq units
(d) None of these
Answer
B
Question: A line meets the coordinate axes in A B and .A circle is circumscribed about the ∆OAB. The distances from the points A and Bof the side AB to the tangent at O are equal to m n and respectively. Then, the diameter of the circle is
(a) m (m+ n)
(b) n (m+n)
(c) m- n
d) None of these
Answer
D
Question: Let L1 be a straight line passing through the origin and L2 be the straight line x+ y = 1. If the intercepts made by the circle x2+y2-x+3y=0 on L1 and L2 are equal, then L1 can be represented by
(a) x+ y = 0
(b) x- y = 0
(c) 7x+y=0
(d) x- 7y=0
Answer
B
Question: Consider the following statements
I. Circle x2+y2-x-y-1=0 is completely inside the circle x2+y2– x+2y-7=0.
II. Number of common tangents of the circles x2+y2+14x+12y+21=0 and x2+y2+2x-4y-4=0 is 4.
Which of these is/are correct?
(a) Only I
(b) Only II
(c) Both I and II
(d) None of these
Answer
A
Question: The range of values of a such that the angle θ between the pair of tangents drawn from( a,0 ) to the circle x2+y2=1 satisfies π/2<θ π,is
(a) (1, 2)
(b) ( 1,√2)
(c) ( -√2,-1 )
(d) (-√2-1) ∪ (1,√2)
Answer
D
Question: Points (– 6, 0), (0, 6) and (–7, 7) are the vertices of ∆ABC. The incircle of the triangle has the equation
(a) x2+ y2 -9x -9y + 36 =0
(b) x2+ y2 +9x -9y + 36 =0
(c) x2+ y2 +9x +9y – 36 =0
(d) x2+ y2 +18x -18y +36 =0
Answer
B
Question: Two rods of lengths a b and slide along the x-axis and y-axis respectively in such a manner that their ends are concyclic. The locus of the centre of the circle passing through the end points is
(a) 4(x2+y2) =a2 +b2
(b) x2+y2 =a2 +b2
(c) 4(x2-y2) =a2 -b2
(d) x2-y2 =a2 -b2
Answer
C
Question: The equations of the sides AB, BC and CA of a ∆ ABC are x +y = 1, 4x -y + 4 = 0 and 2x+ 3y= 6.
Circles are drawn on AB BC , and CA as diameters. The point of concurrence of the common chord is
(a) centroid of the triangle
(b) orthocentre
(c) circumcentre
(d) incentre
Answer
B
Question: The set of values of c so that the equations y= |x|+c and x2+y2-8|x| -9 =0 have no solution, is
(a) (- ∞, -3) ∪ (3,∞)
(b) ( -3,3), )
(c) (- ∞,5√2) ∪ (5√2,∞ )
(d) (5,√2-4, ∞)
Answer
D
Question: Two points P Q and are taken on the line joining the points A( 0,0) and B ( ,3a,0) such that AP= PQ=QB.
Circles are drawn on AP, PQ, QB and as diameters.
The locus of the points, the sum of the squares of the tangents from which to the three circles is equal to b2 , is
(a) x2 +y2-3ax+2a2-b2=0
(b) 3(x2+y2)-9ax+8a2-b2=0
(c) x2+y2-5ax+6a2-b2=0
(d) x2+y2-ax-b2=0
Answer
B
Question: If OA OB and are equal perpendicular chord of the circles x2+ y2-2x + 4y= 0, then equations of OA and OB are (where, O is origin)
(a) 3x + y =0 and 3x-y =0
(b) 3x + y =0 and 3x-x =0
(c) x + 3y =0 and y-3x =0
(d) x + y = 0 and x-y= 0
Answer
B
Question: Equation of chord of the circle x2+y2-3x-4y-4=0, which passes through the origin such that the origin divides it in the ratio 4 1: ,is
(a) x = 0
(b) 24x+y=0
(c) 7x+24=0
(d) 7x-24y=0
Answer
B
Question: An isosceles right angled triangle is inscribed in the circle x2+y2= r2. If the coordinates of an end of the hypotenuse are ( a ,b), the coordinates of the vertex are
(a) (-a,-b)
(b) (b,- a)
(c) (b, a)
(d) (-b,- a)
Answer
B
Question: In a ∆ABC, right angled at A, on the leg AC as diameter, a semi-circle is described. If a chord joins A with the point of intersection D of the hypotenuse and the semi-circle, then the length of AC equal to
(a) ABx AD/√AB2+ AD2
(b) ABx AD/AB+ AD
(c) √ABx AD
(d) AB xAD/√AB2-AD2
Answer
D
Question: A rhombus is inscribed in the region common to the two circles x2+y2-4x-12=0 and x2+y2+4x -12=0 with two of its vertices on the line joining the centres of the circles. The area of the
rhombus is
(a) 8 √3 sq units
(b) 4 √3 sq units
(c) 6 √3 sq units
(d) None of these
Answer
A
Question: A straight line with slope 2 and y-intercept 5 touches the circle, x2+y2+16x+12y+c=0 at a point Q.Then, the coordinates of Q are
(a) (-6,11)
(b) (-9,-13)
(c) ( -10,10-15)
(d) (-6,-7)
Answer
D
Question: Two circles with radii a b and touch each other externally such that θ is the angle between the direct common tangents (a >b ≥2) , then
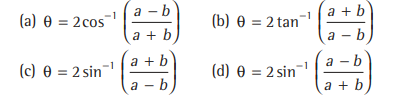
Answer
D
Question: A pair of tangents are drawn to a unit circle with centre at the origin and these tangents intersect at A enclosing an angle of 60°. The area enclosed by these tangents and the arc of the circle is
(a) 2/√3 −π/6
(b) √3 -π/3
(c) π/3- √3/6
(d) √3 (1- π/6)
Answer
B
Question: The equation of a line inclined at an angle π/4 to the x-axis, such that the two circles x2+y2=4, x2+y2-10x-14y+65=0 intercept equal lengths on it, is
(a) 2x-2y-3=0
(b) 2x-2y+3=0
(c) x-y+6=0
(d) x -y -6=0
Answer
A
Question: The equation of the tangents drawn from the origin
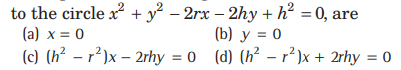
Answer
(A,C)
Question: The equation of a circle C1 is x2+y2=4. The locus of the intersection of orthogonal tangents to the circle is the curve C2 and the locus of the intersection of perpendicular tangents to the curve C2 is the curve C3 .Then,
(a) C3is a circle
(b) the area enclosed by the curve C3 is 8π
(c) C2 and C3 are circles with the same centre
(d) None of the above
Answer
(A,C)
Question: A (1/√2,1/√2) is a point on the circle x2+y2=1 and B is another point on the circle such that arc length AB =π/2 units. Then, coordinates of B can be
(a) (1/√2,-1/2)
(b) (-1/√2,1/√2
(c) (−1/√2,-1/√2)
(d) None of these
Answer
(A,B)
Question. Find the equation of the ellipse whose foci are (2, 3), (–2, 3) and whose semi-minor axis is of length 5.
(a) 5x2 + 9y2 + 54y + 36 = 0
(b) 5x2 + 9y2 – 54y + 36 = 0
(c) 5x2 + 9y2 – 54y – 36 = 0
(d) None of these
Answer
B
Question. The position of the point(4, – 3)relative to an ellipse x2/28 + y2/20 = 1 is
(a) inside
(b) on the ellipse
(c) outside
(d) cannot say
Answer
C
Question. A tangent at any point to the ellipse 4x2 + 9y2 = 36 is cut by the tangent at the extremities of the major axis at T and T’. The circle on T T’ as diameter passes through the point
(a) (0, √5 )
(b) ( √5, 0)
(c) (2, 1)
(d) (0, – √5 )
Answer
B
Question. If the normal at point P on the ellipse x2/a2 + y2/b2 = 1 meets the axes in R and S respectively, then PR : RS is equal to
(a) a : b
(b) a2 : b2
(c) b2 : a2
(d) b : a
Answer
C
Question. An ellipse is described by using endles string which is passed over two pins. If the axes are 6 cm and 4 cm, the necessary length of the string and distance between the pins respectively in cm, are
(a) 6, 2√5
(b) 6, √5
(c) 4, 2√5
(d) None of these
Answer
D
Question. The equation of the normal at the point (2, 3) on the ellipse 9x2 + 16y2 = 180 is
(a) 3y = 8x -10
(b) 3y – 8x + 7 = 0
(c) 8y + 3x + 7 = 0
(d) 3x + 2y + 7 = 0
Answer
B
Question. The curve represented by x = 3(cos t + sin t)and y = 4(cos t – sin t) is
(a) ellipse
(b) parabola
(c) hyperbola
(d) circle
Answer
A
Question. On the ellipse 4x2 + 9y2 = 1, the point at which the tangent is parallel to the line 8x = 9y, is
(a) (2/5 , 1/5)
(b) (-2/5 , 1/5)
(c) (-2/5 , -1/5)
(d) None of these
Answer
B
Question. An equation of the normal to the ellipse x2/a2 + y2/b2 = 1at the positive end of the latusrectum is
(a) x + ey + e3a = 0
(b) x – ey – ae3 = 0
(c) x – ey + e3a = 0
(d) x + ey – e3a = 0
Answer
B
Question. The circle x2 + y2 = c2 contains the ellipse x2/a2 + y2/b2 = 1, if
(a) c < a
(b) c < b
(c) c > a
(d) c > b
Answer
C
Question. If Qbe the point on the auxiliary circle corresponding to a point P on an ellipse. Then, the normals at P and Q meet on
(a) a fixed circle
(b) an ellipse
(c) a hyperbola
(d) None of these
Answer
A
Question. If the tangent line to an ellipse x2/a2 + y2/b2 = 1 1cuts intercepts h and k from axes, then a2/h2 + b2/k2 is equal to
(a) 0
(b) 1
(c) -1
(d) 2
Answer
B
Question. If the latusrectum of an ellipse is equal to half of minor axis, then its eccentricity is
(a) √15/3
(b) √15/2
(c) √15/6
(d) √15/4
Answer
D
Question. If the eccentricity of an ellipse is 5/8 and the distance between its foci is 10, then length of latus rectum of the ellipse is
(a) 39/7
(b) 39/4
(c) 39/5
(d) 39/8
Answer
B
Question. The locus of mid-points of chords of the ellipse x2/a2 + y2/b2 = 1 that touch the circle x2 + y2 = b2, is
(a) ( x2/a2 + y2/b2) = x2/a4 + y2/b4
(b) ( x2/a2 + y2/b2) =b2(x2/a4 + y2/b4)
(c) ( x2/a2 + y2/b2) = b2(x2/a4 + y2/b4)
(d) None of these
Answer
B
Question. The eccentric angles of the extremities of latusrectum of the ellipse x2/a2 + y2/b2 = 1 are given by
(a) tan-1 (± ac/b)
(b) tan-1 (± bc/a)
(c) tan-1 (± b/ae)
(d) tan-1 (± a/be)
Answer
C
Question. If the two tangents drawn to the ellipse x2/a2 + y2/b2 = 1 intersect perpendicularly at p, then locus of p is a circle x2 + y2 = a2 + b2. Then, the circle is called
(a) auxiliary circle
(b) director circle
(c) great circle
(d) None of these
Answer
B
Question. An ellipse is sliding along the coordinate axes. If the foci of the ellipse are (1, 1) and (3, 3), then area of the director circle of the ellipse is
(a) 2π sq units
(b) 4π sq units
(c) 6π sq units
(d) 8π sq units
Answer
D
Question. The eccentric angle of a point on the ellipse x2/6 + y2/2 = 1 whose distance from the centre of the ellipse is 2, is
(a) π/4
(b) 3π/2
(c) 5π/3
(d) 7π/6
Answer
A
Question. If e is eccentricity of ellipse x2/a2 + y2/b2 = 1 (a > b) and e’ is eccentricity of x2/a2 + y2/b2 = 1 (a < b) , then
(a) e = e’
(b) ee’ = 1
(c) 1/e2 + 1/(e’)2 = 1
(d) None of these
Answer
C
Question. If the normals atP(q)and Q(π/2 +θ) to the ellipse x2/a2 + y2/b2 = 1 meet the major axis at Gand grespectivel,y the PG2 + Qg2 is equal to
(a) b2(1- e2)(2 – e2)
(b) b2(e4– e2 + 2)
(c) a2(1+ e2)(2 + e2)
(d) b2(1+ e2)(2 + e2)
Answer
B
Question. If ax2 + by2 + 2hxy + 2gx + 2fy + c = 0 (abc + 2fgh – af2 – bg2 – ch2 ≠ 0) represents an ellipse, if
(a) h2 = ab
(b) h2 >ab
(c) h2< ab
(d) None of these
Answer
C
Question. The equation of the ellipse whose focus is (1, –1), the directrix of line x – y – 3 = 0 and eccentricity 1/2 is
(a) 7x2 + 2xy + 7y2 – 10x + 10y + 7 = 0
(b) 7x2 + 2xy + 7y2 + 7 = 0
(c) 7x2 + 2xy + 7y2 – 10x + 10y – 7 = 0
(d) None of the above
Answer
A
Question. The length of the latusrectum of the ellipse 3x2 + y2 = 12 is
(a) 4
(b) 3
(c) 8
(d) 4/√3
Answer
D
Question. If e is the eccentricity of the ellipse x2/a2 + y2/b2 = 1 (a < b), then
(a) b2 = a2 (1 -e2)
(b) a2 = b2(1 -e2)
(c) a2 = b2 = (e2 – 1)
(d) b2 = a2 = (e2 – 1)
Answer
B
Question. If Pis a point on the ellipse x2/16 + y2/25 = 1 1whose foci are S and S’, then PS + PS’ is equal to
(a) 8
(b) 7
(c) 5
(d) 10
Answer
D
Question. The locus of a point which moves such that the sum of its distances from two fixed points is always a constant, is
(a) a straight line
(b) a circle
(c) an ellipse
(d) a hyperbola
Answer
C
Question. Find the distance between the directrices of the ellipse x2/36 + y2/20 = 1.
(a) -18
(b) 18
(c) 17
(d) 19
Answer
B
Question. If equation of ellipse is x2/4 + y2/25 = 1 , then coordinate of the foci, eccentricity and the length of the latusrectum are respectively
(a) (0,± √21), √21/5 , 7/5
(b) (0,± √21), √21/5 , 8/5
(c) (0,± √21), √21/7 , 8/5
(d) None of the above
Answer
B
Question. If p, q are the segments of a focal chord of an ellipse b2x2 + a2y2 = a2b2, then
(a) a2( p+q ) = 2bpq
(b) b2( p+q ) = 2apq
(c) a( p+q ) = 2b2pq
(d) b( p+q ) = 2a2pq
Answer
B
Question. The equation of the ellipse whose foci are (±2, 0) and eccentricity 1/2, is
(a) x2/12 + y2/16 = 1
(b) x2/16 + y2/12 = 1
(c) x2/16 + y2/8 = 1
(d) None of these
Answer
B
Question. If vertices and foci of an ellipse are (0, ± 13) and (0, ± 5) respectively, then the equation of an ellipse is
(a) x2/144 + y2/169 = 1
(b) x2/169 + y2/144 = 1
(c) x2/12+ y2/13= 1
(d) None of these
Answer
A
Question. Find the equation of an ellipse, if major axis on the x-axis and passes through the points (4, 3) and (6, 2).
(a) x2/13+ y2/52= 1
(b) x2/40+ y2/10= 1
(c) x2/52+ y2/13= 1
(d) None of these
Answer
C
Question. The curve with parametric equations x = α + 5cos q, y = β + 4 sin q (where, q is parameter) is
(a) a parabola
(b) an ellipse
(c) a hyperbola
(d) None of these
Answer
B
Question. The curve represented by the equation 4x2 + 16y2 – 24x – 32y – 12 = 0 is
(a) a parabola
(b) a pair of straight lines
(c) an ellipse with eccentricity 1/2
(d) an ellipse with eccentricity √3/2
Answer
D
Question. In an ellipse length of minor axis is 8 and eccentricity is √5/3. The length of major axis is
(a) 6
(b) 12
(c) 10
(d) 16
Answer
B
Question. In an ellipse the distance between the foci is 8 and the distance between the directrices is 25. The length of major axis is
(a) 10√2
(b) 20√2
(c) 30√2
(d) None of these
Answer
A
Question. If the eccentricity of the two ellipse x2/169 + y2/25 = 1 and x2/a2 + y2/b2 = 1 are equal, then the value of a/b is
(a) 5/13
(b) 6/13
(c) 13/5
(d) 13/6
Answer
C
Question. The line x = at2 meets the ellipse x2/a2 + y2/b2 = 1 in the real points, if
(a) |t | < 2
(b) | t | ∈ 1
(c) |t | > 1
(d) None of these
Answer
B
Question. The angle between the pair of tangents drawn from the point (1, 2) to the ellipse 3x2 + 2y2 = 5 , is
(a) tan-1 (12 /5)
(b) tan-1 (6/ √5)
(c) tan-1(2 /√5)
(d) tan-1 (6 /5)
Answer
C
Question. If x cos α + y sin α = pis a tangent to the ellipse, then
(a) a2 sin α +b2 cosα = p2
(b) a2 + b2sin2α = p2 cosec2α
(c) a2 + cos2α = b2sin2α = p2
(d) None of the above
Answer
C
Question. Number of tangents from (7, 6) to ellipse x2/16 + y2/25 = 1 is
(a) 0
(b) 1
(c) 2
(d) None of these
Answer
C
Question. Let E be the ellipse x2/9 + y2/4 = 1 and C be the circle x2 + y2 = 9. Let P andQbe the points (1, 2) and (2, 1), respectively. Then,
(a) Q lies inside C but outside E
(b) Q lies outside both C and E
(c) P lies inside both Cand E
(d) P lies inside C but outside E
Answer
B
Question. The length of the axes of the conic 9x2 + 4y2 – 6x + 4y +1 = 0
(a) 1/2,9
(b) 3, 2/5
(c) 1, 2/3
(d) 3, 2
Answer
C
Question. The distance of the centre of ellipse x2 + 2y2 – 2 = 0 to those tangents of the ellipse which are equallyinclined from both the axes, is
(a) 3/√2
(b) √(3/2)
(c) √2/3
(d) √3/2
Answer
D
Question. The distances from the foci of P(x , y ) 1 1 on the ellipse x2/9 + y2/25 = 1 are
(a) 4 ± 5/4 y1
(b) 5 ± 4/5 x1
(c) 5 ± 4/5 y1
(d) None of these
Answer
C
Question. The sum of focal distance of any point on the ellipse with major and minor axes as 2a and 2b respectively, is equal to
(a) 2a
(b) 2 a/b
(c) 2 b/a
(d) b/a
Answer
A
Question. The locus of the point of intersection of the perpendicular tangents to the ellipse x2/9+ y2/4= 1 is
(a) x2 + y2 = 9
(b) x2 + y2 = 4
(c) x2 + y2 = 13
(d) x2 + y2 = 5
Answer
C
Question. The number of circle having radius 5 and passing through the points (– 2, 0) and (4, 0) is:
(a) One
(b) Two
(c) Four
(d) Infinite
Answer
B
Question. The locus of the centre of the circle which cuts off intercepts of length 2a and 2b from x-axis and y-axis respectively, is:
(a) x + y = a + b
(b) x2 + y2 = a2 + b2
(c) x2 − y2 = a2 − b2
(d) x2 + y2 = a2 − b2
Answer
C
Question. The equations to the tangents to the circle x2 + y2 − 6x + 4y =12 which are parallel to the straight line 4x+3y+5=0, are:
(a) 3x − 4y −19 = 0, 3x − 4y + 31 = 0
(b) 4x + 3y −19 = 0, 4x + 3y + 31 = 0
(c) 4x + 3y +19 = 0, 4x + 3y − 31 = 0
(d) 3x − 4y +19 = 0, 3x − 4y + 31 = 0
Answer
C
Question. The equations of any tangents to the circle x2 + y2 − 2x + 4y − 4 = 0 is:
(a) y = m(x −1) + 3 √1+ m2 − 2
(b) y = mx + 3 √1+ m2
(c) y = mx + 3 √1+ m2 − 2
(d) None of these
Answer
A
Question. If the distances from the origin to the centres of three circles x2 + y2 + 2λ1x −C2 = 0 ( 1,2,3) i x + y + λ x − c = i = are in G.P. then the lengths of the tangents drawn to them from any point on the circle x2 + y2 = c2 are in:
(a) (a)P.
(b) G.P.
(c) H.P.
(d) None of these
Answer
B
Question. The angle between a pair of tangents drawn from a point P to the circle x2 + y2 + 4x − 6 y + 9sin α +13cos α = 0 is 2α The equation of the locus of the point P is:
(a) x2 + y2 + 4x − 6y + 4 = 0
(b) x2 + y2 + 4x − 6y − 9 = 0
(c) x2 + y2 + 4x − 6y − 4 = 0
(d) x2 + y2 + 4x − 6y + 9 = 0
Answer
D
Question. The line lx + my + n = 0 is a normal to the circle x2 + y2 + 2gx + 2 fy + c = 0, if:
(a) lg+ mf − n = 0
(b) lg+ mf + n = 0
(c) lg−mf − n = 0
(d) lg−mf + n = 0
Answer
A
Question. If the circle x2 + y2 +2gx+2fy+c =0cuts each of the circle x2 + y2 −4 = 0, x2 + y2 −6x−8y+10=0 and x2 + y2 +2x−4y−2=0 at the extremities of a diameter, then
(a) c = −4
(b) g + f = c −1
(c) g2 + f2 − c =17
(d) g f = 6
Answer
All
Question. Equation of the circle having diameter x − 2 y + 3 = 0, 4 x − 3 y + 2 = 0 and radius equal to 1 is
(a) (x −1)2 + ( y − 2)2 =1
(b) (x − 2)2 + ( y −1)2 =1
(c) x2 + y2 − 2x − 4y + 4 = 0
(d) x2 + y2 −3x − 4y + 7 = 0
Answer
A,B
Question. Tangents are drawn from any point on the circle x2 + y2 = a2 to the circle x2 + y2 = b2 . If the chord of contact touches the circle x2 + y2 = c2 , a > b, then:
(a) a, b, c are in (a)P.
(b) a, b, c are in G.P.
(c) a, b, c are in H.P.
(d) a, c, b are in G.P.
Answer
B
Question. If two distinct chords, drawn from the point (p, q) on the circle x2 + y2 = px + qy (where p, q ≠ 0) are bisected by the x-axis, then:
(a) p2 = q2
(b) p2 = 8q2
(c) p2 < 8q2
(d) p2 > 8q2
Answer
D
Question. The common chord of the circle x2 + y2 + 4x +1 = 0 and x2 + y2 + 6x + 2y + 3 = 0 is:
(a) x + y +1 = 0
(b) 5x + y + 2 = 0
(c) 2x + 2y + 5 = 0
(d) 3x + y + 3 = 0
Answer
A
Question. The equation of the chord of the circle x2 + y2 = a having (x1 , y1 ) as its mid-point is:
(a) xy1 + yx1 = a2
(b) x1 + y1 = a
(c) xx1 + yy1 = x12 + y12
(d) xx1 + yy1 = a2.
Answer
C
Question. A circle of radius 5 units touches both the axes and lies in first quadrant. If the circle makes one complete roll on xaxis along the positive direction of x-axis, then its equation in the new position is:
(a) x2 + y2 + 20π x −10y +100π = 0
(b) x2 + y2 + 20π x +10y +100π = 0
(c) x2 + y2 − 20π x −10 y +100π = 0
(d) None of these
Answer
D
Question. If the line x + 2by + 7 = 0 is a diameter of the circle x2 + y2 − 6x + 2y = 0, then b = ?
(a) 3
(b) –5
(c) –1
(d) 5
Answer
B



