Please refer to Three Dimensional Geometry MCQ Questions Class 12 Mathematics below. These MCQ questions for Class 12 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Three Dimensional Geometry will help you to prepare for the exams and get more marks.
Three Dimensional Geometry MCQ Questions Class 12 Mathematics
Please see solved MCQ Questions for Three Dimensional Geometry in Class 12 Mathematics. All questions and answers have been prepared by expert faculty of standard 12 based on the latest examination guidelines.
MCQ Questions Class 12 Mathematics Three Dimensional Geometry
Question. If the straight lines x-1/k = y-2/2 = z-3/2 and x-2/3 = y-3/k = z-1/2 intersect at a point, then the integer is equal to
(a) –5
(b) 5
(c) 2
(d) –2
Answer
A
Question. The vector equation of the straight line passing through (1, 2, 3) and perpendicular to the plane

Answer
A
Question. The intersection point of the lines x-1/2 = y-2/3 = z-3/4 and x- y/5 = y-1/2=z is
(a) (1, 1, 1)
(b) (-1,-1,-1)
(c) (1,2,3)
(d) (2,2,2)
Answer
B
Question.
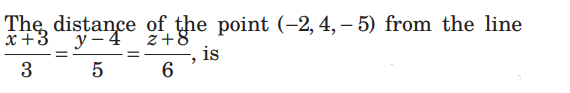
(a) √37/10
(b) 37/10
(c) 37/10
(d) None of these
Answer
A
Question. The coordinates of the foot of perpendicular drawn from the point A( 1,8,4) to the line joining the points B(0, 1 3) and C ( 2, 3,-1) is
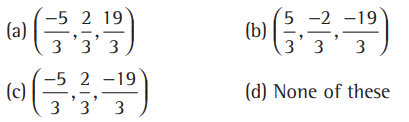
Answer
A
Question. The distance of the point( -15,-10) from the point of intersection of the line
(a) 11
(b) 12
(c) 11
(d) 13
Answer
D
Question. The image of the point (1 ,6 3 ) 1 in the line x/1= y-1/2 = z-2/3, is −
(a) (1, 6, 9)
(b) (1, 0, 7)
(c) (0, 2, 7)
(d) (7, 9, 0)
Answer
B
Question.
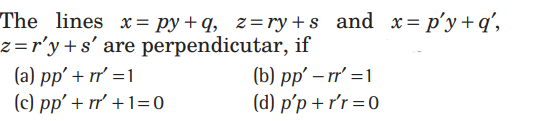
Answer
C
Question.
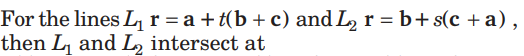
(a) a
(b) b
(c) a+ b c +
(d) a+ 2b
Answer
C
Question.

Answer
A
Question. Two lines x-1/2= y+1/3 = z-1/4 and x-3/1=y-k/2=z intersect at a point, if k is equal to
(a) 2/9
(b) 1/2
(c) 9/2
(d) 1/6
Answer
C
Question. A line with positive direction cosines passes through the point P(2,-1,2) and makes equal angles with the coordinate axes. The line meets the plane 2x+y+z=9 z + at point Q. The length of the line segment PQ equals
(a) 1
(b) √2
(c) √3
(d) 2
Answer
C
Question. The lines x/1=y/2= z/3 and x-1/-2=y-2/-4=z-3/-6 are
(a) interecting
(b) skew
(c) parallel
(d) coincident
Answer
D
Question. The length of the perpendicular drawn from ( 1,2,3) to the line x-6/3 = y-7/2 = z-7/-2 is
(a) 4
(b) 5
(c) 6
(d) 7
Answer
D
Question. The shortest distance between the lines x-3/3 = y-8/-1 = z-3/1 and x+3/-3 = y+7/2 = z-6/4 is
(a) √30
(b) 2 √30
(c) 5 √30
(d) 3 √30
Answer
D
Question. The coordinates of the point where the line through (3,-4,-5) and (2,-3,1) crosses the plane passing through three points (2, 2, 1), (3, 0, 1) and (4, 1, 0) −is,
(a) (1, 2, 7)
(b) (-1, 2, -7)
(c) (1, 2, 7)
(d) None of these
Answer
C
Question. The equation of the line passing through the point (3, 0, 1) and parallel to the planes x+ 2y = 0 and 3y- z=0,is
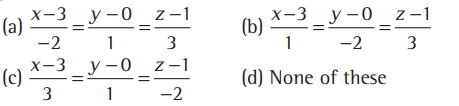
Answer
A
Question. If A(0,0,0), B (a,0,0),C(0,b,0) are the vertices of a tetrahedron, then the volume of tetrahedron is
(a) abc cu units
(b) abc/2cu units
(c) abc/3 cu units
(d) abc/6 cu units
Answer
D
Question. If l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines, then the direction cosines of the line perpendicular to both of these are
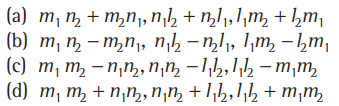
Answer
B
Question.
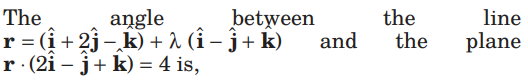
(a) 0
(b) π/2
(c) π
(d) None of these
Answer
D
Question. The angle between the lines whose direction cosines are given by 2l-m+2n=0,lm + mn + nl =0, is
(a) π/6
(b) π/4
(c) π/3
(d) π/2
Answer
D
Question. The x-coordinate of a point on the line joining the points Q(2, 2, 1) and R(5,1,-2 ) then its z-coordinate is
(a) 1
(b) −1
(c) 1/2
(d) 0
Answer
B
Question. The angle between the lines whose direction are given by l m+ n = 0 and l2 +m2 -n2=0 is
(a) π/6
(b) π/4
(c) π/3
(d) π/2
Answer
C
Question. A(3, 2, 0),B(5, 3, 2) and C( 9, 6, 3) − − are the vertices of a ∆ABC. If the bisector of ∠BAC meets BC at D, coordinates of D are
(a) (19/8.57/16,17/16)
(b) (-19/8, 57/16, 17/16)
(c) (19/8, -57/16, 17/16)
(d) (19/8, 57/16, -17/16)
Answer
A
Question. The angle between any two diagonals of a cube is
(a) sin−1 2/3
(b) cos−1 1/2
(c) cos−1 (1/√3)
(d) cos−1(1/3)
Answer
D
Question. The volume of the tetrahedron included between the plane 3x+ 4y- 5z- 60 = 0 and the coordinate planes is
(a) 60
(b) 600
(c) 720
(d) 400
Answer
B
Question. A line segment has length 63 and direction ratios are 3,- 2, 6. If the line makes an obtuse angle with x-axis,the components of the line vector are
(a) 27,-18,54
(b) −27 ,18, 54
(c) − 27, 18, -54
(d) 27,-18, -54
Answer
C
Question. Which one of the following planes contains the z-axis?
(a) x – z = 0
(b) z + y = 0
(c) 3x + 2y = 0
(d) 3x + 2z = 0
Answer
C
Question. The angle between a line whose direction ratios are in the ratio 2 : 2 : 1 and a line joining (3, 1, 4) to (7, 2, 12) is
(a) cos–1(2/3)
(b) cos–1(–2/3)
(c) tan–1(2/3)
(d) None of these
Answer
A
Question. Any three numbers which are proportional to the direction cosines of a line, are called.
(a) direction angles
(b) direction ratios
(c) another set of direction cosines
(d) None of the above
Answer
B
Question. The angle between the line x-2/a = y-2/b = z-2/c and the plane ax + by + cz + 6 = 0 is
(a) sin-1(1/√a2 + b2 + c2)
(b) 45°
(c) 60°
(d) 90°
Answer
D
Question. Under what condition do ⟨1/√2 , 1/2 , k⟩ represent direction cosines of a line?
(a) k = 1/2
(b) k = -1/2
(c) k = ± 1/2
(d) k can take any value
Answer
C
Question. The projection of the line segment joining the points (–1, 0, 3) and (2, 5, 1) on the line whose direction ratios are (6, 2, 3) is
(a) 6
(b) 7
(c) 22/7
(d) 3
Answer
C
Question. The length intercepted by a line with direction ratios 2, 7, –5 between the lines x-5/3 = y-7/-1 and x+3/-3 = y-3/2 = z-6/4 is
(a) √75
(b) √78
(c) √83
(d) None of these
Answer
B
Question. If the directions cosines of a line are k, k, k, then
(a) k > 0
(b) 0 < k < 1
(c) k = 1
(d) k = 1/√3 or -1/√3
Answer
D
Question. Two planes r . n1 = d1 and r . n2 = d2 are perpendicular to each other, if
(a) n1 = n2
(b) n1 is parallel to n2
(c) n1 . n2 = 0
(d) None of the above
Answer
C
Question. The projections of the segment PQ on the co-ordinate axes are –9, 12, –8 respectively. The direction cosines of the line PQ are
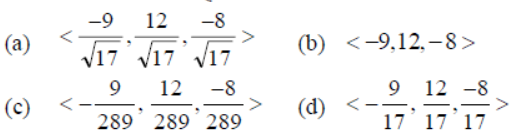
Answer
D
Question. If the equations of two lines l1 and l2 are given by r = a̅1+ λb̅1 and r = a̅2 + λb̅2 , where λ , μ are parameter then angle θ between them is given by
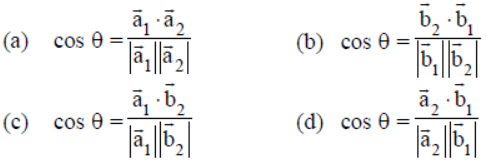
Answer
B
Question. The projections of a line segment on the coordinate axes are 12, 4, 3. The direction cosine of the line are:
(a) • 12/13 , • 4/13 , 3/13
(b) 12/13, • 4/13 , 3/13
(c) 12/13 , 4/13 , 3/13
(d) None of these
Answer
C
Question. The angle between two planes is equal to
(a) The angle between the tangents to them from any point.
(b) The angle between the normals to them from any point.
(c) The angle between the lines parallel to the planes from any point.
(d) None of these.
Answer
B
Question. Direction ratios of two lines are a, b, c and 1/bc , 1/ca , 1/ab , The lines are
(a) Mutually perpendicular
(b) Parallel
(c) Coincident
(d) None of these
Answer
B
Question. Consider the following statements
Statement I : The vector equation of a line passing through two points whose position vectors are a and b, is r = a + λ (b – a) ∀ λ ∈ R.
Statement II : The cartesian equation of a line passing through two points (x1, y1, z1) and (x2, y2, z2) is x-x1/x2-x1 = y-y1/y2-y1 = z-z1/z2-z1
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both statements are true
(d) Both statements are false
Answer
C
Question. The equation of the line passing through (1, 2, 3) and parallel to the planes r.(î – ĵ + 2k̂) = 5 and r. (3î + ĵ + k̂) = 6 is
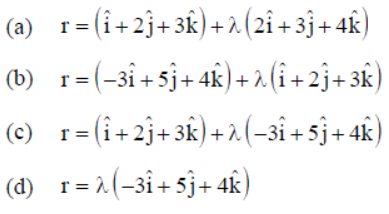
Answer
C
Question. A line makes angles of 45° and 60° with the positive axes of X and Y respectively. The angle made by the same line with the positive axis of Z, is.
(a) 30° or 60°
(b) 60° or 90°
(c) 90° or 120°
(d) 60° or 120°
Answer
D
Question. If vector equation of the line x-2/2 = 2y-5/-3 = z+1 , is

(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question. Consider the following statements
Statement I : The points (1, 2, 3), (–2, 3, 4) and (7, 0, 1) are collinear.
Statement II : If a line makes angles π/2 , 3π/4 and π/4 with X, Y and Z-axes respectively, then its direction cosines are 0, -1/√2 and 1/√2 .
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both statements are true
(d) Both statements are false
Answer
C
Question. Let the line x-2/3 = y-1/-5 = z+2/2 lie in the plane x + 3y –αz + β = 0. Then (α, β) equals
(a) (–6, 7)
(b) (5, –15)
(c) (–5, 5)
(d) (6, –17)
Answer
A
Question. The line which passes through the origin and intersect the two lines x-1/2 = y+3/4 = z-5/3 , x-4/2 = y+3/3 = z-14/4 , is
(a) x/1 = y/-3 = z/5
(b) x/-1 = y/3 = z/5
(c) x/1 = y/3 = z/-5
(d) x/1 = y/4 = z/-5
Answer
A
Question. The direction ratios of the line OP are equal and the length OP = √3 . Then the coordinates of the point P are :
(a) ( –1, – 1, –1)
(b) ( √3, √3, √3)
(c) ( √2, √2, √2)
(d) (2, 2, 2)
Answer
A
Question. Consider the following statements
Statement I : If a line in space does not pass through the origin, the direction cosines of the line does not exist.
Statement II : Two parallel lines have same set of direction cosines.
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both statements are true
(d) Both statements are false
Answer
B
Question. The ordered pair (λ, μ) such that the points (λ, μ, –6),(3, 2, –4) and (9, 8, –10) become collinear is
(a) (3, 4)
(b) (5, 4)
(c) (4, 5)
(d) (4, 3)
Answer
B
Question. The equation of the right bisector plane of the segment joining (2, 3, 4) and (6, 7, 8) is
(a) x + y + z + 15 = 0
(b) x + y + z – 15 = 0
(c) x – y + z – 15 = 0
(d) None of these
Answer
B
Question. The coordinates of a point on the line x+2/3 = y+1/2 = z-3/2 at a distance of 6/√2 from the point (1, 2, 3) is
(a) (56,,43, 111)
(b) (56/17 , 43/17 , 111/17)
(c) (2, 1, 3)
(d) (–2, –1, –3)
Answer
B
Question. If a plane passes through the point (1, 1, 1) and is perpendicular to the line x-1/3 = y-1/0 = z-1/4 , then its perpendicular distance from the origin is
(a) 3/4
(b) 4/3
(c) 7/5
(d) 1
Answer
C
Question. Which of the following are true?
I. If a, b and c are the direction ratios of a line, then ka, kb and kc is also a set of direction ratios.
II. The two sets of direction ratios of a line are in proportion.
III. There exists two sets of direction ratios of a line.
(a) I and II are true
(b) II and III are true
(c) I and III are true
(d) All are true
Answer
A
Question. If the plane x – 3y + 5z = d passes through the point (1, 2, 4), then the length of intercepts cut by it on the axes of X, Y, Z are respectively, is
(a) 15, –5, 3
(b) 1, –5, 3
(c) –15, 5, –3
(d) 1, –6, 20
Answer
A

