Please refer to Statistics MCQ Questions Class 11 Mathematics below. These MCQ questions for Class 11 Mathematics with answers have been designed as per the latest NCERT, CBSE books and syllabus issued for the current academic year. These objective questions for Statistics will help you to prepare for the exams and get more marks.
Statistics MCQ Questions Class 11 Mathematics
Please see solved MCQ Questions for Statistics in Class 11 Mathematics. All questions and answers have been prepared by expert faculty of standard 11 based on latest examination guidelines.
MCQ Questions Class 11 Mathematics Statistics
Question. If the standard deviation of x, x1,x2…xn, is 3.5, then the standard deviation of – 2x1 – 3 – 2x2 – 3 …, – 2xn – 3 is
(a) -7
(b) -4
(c) 7
(d) 1.75
Answer
C
Question. The mean deviation from mean of the observation a, a + d, a + 2d, …, a + 2nd is
(a) n(n+1)d2/3
(b) n(n+1)/2 .d2
(c) a +n(n+1)d2/2
(d) None of these
Answer
D
Question. The first of two samples has 100 items with mean 15 and SD = 3. If the whole group has 250 items with mean 15.6 and SD = √13.44, the SD of the second
group is
(a) 4
(b) 5
(c) 6
(d) 3.52
Answer
A
Question. If the mean of five observations x, x + 2, x + 4, x + 6 and x + 8 is 11, then the mean of last three observations is
(a) 13
(b) 15
(c) 17
(d) None of these
Answer
A
Question. The median of 19 observations of a group is 30. If two observations with values 8 and 32 are further included, then the median of the new group of 21 observations will be
(a) 28
(b) 30
(c) 32
(d) 34
Answer
B
Question. If a variable x takes values xi such that a ≤ x1≤ b for i = 1,2, … n, then
(a) a2≤ var(x)≤b2
(b) a ≤ var(x)≤b
(c) a2/4 ≤ var(x)
(d) (b-a)2 ≤ var(x)
Answer
D
Question. If the arithmetic mean of two unequal positive real numbers a and b (a > b) be twice as their geometric mean, then a : b is equal to
(a) (2 +√3) : (√2 +3)
(b) (2 -√3) : (√2 +3)
(c) (2 +√3) : (√2 -3)
(d) None of these
Answer
C
Question. Following is the statement of marks obtained by two students A and B in 10 examination papers.
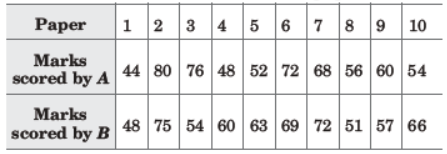
If the consistency of performance is the criterion for awarding a prize, find the prize winner among A and B.
(a) student A
(b) student B
(c) either students or A and B
(d) None of the above
Answer
B
Question. There are 60 students in a class. The following is the frequency distribution of the marks obtained by the students in a test

where, x is a positive integer. Find the mean and standard deviation of the marks.
(a) 2.9, 1.14
(b) 2.8, 1.12
(c) 2.8, 1.18
(d) None of these
Answer
B
Question. The variable x takes two values x1x2 and with frequencies f1f2 and , respectively. If σ denotes the standard deviation of x, then
(Diagram) (a,b)
Question. Which of the following is a correct statement?
(a) The sum of the deviations from arithmetic mean is zero
(b) Computation of arithmetic mean is based on all observations
(c) It gives no importance to extreme values
(d) None of the above
Answer
(A,B)
Question. If xi is replaced by xi’ , then new mean is
(a) x̄ –x1 + x1‘
(b) (n-1)x̄ + x1‘/n
(c) nx̄ – x1‘+ x1‘/n
(d) None of these
Answer
C
Question. If 5 is added in each observation, then the new variance is
(a) σ2
(b) σ2 + 5
(c) σ2 – 5
(d) None of these
Answer
A
Each of these questions contains two
statements : Statement I (Assertion) and Statement II (Reason). Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c) and (d) given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true.
Question. Suppose two groups of scores A and B are such that
A = (x, x + 2, x + 4) and B = (x – 2, x + 2, x + 6)
Statement I Group B has more variability than group A.
Statement II The value of mean for group B is more than that of group A.
Answer
C
Question. The algebraic sum of deviation from their mean is defined as i=1∑n (x1-x̄)
Statement I The algebraic sum of the deviations of
20 observations measured from 30 is 2. The mean value of the observations is 30.
Statement II The sum of deviation from their mean is zero.
Answer
D
Question. If n is a natural number, then
Statement I The mean of the squares of first n natural number is (n+)(2n+1) /6
Statement II ∑n = n(n+1)/2
Answer
B
Question. Standard deviation is not depend on change of origin.
Statement I The standard deviation of variable ax+b/c is |a/c|σ
Statement II The standard deviation of a linear equation is σ |coefficient of x|.
Answer
A
Question. Statement I If μ is the mean of a distribution, then ∑fi(yi – ∑) is equal to 0.
Statement II The mean of the square of first n natural numbers is 1/6 n(2n + 1).
Answer
C
Question. Statement I The variance of first n natural numbers is n2 – 1/12
Statement II The sum of first n natural numbers is n(n+1/2 and the sum of squares of first n natural numbers is n(n+1)(2n+1) /6
Answer
A
Question. If the mean deviations about the median of the numbers a, 2a, . . . , 5a is 50, then|a|is equal to
(a) 3
(b) 4
(c) 5
(d) 2
Answer
B
Question. For two data sets, each of size 5, the variance are given to be 4 and 5 and the corresponding means are given to be 2 and 4, respectively. The variance of the combined data set is
(a) 5/2
(b) 11/2
(c) 6
(d) 13/2
Answer
B
Question. If the mean deviation of number 1, 1 + d, 1 + 2d, . . . , 1 + 100d from their mean is 255,then the d is equal to
(a) 10.0
(b) 20.0
(c) 10.1
(d) 20.2
Answer
C
Question. Themean of the numbers a, b, 8, 5 and 10is 6 and the variance is 6.80. Then, which one of the following gives possible values of a and b?
(a) a = 3, b = 4
(b) a = 0, b = 7
(c) a = 5, b = 2
(d) a = 1, b = 6
Answer
A
Question. The average marks of boys in a class is 52 and that of girls is 42. The average marks of boys and girls combined is 50. The percentage of boys in the class is
(a) 40%
(b) 20%
(c) 80%
(d) 60%
Answer
C
Question. The minimum value of 2sin x + 2cos x is :
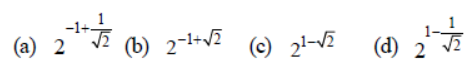
Answer
D
Question. If for some x ∈ R, the frequency distribution of the marks obtained by 20 students in a test is :
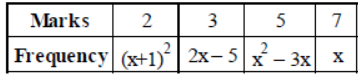
then the mean of the marks is :
(a) 3.2
(b) 3.0
(c) 2.5
(d) 2.8
Answer
D
Question. The mean and the median of the following ten numbers in increasing order 10, 22, 26, 29, 34, x, 42, 67, 70, y are 42 and 35 respectively, then
y/x is equal to:
(a) 9/4
(b) 7/2
(c) 8/3
(d) 7/3
Answer
D
Question. The mean of a set of 30 observations is 75. If each other observation is multiplied by a non- ero number l and then each of them is decreased by 25, their mean remains the same. The l is equal to
(a) 10/3
(b) 4/3
(c) 1/3
(d) 2/3
Answer
B
Question. Let the sum of the first three terms of an A. P, be 39 and the sum of its last four terms be 178. If the first term of this A.P. is 10, then the median of the A.P. is :
(a) 28
(b) 26.5
(c) 29.5
(d) 31
Answer
C
Question. A factory is operating in two shifts, day and night, with 70 and 30 workers respectively. If per day mean wage of the day shift workers is ₹54 and per day mean wage of all the workers is ₹60, then per day mean wage of the night shift workers (in ₹) is :
(a) 69
(b) 66
(c) 74
(d) 75
Answer
C
Question. In a set of 2n distinct observations, each of the observations below the median of all the observations is increased by 5 and each of the remaining observations is decreased by 3. Then the mean of the new set of observations:
(a) increases by 1
(b) decreases by 1
(c) decreases by 2
(d) increases by 2
Answer
A
Question. If the median and the range of four numbers {x, y, 2x + y, x – y}, where 0 < y < x < 2y, are 10 and 28 respectively, then the mean of the numbers is :
(a) 18
(b) 10
(c) 5
(d) 14
Answer
D
Question. The mean of a data set consisting of 20 observations is 40.
If one observation 53 was wrongly recorded as 33, then the correct mean will be :
(a) 41
(b) 49
(c) 40.5
(d) 42.5
Answer
A
Question. The median of 100 observations grouped in classes of equal width is 25. If the median class interval is 20 – 30 and the number of observations less than 20 is 45, then the frequency of median class is
(a) 10
(b) 20
(c) 15
(d) 12
Answer
A
Question. The frequency distribution of daily working expenditure of families in a locality is as follows:
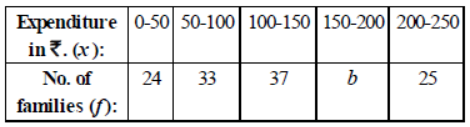
If the mode of the distribution is ₹140, then the value of b is
(a) 34
(b) 31
(c) 26
(d) 36
Answer
D
Question. The average marks of boys in class is 52 and that of girls is 42. The average marks of boys and girls combined is 50.
The percentage of boys in the class is
(a) 80
(b) 60
(c) 40
(d) 20
Answer
A
Question. Let x1, x2 , ………….. xn be n observations such that ∑X12 = 400 and ∑X1= 80 Then the possible value of n among the following is
(a) 15
(b) 18
(c) 9
(d) 12
Answer
B
Question. Let the observations xi(1 ≤ i ≤ 10) satisfy the equations,
i=1∑10 (xi – 5) = 10 and i=1∑10 (xi – 5)2 = 40 If μ and λ are the mean and the variance of the observations, x1 – 3, x2 – 3,…, x10 – 3, then the ordered pair (m, l) is equal to:
(a) (3, 3)
(b) (6, 3)
(c) (6, 6)
(d) (3, 6)
Answer
A
Question. The mean and the standard deviation (s.d.) of 10 observations are 20 and 2 respectively. Each of these 10 observations is multiplied by p and then reduced by q,
where p ≠ 0 and q ≠ 0. If the new mean and new s.d. become half of their original values, then q is equal to:
(a) –5
(b) 10
(c) –20
(d) –10
Answer
C
Question. If in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately
(a) 22.0
(b) 20.5
(c) 25.5
(d) 24.0
Answer
D
Question. The median of a set of 9 distinct observations is 20.5. If each of the largest 4 observations of the set is increased by 2, then the median of the new set
(a) remains the same as that of the original set
(b) is increased by 2
(c) is decreased by 2
(d) is two times the original median.
Answer
A
Question. In a class of 100 students there are 70 boys whose average marks in a sub ect are 75. If the average marks of the complete class is 72, then what is the average of the girls?
(a) 73
(b) 65
(c) 68
(d) 74
Answer
B
Question. The mean age of 25 teachers in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place. If now the mean age of the teachers in this school is 39 years, then the age (in years) of the newly appointed teacher is :
(a) 25
(b) 30
(c) 35
(d) 40
Answer
C
Question. The mean of the data set comprising of 16 observations is 16. If one of the observation valued 16 is deleted and three new observations valued 3, 4 and 5 are added to the data, then the mean of the resultant data, is:
(a) 15.8
(b) 14.0
(c) 16.8
(d) 16.0
Answer
B
Question. If = na , (n, a > 1), then the standard deviation of n observations x1, x2, …, xn is :
(a) a – 1
(b) n √a – 1
(c) √n(a – 1)
(d) √a – 1
Answer
D
Question. The mean and variance of 7 observations are 8 and 16, respectively. If five observations are 2, 4, 10, 12, 14, then the absolute difference of the remaining two observations is :
(a) 1
(b) 4
(c) 2
(d) 3
Answer
C
Question. If the mean and the standard deviation of the data 3, 5, 7, a,b are 5 and 2 respectively, then a and b are the roots of the equation : [Sep. 05, 2020 (II)]
(a) x2 -10x +18 = 0
(b) 2x2 – 20x +19 = 0
(c) x2 -10x +19 = 0
(d) x2 – 20x +18 = 0
Answer
C
Question. The mean and variance of 8 observations are 10 and 13.5, respectively. If 6 of these observations are 5, 7, 10, 12, 14, 15, then the absolute difference of the remaining two observations is :
(a) 9
(b) 5
(c) 3
(d) 7
Answer
D
Question. If a variance of the following frequency distribution :

is 50, then x is equal to _____________.
Answer
4
Question. For the frequency distribution :
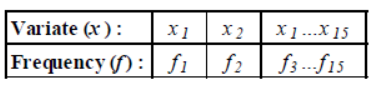
where 0 < x1 < x2 < x3 < … < x15 = 10 and i=1∑15 fi >0, the standard deviation cannot be :
(a) 4
(b) 1
(c) 6
(d) 2
Answer
C
Question. Let (1 10) ix ≤ i ≤ be ten observations of a random variable X.
If i=1∑10 (xi – p) =3 and i=1∑10 (xi – p)2 = 9 where 0 ≠ p∈R, then the standard deviation of these observations is :
(a) √3/5
(b) 4/5
(c) 9/10
(d) 7/10
Answer
C
Question. Let X = {x∈N : 1 ≤ x ≤17} and Y = {a x + b : x∈ X and a, b ∈R, a > 0}. If mean and variance of elements of Y are 17 and 216 respectively then a + b is equal to :
(a) 7
(b) –7
(c) –27
(d) 9
Answer
B
Question. If the variance of the terms in an increasing A.P., b1 , b2 , b3 , ….., b is 90, then the common difference of this A.P. is ___________.
Answer
3


