Please refer to Sequences and Series MCQ Questions Class 11 Mathematics below. These MCQ questions for Class 11 Mathematics with answers have been designed as per the latest NCERT, CBSE books and syllabus issued for the current academic year. These objective questions for Sequences and Series will help you to prepare for the exams and get more marks.
Sequences and Series MCQ Questions Class 11 Mathematics
Please see solved MCQ Questions for Sequences and Series in Class 11 Mathematics. All questions and answers have been prepared by expert faculty of standard 11 based on latest examination guidelines.
MCQ Questions Class 11 Mathematics Sequences and Series
Question: Which term of the AP, 19 18 1/5,18 2/5, , , . . . is the first negative term?
(a) 24
(b) 25
(c) 26
(d) 23
Answer
B
Question: If S1, S2 and S3 denote the sum of n1, n2 and n3 terms respectively of an AP, then
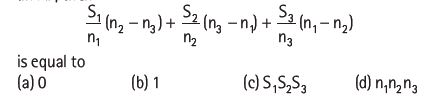
Answer
A
Question: If Sn denotes the sum of n terms of an AP, then Sn+3-3Sn+2+3Sn+1-Sn is equal to
(a) 0
(b) 1
(c)1/2
(d) 2
Answer
A
Question: If a2 b2, c2 are in AP, then a/b+c, b/c+a, c/a+b are in
(a) AP
(b) GP
(c) HP
(d) None of these
Answer
A
Question: The sum of all two digit numbers which when divided by 4, yield unity as remainder, is
(a) 1012
(b) 1201
(c) 1212
(d) 1210
Answer
D
Question:

Answer
B
Question: If 1, log , y x logz y, -15 logx z are in AP, then
(a) z3 =X
(b) x = y-1
(c) z-3 = y
(d) All of these
Answer
D
Question: A circle is completely divided into n sectors in such a way that the angles of the sectors are in AP. If the smallest of these angles is 8° and the largest is 72°, then the angle in the fifth sector is
(a) 40°
(b) 35°
(c) 42°
(d) 43°
Answer
A
Question: A farmer buys a used tractor of Rs. 12000. He pays `Rs. 6000 cash and agrees to pay the balance in annual instalment of Rs.500 plus 12% interest on the unpaid amount. The tractor cost for farmer is
(a) Rs.16680
(b) Rs. 16670
(c) Rs.16650
(d) None of these
Answer
A
Question:
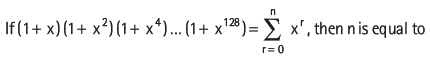
(a) 255
(b) 127
(c) 60
(d) None of these
Answer
A
Question: Let < an > be a GP such that a4/a6=1/4= and a2 + a5 = 216. Then, a1 is equal to
(a) 12 or 108/7
(b) 10
(c) 7 or54/7
(d) None of these
Answer
A
Question: Two numbers whose arithmetic mean is 34 and the geometric mean is 16, then the ratio of numbers is
(a) 5 or1/5
(b) 4 or1/4
(c) 2 or1/2
(d) 16 or1/16
Answer
D
Question: Let a1, a2, a3, …, be in AP and ap, aq, ar be in GP, then aq : ap is equal to
(a) r- p/q- p
(b) q-p/r- q
(c)r -q/q- p
(d) None of these
Answer
C
Question:

(a) xyz = x + y + z
(b) xz + yz = xy + z
(c) xy + yz = xz + y
(d) xy + xz = yz + x
Answer
A
Question:If the roots of equation (b2+ c2) x2 -2(a+b) cx +(C2 +a2) = 0 are equal, then
(a) a, b, c are in GP
(b) a, b, c are in AP
(c) a, c, b are in GP
(d) a, c, b are in AP
Answer
B
Question: If a, b, c are in GP, then b- a/b- c+b+a/b+ c is equal to
(a) b2– c2
(b) ac
(c) ab
(d) 0
Answer
A
Question:One side of an equilateral triangle is 24 cm. The mid-points of its sides are joined to form another triangle whose mid-points in term are joined to form still another triangle. The process continues indefinitely. The sum of perimeters of all the triangles is
(a) 144 cm
(b) 140 cm
(c) 145 cm
(d) None of the above
Answer
A
Question: 4 + 44 + 444 +Kis equal to

Answer
D
Question: The sum of sequence 0.15, 0.015, 0.0015, . . . , 20 terms is

Answer
A
Question: The sum 13/1+13+23/1+3+13+23+33/1+3+5+…to 16 terms is
(a) 246
(b) 646
(c) 446
(d) 746
Answer
C
Question: The sum of series 1+4/5+7/52+10/53+…∞ is
(a) 7/16
(b)5/16
(c)105/64
(d)35/16
Answer
D
Question: The sum 1+ 3 + 7 + 15 + 31+to n terms is
(a) 2n – 2- n
(b) 2n -1 – 1-n
(c) 2n+1-2-n
(d) None of these
Answer
C
Question:
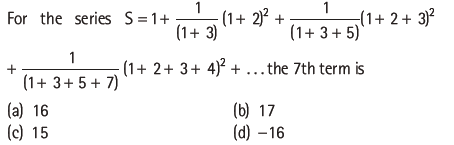
Answer
C
Question: The sum of the series 3×6 + 4×7 + 5×8 + … upto (n – 2) terms is

Answer
B
Question:
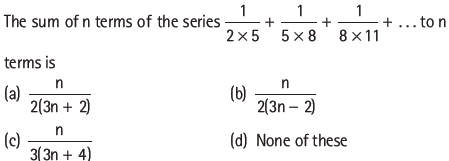
Answer
D
Question:

(a) ab
(b) -nab
(c) (n + 1)ab
(d) nab
Answer
D
Question: If roots of the equation x3 – 12x2 + 39 x – 28 = 0 are in AP, then its common difference is
(a) ± 1
(b) ± 2
(c) ± 3
(d) ± 4
Answer
C
Question: If 1/√b + √c, 1/√c + √a, 1/√a + √b are in A.P. then 9ax+1, 9bx+1, 9cx+1, x ≠ 0 are in :
(a) G.P.
(b) G.P. only if x < 0
(c) G.P. only if x > 0
(d) None of these
Answer
A
Question: The arithmetic mean of three observations is x. If the values of two observations are y, z; then what is the value of the third observation ?
(a) x
(b) 2x – y – z
(c) 3x – y – z
(d) y + z – x
Answer
C
Question: Let a1, a2, a3, ………..be the sequence, then the sum expressed as a1 + a2 + a3 + …… + an is called ……..
(a) Sequence
(b) Series
(c) Finite
(d) Infinite
Answer
B
Question: If the arithmetic, geometric and harmonic means between two positive real numbers be A, G and H, then
(a) A2 = GH
(b) H2 = AG
(c) G = AH
(d) G2 = AH
Answer
D
Question: A man saves Rs 135/- in the first year, Rs 150/- in the second year and in this way he increases his savings by Rs 15/- every year. In what time will his total savings be Rs 5550/-?
(a) 20 years
(b) 25 years
(c) 30 years
(d) 35 years
Answer
A
Question: If the sum of an infinitely decreasing GP is 3, and the sum of the squares of its terms is 9/2, then sum of the cubes of the terms is
(a) 107/12
(b) 105/17
(c) 108/13
(d) 97/12
Answer
C
Question: The sum of 11 terms of an A.P. whose middle term is 30,
(a) 320
(b) 330
(c) 340
(d) 350
Answer
B
Question: If an + bn / an – 1 + bn – 1 is the A.M. between a and b, then the value of n is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question: If G be the geometric mean of x and y, then 1/G2 − x2 + 1/G2 − y2 =
(a) G2
(b) 1/G2
(c) 2/G2
(d) 3G2
Answer
B
Question: The fourth, seventh and tenth terms of a G.P. are p, q, r respectively, then :
(a) p2 = q2 + r2
(b) q2 = pr
(c) p2 = qr
(d) pqr + pq + 1 = 0
Answer
B
Question: In a geometric progression consisting of positive terms, each term equals the sum of the next two terms. Then the common ratio of its progression equals
(a) √5
(b) 1/2(√5−1)
(c) 1/2(1−√5)
(d) 1/2√5.
Answer
B
Question: Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C D
(a) 2 1 4 3
(b) 2 4 1 3
(c) 3 4 1 2
(d) 3 1 4 2
Answer
C
Question: If f is a function satisfying f (x + y) = f (x) f (y) for all x, y ∈ N . such that f (1) = 3 and n∑x=1f(x) = 120, find the value of n.
(a) 2
(b) 4
(c) 6
(d) 8
Answer
B
Question: If x,y,z are in G.P. and ax = by = cz, then
(a) logb a = logac
(b) logcb = logac
(c) logb a = logcb
(d) None of these
Answer
C
Question: There are four numbers of which the first three are in G.P. and the last three are in A.P., whose common difference is 6. If the first and the last numbers are equal then two other numbers are
(a) –2, 4
(b) –4, 2
(c) 2, 6
(d) None of these
Answer
B
Question: If ax = by = cz, where a, b, c are in G.P. and a,b, c, x, y, z ≠ 0; then 1/x , 1/y , 1/z are in:
(a) A.P.
(b) G..P.
(c) H.P
(d) None of these
Answer
A
Question: The difference between any two consecutive interior angles of a polygon is 5°. If the smallest angle is 120°. The number of the sides of the polygon is
(a) 6
(b) 9
(c) 8
(d) 5
Answer
B
ASSERTION – REASON TYPE QUESTIONS
(a) Assertion is correct, reason is correct; reason is a correct explanation for assertion.
(b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, reason is incorrect
(d) Assertion is incorrect, reason is correct.
Question: Assertion: If a, b, c are in A.P., then b + c, c + a, a + b are in A.P.
Reason: If a, b, c are in A.P., then 10a, 10b, 10c are in G.P.
Answer
B
Question: Assertion: Sum to n terms of the geometric progression
x3, x5, x7, … (x ≠±1) is x3 (1−x2n)/(1−x2 )
Reason: If ‘a’ is the first term and r is common ratio of a G.P. then sum to n terms is given as
Sn = a(rn −1)/r−1 or = a(1−rn )/1−r if r ≠ 1.
Answer
A
Question: Assertion: The arithmetic mean (A.M.) between two numbers is 34 and their geometric mean is 16. The numbers are 4 and 64.
Reason: For two numbers a and b, A.M. = A = a + b/2
G.M = G = √ab.
Answer
A
Question: Assertion: If 2/3, k, 5/8 are in A.P, then the value of k is 31/48.
Reason: Three numbers a, b, c are in A.P. iff 2b = a + c
Answer
A
Question: Assertion: Sum of n terms of the A.P., whose kth term is 5k + 1, is n(5n+7)/2.
Reason: Sum of all natural numbers lying between 100 and 1000, which are multiples of 5, is 980.
Answer
C
Question: Assertion: : The sum of n terms of two arithmetic progressions are in the ratio (7n + 1) : (4n + 17), then the ratio of their nth terms is 7:4.
Reason: If Sn = ax2 + bx + c, then Tn = Sn – Sn–1
Answer
A
Question: Assertion: The 20th term of the series 2 × 4 + 4 × 6 + 6 × 8 + … + n terms is 1680.
Reason: If the sum of three numbers in A.P. is 24 and their product is 440. Then the numbers are 5, 8, 11 or 11, 8, 5.
Answer
B

