Please see Probability Exam Questions Class 9 Mathematics below. These important questions with solutions have been prepared based on the latest examination guidelines and syllabus issued by CBSE, NCERT, and KVS. We have provided Class 9 Mathematics Questions and answers for all chapters in your NCERT Book for Class 9 Mathematics. These solved problems for Probability in Class 9 Mathematics will help you to score more marks in upcoming examinations.
Exam Questions Probability Class 9 Mathematics
Very Short Answer Type Questions:
Question. A coin is tossed 1000 times with the following frequencies of Head and Tail :
Head : 455, Tail : 545
Compute the probability for the events
(i) getting a Head (ii) getting a Tail.
Ans. (i) Probability of getting Head = Number of head obtained/Total number of tossed coin
= 455/1000
= 0.455
(ii) Probability of getting Tail = Number of tail obtained/Total number of tossed coin
= 545/1000
= 0.545
Question. If the probability of an event is represented by p, then 0 ≤ p ≤ 1 is True/False ?
Ans. Probability of an event associated with a random experiment lies between 0 and 1 (both included). So given statement is true.
Question. When a coin is tossed, the probability of getting a head is ?
Ans. When a coin is tossed, total number of outcomes
= 2(Head or Tail)
∴ P(getting a head) = 1/2
Question. A coin is tossed 500 times with the following observations :
Head : 245 times, Tail : 255 times
The coin is tossed again. Find the probability of getting a head is ……………. .
Ans. Probability of getting a head = 245/500 = 0.49
Question. A die is thrown, what will be the probability of getting an even number ?
Ans. Favourable number of outcomes = 3 i.e., (2, 4, 6)
Total number of outcomes = 6
∴ Required probability = 3/6 = 1/2
Question. When a coin is tossed 500 times, the following outcomes were recorded :
Head : 270 times, Tail : 230 times
If a coin is tossed, what is the probability of getting a head ?
Ans. Required probability = 270/500 = 27/50
= 0·54
Short Answer Type Questions :
Question. Teachers and students are selected at random to make two teams of 30 members each on sports day to participate in the event of “tug of war”. The number of volunteers are as follows :
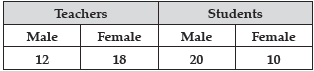
Find the probability that the person chosen at random
(i) is a male
(ii) is a female student.
Ans. Total number of volunteers = 12 + 18 + 20 + 10 = 60
(i) Total number of males = 12 + 20 = 32
P(volunteer is male) = 32/60 = 8/15
(ii) P(volunteer is female student) = 10/60 = 1/6
Question. The probability of guessing the correct answer to a certain question is x/3. If the probability of not guessing the correct answer is 5x/3, then find the value of x. A
Ans. P(E) + P(E’) = 1
x/3 + 5x/3 = 1
or, x + 5x/3 = 1
or, 6x/3 = 1
or, 2x = 1
or, x = 1/2
Question. In a cricket match, a batsman hits boundary in 20% of the balls he played. Find the probability that he did not hit a boundary.
Ans. Hits boundary = 20% of balls
Does not hit boundary = 80% of balls
∴ P(not hitting boundary) = 80 /100
= 4/5
Question. The weights of 60 persons in a group are given below :

Find the probability that a person selected at random has :
(i) weight less than 65 kg
(ii) weight between 61 and 64 kg
(iii) weight equal to or more than 64 kg
Ans. (i) P(Weight less than 65 kg) = 5 + 18 + 4 + 16 + 5 + 60
= 48/60 = 4/5
(ii) P(Weight between 61 kg and 64 kg) = 4 + 16/60 = 20/60 = 1/3
(iii) P(Weight equal to or more than 64 kg) = 5 + 12/60 = 17/60
Question. The given table shows the month of birth of 40 students.

(i) Find the probability that a student was born in the month with 31 days.
(ii) Find the probability that a student was born in the month of February.
Ans. (i) P(a student born in a month with 31 days)
= 3 + 2 + 5 + 2 + 6 + 4 + 4/40 = 26/40 = 0.65
(ii) P(student born in February)
= 4/40 = 0.1
Question. 1000 families with 2 children were selected randomly and following data was recorded :

If a family member is chosen at random, compute the probability that it has :
(i) 0 boys
(ii) 2 boys
Ans. (i) 0 boys [means family having two girls]
P(E) = 275/1000 = 11/40
(ii) 2 boys [means family having no girls]
P(E) =198/1000 = 99/500
Question. Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes :

Compute the probability of getting :
(i) at least 2 heads
(ii) all heads
Ans. (i) At least 2 heads P(E) = 200 – (42 + 78)/200
= 80/200 = 4/5
(ii) All heads P(E) = 35/200 = 7/40
Question. A survey of 500 families was conducted to know their opinion about a particular detergent powder. If 375 families liked the detergent powder and the remaining families disliked it, find the probability that a family chosen at random :
(i) likes the detergent powder.
(ii) does not like it.
Ans. (i) P(likes the detergent powder) = 375/500
= 3/4
(ii) P(does not like the detergent powder)
= 1 – P (likes the detergent powder)
= 1 – 3/4 = 1/4
Question. Three coins are tossed simultaneously 150 times with the following frequencies of different outcomes.

Compute the probability of getting.
(i) At least 2 tails
(ii) Exactly one tail
Ans. (i) At least 2 tails
[frequency of (number of 2 tails + number of 3 tails)]
P(E) = 32+63/150 = 95/150 = 19/30
(ii) Exactly one tail
P(E) = 30/150 = 1/5
Question. A box contains 50 bolts and 150 nuts. On checking the box, it was found that half of the bolts and half of the nuts are rusted. If one item is chosen at random, find the probability that it is rusted.
Ans. Number of bolts = 50
Number of nuts = 150
Total Number of bolts and nuts = 50 + 150 = 200
Half of them are rusted
or, 50/2 = 25 bolts
and 150/2 = 75 nuts are rusted
Total no. of rusted bolts and nuts = 25 + 75 = 100 Let E be the event of selecting one out of them which is rusted
∴ Number of favourable outcomes = 75 + 25 = 100
P(E) = 100/200 = 1/2
Question. A survey of 200 people was conducted about their preference of visiting various pavilions.

Find the probability that selected person visited :
(i) both Good living and Delhi pavilion.
(ii) only Defence pavilion.
(iii) only Toy pavilion
(iv) both Toy and Defence pavilion.
Ans. Total number of people = 200
(i) P(both good living and Delhi pavilion)
= 95 + 45/200
= 140/200 = 7/10 = 0.7
(ii) P(only defence pavilion)
= 20/200 = 1/10 = 0.1
(iii) P(only toy pavilion) = 40/200 = 1/5 = 0.2
(iv) P(both toy and defence pavilion) = 40 + 20/200 = 3/10 = 0.3
Question. In a one-day cricket Match, Sachin played 40 balls and hit 12 sixes and Saurav played 30 balls and hit 9 fours. Find the probability that Sachin will hit a six in the next ball and also find the probability that Saurav will not hit a four in the next ball.
Ans. Total number of balls faced by Sachin = 40
Number of balls on which he hit a six = 12
Let E1 be the event of hitting a six.
∴ Number of outcomes = 12
∴ P(E1) = 12/40 = 3/10 = 0.3
Now, Total number of balls faced by Saurav = 30
Let E2 be the event of Saurav did not hit a four
Number of outcomes = 30 – 9 = 21
P(E2) = 21/30 = 7/10 = 0.7
Question. Two coins are tossed simultaneously 500 times, following are the outcomes
No head = 100 times
One head = 200 times
Two heads = 200 times
If the two coins are simultaneously tossed again, compute the probability of obtaining :
(i) One Head
(ii) Two Heads
Ans. Total number of outcomes = 500
Let E1 and E2 be the events of one head and two heads respectively.
P(E1) = 200/500 = 2/5
P(E2) = 200/500 = 2/5
Long Answer Type Questions:
Question. The marks obtained by 30 students in a competitive exam are given below :

One student is chosen at random. Find the probability :
(i) that the student scored more than 65 marks.
(ii) that the marks scored by the students is an odd number.
Ans. Total number of students = 30
(i) Let E1 be the event of getting more than 65 marks
Number of favourable outcomes
= 2 + 3 = 8
Probability of the event, P(E1) = 5/30 = 1/6
(ii) Let E2 be the event of selecting a student having marks as odd no.
Number of favourable outcomes
= 4 + 6 + 2 = 12
Probability of an event i.e., P(E2)
= 12/30 = 2/5
Question. The heights of the students of a class is measured and recorded as given below :


A student is selected at random. Find the probability that height of the student is :
(i) more than 135 cm
(ii) at least 145 cm
(iii) less than 130 cm
(iv) 125 cm or more but less than 140 cm.
Ans. Total student = 7 + 7 + 11 + 3 + 5 + 9 + 8 = 50
(i) P(height of student is more that 135 cm) = 3 + 5 + 9 + 8/50 = 25/50 = 1/2
(ii) P(height of student is at least 145 cm) = 9 + 8/50
= 17/50
(iii) P(height of student is less than 130 cm) = 7 + 7/50
= 14/50 = 7/25
(iv) P(height of student is 125 cm or more but less than 140 cm) = 7 + 11 + 3/50 = 21/50
Question. In class IX of 50 students, second language opted by the students is as follows :
Sanskrit – 14
Japanese – 08
French – 12
Urdu – 6
Rest of them opted for German.
A student is selected at random. Find the probability that the student.
(i) opts for French
(ii) does not opts for Japanese
(iii) Either opts for Sanskrit or for German.
Ans. (i) Probability that a student selected opts
French language = 12/50
= 6/25
(ii) Probability that a student selected does not opt for
Japanese = 1 – selected student opts Japanese
= 1 − 8/50
= 42/50 = 21/25
(iii) Probability that selected student either opts for Sanskrit or for German = Probability. of student
opts Sanskrit + Probability of student opts. German
∴ Number of student who opted German
= 50 – (14 + 08 + 12 + 6)
= 50 – 40
= 10
∴ Probability that selected student either opt for Sanskrit or for German
= 14/50 + 10/50
= 24/50 = 12/25
