Please see Quadrilaterals Exam Questions Class 9 Mathematics below. These important questions with solutions have been prepared based on the latest examination guidelines and syllabus issued by CBSE, NCERT, and KVS. We have provided Class 9 Mathematics Questions and answers for all chapters in your NCERT Book for Class 9 Mathematics. These solved problems for Quadrilaterals in Class 9 Mathematics will help you to score more marks in upcoming examinations.
Exam Questions Quadrilaterals Class 9 Mathematics
Very Short Answer Type Questions:
Question. In an equilateral triangle ABC, D and E are the mid-points of sides AB and AC respectively, then find the length of DE.
Ans.
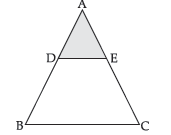
Since, D and E are mid-points of sides AB and AC respectively. So, by mid-point theorem, DE = 1/2 BC.
Question. The angles of a quadrilateral are in the ratio 2 : 3 : 6 : 7. Find the largest angle of the quadrilateral.
Ans. Let the angles of the quadrilateral be 2x°, 3x°, 6x°,7x°.
∴ 2x° + 3x° + 6x° + 7x° = 360° [Angle sum property of quadrilateral]
or, 18x° = 360°
or, x° = 20°
∴ Largest angle = 7x° = 7 × 20° = 140°
Question. Two consecutive angles of a parallelogram are in the ratio 1 : 3, then what will be the smaller angles ?
Ans. Let the consecutive angles be x° and 3x°.
∴ x° + 3x° = 180°
or, 4x° = 180°
or, x° = 45°
∴ Smaller angle = x°
= 45°
Question. D, E, F are the mid-points of sides BC, CA and AB of ΔABC. If perimeter of ΔABC is 12·8 cm, then find perimeter of ΔDEF.

Ans. Given, perimeter of ΔABC = 12·8 cm
∴ Perimeter of ΔDEF = 1/2(perimeter of ΔABC)
= 12.8/2 cm
= 6·4 cm
Short Answer Type Questions:
Question. In a parallelogram ABCD if ∠A = 115°, find ∠B, ∠C and ∠D.
Ans.
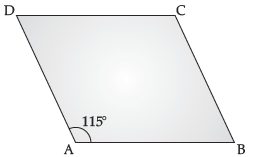
In a ||gm,
Consecutive angles are supplementary
∴ ∠A + ∠B = 180°
115° + ∠B = 180°
∠B = 180° – 115°
∴ ∠B = 65°
∠A = ∠C = 115°
(Opposite angles are equal in ||gm)
∠B = ∠D = 65°
Question. The angles of a quadrilateral are 4x°, 7x°, 15x° and 10x°. Find the smallest and largest angles of the quadrilateral.
Ans. Sum of the angles of a quadrilateral is 360°.
∴ 4x° + 7x° + 15x° + 10x° = 360°
or, 36x° = 360°
or, x° = 10°
∴ Smallest angle = 4x° = 4 × 10° = 40°
Largest angle = 15x° = 15 × 10° = 150°
Question. The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Ans. Let the measure of the angles be 3x°, 5x°, 9x° and 13x°, Then,
3x° + 5x° + 9x° + 13x° = 360° [Angle sum property of quadrilateral]
or, 30x° = 360°
x = 12°
∴ Angles are : 36°, 60°, 108°, 156°.
Question. ABCD is a rhombus. Show that the diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Ans. Given, ABCD is a rhombus.
So, AB = BC = CD = AD
To prove :
∠BAC = ∠DAC and ∠DCA = ∠BCA
In ΔADC and ΔABC,
AB = AD (Given)
CD = CB (Given)
AC = AC (Common)
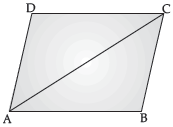
So, ΔADC ≅ ΔABC (SSS Congruence Rule)
So, ∠DAC = ∠BAC (c.p.c.t.)
∠DCA = ∠BCA (c.p.c.t.) Hence Proved.
Question. The angles A, B, C and D of a quadrilateral ABCD are in the ratio 2 : 4 : 5 : 7. Find the measures of these angles. What type of quadrilateral is it ? Give reasons.
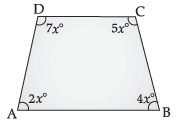
Ans. Let the measures of the angles be 2x°, 4x°, 5x° and 7x°.
∴ 2x° + 4x° + 5x° + 7x° = 360° (Angle sum property)
or, 18x° = 360°
or, x° = 20°
∠A = 40°
∠B = 80°
∠C = 100°
∠D = 140°
As ∠A + ∠D = 180° and ∠B + ∠C = 180°
or, CD || AB
Hence, ABCD is a trapezium. 1
Question. Diagonal AC of a parallelogram ABCD bisects ∠A. Show that :
(i) it bisects ∠C also
(ii) ABCD is a rhombus
Ans.
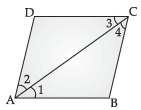
(i) AB = CD, AD || BC
∠1 = ∠3 …(i)
∠2 = ∠4 (Alt. interior angles)
But ∠1 = ∠2 …(ii) (Given, diagonal AC bisects ∠A)
∠3 = ∠4 (On comparing eqn. (i) and eqn. (ii))
(ii) AC bisects ∠C, Proved
As, ∠1 = ∠2 = ∠3 = ∠4
Hence, ∠1 = ∠4
AB = BC (sides opp. to equal angles)
Hence, ABCD is a rhombus (in a parallelogram if one pair of adjacent sides are equal then it is a rhombus)
Question. Two parallel lines l and m are intersected by a transversal ‘t’. Show that the quadrilateral formed by bisectors of interior angles is a rectangle.
Ans. Given : Two parallel lines l and m are intersected by a transversal line t at the points A and C respectively. The bisectors of ∠PAC and ∠QCA meet at B and bisectors of ∠SAC and ∠RCA meet at D.
To Prove : ABCD is a rectangle.
Proof : We know that a rectangle is a parallelogram with one angle 90°. First we will prove ABCD is a parallelogram.
For l || m & transversal t.
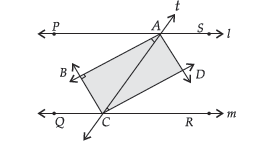
∠PAC = ∠ACR (Alternate angles)
So, 1/2 ∠PAC = 1/2 ∠ACR
i.e., ∠BAC = ∠ACD (Given, AB bisects ∠PAC and CD bisects ∠ACR)
For lines AB and DC with AC as transversal, ∠BAC and ∠ACD are alternate angles, and they are equal So, AB || DC.
Similarly, for lines BC and AD with AC as transversal, ∠BAC and ∠ACD are alternate angles, and they are equal
So, BC || AD
Now, in quadrilateral ABCD,
AB || CD and BC || AD
∴ ABCD is a parallelogram.
Also, for line l,
∠PAC + ∠CAS = 180° (Linear pair)
1/2 ∠PAC + 1/2 ∠CAS = 1/2 ×180°
∴ ∠BAC + ∠CAD = 90° (AB is bisector of ∠PAC and AD is bisector of ∠CAS)
or, ∠BAD = 90°
So, ABCD is a parallelogram in which one angle is 90°.
∴ ABCD is a rectangle.
Question. If angles of a quadrilateral are in ratio 1 : 2 : 3 : 4. Find the measure of all the angles of a quadrilateral.
Ans. Let the measure of the angles be x°, 2x°, 3x° and 4x° then,
x° + 2x° + 3x° + 4x° = 360°
or, x = 36°
∴ Angles of quadrilateral are 36°, 72°, 108° and 144°
Question. The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle is 50°. Find the angles of a parallelogram.
Ans. AM ⊥ DC, AN ⊥ BC
In quadrilateral AMCN,
∠A + ∠M + ∠C + ∠N = 360°
or ∠A + 90° + ∠C + 90° = 360°
∴ ∠A + ∠C = 180°
or, 50° + ∠C = 180° or, ∠C = 130°
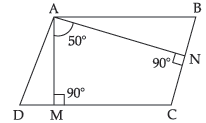
In parallelogram, ∠A = ∠C = 130°
∠B = ∠D = 180° – 130°
= 50°
Long Answer Type Questions :
Question. In the given figure, ABC is an isosceles triangle in which AB = AC, AD bisects the exterior angle PAC and CD || AB. Show that :
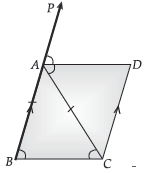
(i) ∠DAC = ∠BCA, and
(ii) ABCD is a parallelogram.
Ans. (i) ΔABC is an isosceles triangle.
or, ∠ABC = ∠BCA
∠PAC = ∠ABC + ∠BCA (Sum of two interior angles is equal to exterior angle)
= 2∠BCA …(i)
AD bisects ∠PAC or, ∠PAC = 2∠DAC …(ii)
From (i) and (ii), ∠BCA = ∠DAC
(ii) ∠BCA = ∠DAC (Proved above)
These are alternate angles when lines BC and AD are intersected by AC
or, BC || AD,
Also, BA || CD (Given)
∴ ABCD is a parallelogram. Hence Proved
Question. ABCD is a quadrilateral in which the bisectors of ∠A and ∠C meet DC produced at Y and BA produced at X respectively. Prove that, ∠X + ∠Y = 1/2 (∠A + ∠C)
Ans.
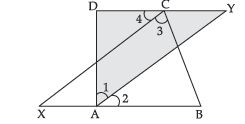
∠1 = ∠2 = 1/2 ∠A (∴ AY is bisector of ∠A)
∠3 = ∠4 = 1/2 ∠C (∴ CX is bisector of ∠C)
In ΔCXB,
∠3 + ∠X + ∠B = 180° …(i) (Angle sum property of a D)
In ΔDAY,
∠1 + ∠Y + ∠D = 180° …(ii) (Angle sum property of a D)
Adding (i) and (ii),
∠3 + ∠X + ∠B + ∠1 + ∠Y + ∠D = 180° + 180°
i.e., ∠X + ∠Y + ∠3 + ∠1 + ∠B + ∠D = 360°
i.e., ∠X + ∠Y + 1/2 ∠C + 1/2 ∠A + ∠B + ∠D = 360° …. (iii)
But, ∠A + ∠B + ∠C + ∠D = 360° … (iv) (Angle sum property of a quadrilateral)
From (iii) and (iv),
∠X + ∠Y + 1/2 ∠C + 1/2 ∠A + ∠B + ∠D
= ∠A + ∠B + ∠C + ∠D
i.e., ∠X + ∠Y = ∠A – 1/2 ∠A + ∠C – 1/2 ∠C
= 1/2 ∠A + 1/2 ∠C
∴ ∠X + ∠Y = 1/2 (∠A + ∠C)
Hence Proved
Question. Prove that the opposite angles of an isosceles trapezium are supplementary.
Ans. In trapezium ABCD,
AB || DC and AD = BC
Through C, draw
CE || DA
Here, DC || AE and CE is transversal.
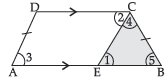
∴ ∠1 = ∠2 (Alternate angles)
Also, ∠3 = ∠1 (Corresponding angles)
∠2 = ∠3 = ∠1
∴ ∠2 + ∠3 = 2 ∠1
∴ ∠A + ∠C = ∠3 + ∠2 + ∠4
= 2 ∠1 + ∠4 …(i)
Also, ∠1 = ∠5
[AECD is a parallelogram ⇒ DA = CE = CB]
∠A + ∠C = ∠1 + ∠4 + ∠5 = 180°
Similarly, we can show that ∠B + ∠D = 180°
Hence, the opposite angles of an isosceles trapezium are supplementary. Hence Proved
