Please see Surface areas and Volumes Exam Questions Class 9 Mathematics below. These important questions with solutions have been prepared based on the latest examination guidelines and syllabus issued by CBSE, NCERT, and KVS. We have provided Class 9 Mathematics Questions and answers for all chapters in your NCERT Book for Class 9 Mathematics. These solved problems for Surface areas and Volumes in Class 9 Mathematics will help you to score more marks in upcoming examinations.
Exam Questions Surface areas and Volumes Class 9 Mathematics
Very Short Answer Type Questions:
Question. Two cylinders have bases of same size. The diameter of each is 7 cm. If one of the cylinder is 10 cm high and the other is 20 cm high, then find the ratio of their volumes.
Ans. Let r denotes the radius of both cylinders and h and h’ be their heights respectively.
Ratio of their volumes = 4πr2h/4πr2h’ = h/h’ = 10/20
= 1 : 2.
Question. Find the volume of a right circular cone with radius 6 cm and height 7 cm.
Ans. Volume of right circular cone = 1/3πr2h
= 1/3 × 22/7 × (6)2 × 7 = 1/3× 22/7 × 36 × 7
= 264 cm3.
Question. How many faces does a right circular cylinder have ?
Ans. 3
Question. Find the capacity of a tank of dimensions 8 cm × 6 cm × 2.5 cm.
Ans. Capacity of the tank = 120 cm3
Detailed Solution :
Capacity of the tank = length × breadth × height
= 8 cm × 6 cm × 2.5 cm
= 120 cm3.
Question. Calculate the volume of a cuboid whose dimensions are 3.6 cm, 8.2 cm and 11 cm.
Ans. Volume of cuboid = length × breadth × height
= 3.6 × 8.2 × 11
= 324.72 cm3.
Short Answer Type Questions:
Question. A rectangular piece of paper is 22 cm long and 10 cm wide. A cylinder is formed by rolling the paper along its length. Find the volume of the cylinder.
Ans.

2πr = 22
2 × 22/7 × r = 22
r = 7/2
V = πr2h
= 22/7 × 7/2 × 7/2 × 10
= 385 cm3
Question. The length, breadth and height of a room are 5 m, 4 m and 3 m. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs 7.50 per m2.
Ans. Given, l = 5 m, b = 4 m, h = 3 m.
Area to be painted = Area of walls + Area of ceiling
= 2h(l + b) + l × b
= 2 × 3(9) + 20
= 54 + 20 = 74 m2
Cost of painting 1 m2= Rs 7.50
∴ Cost of painting 74 m2= 74 × 7.50
= Rs 555
Question. The total surface area of a solid right circular cylinder is 1540 cm2. If the height is four times the radius of the base, then find the height of the cylinder.
Ans. Given, T.S.A. = 1540 cm2
∴ 2πr(h + r) = 1540 cm2
Also, h = 4r
∴ 2πr (4r + r) = 1540
or, 2π × 5r2 = 1540
or, r2 = 1540 × 7/2 × 5 × 22
or, r2 = 49
or, r = 7 cm
Now h = 4r
or, h = 28 cm.
Question. A solid piece of metal, cuboidal in shape, with dimensions 24 cm, 18 cm and 4 cm is recast into a cube. Calculate the lateral surface area of the cube.
Ans. Volume of cuboid = lbh
= 24 × 18 × 4
= 1728 cu.cm.
Edge of a cube = 3√1728
= 12 cm
LSA = 4a2
= 4 × 12 × 12
Question. The internal and external diameters of a hollow hemispherical vessel are 24 cm and 25 cm respectively. If the cost of painting 1 cm2 of the surface area is Rs 0.05, find the total cost of painting the vessel all over.
Ans. Internal radius (r) = 12 cm
External radius (R) = 12.5 cm
T.S.A = 2πr2+ 2πR2 + π(R2– r2)
= 2π(r2+ R2) + π(R – r)(R + r)
= 2π (144 + 156.25) + π (12.5 + 12)( 12.5 – 12)
= (600.50 + 12.25) × 22/7
= 1925.79 cm2
Cost of painting 1925.79 cm2 at the rate of Rs 0.05/cm2
= 1925.79 × 0.05
= Rs 96.29.
Question. Find the radius of the base of a right circular cylinder whose curved surface area is 2/3 of the sum of the surface areas of two circular faces. The height of the cylinder is given to be 15 cm.
Ans. Given, h = 15
C.S.A. = 2/3 (Sum of circular faces)
2πrh = 2/3(2πr2)
15 = 2/3r
45/2 = r
r = 22.5 cm.
Question. A dome of a building is in the form of a hemisphere From inside, it was white washed at the cost of Rs 997.92. If the cost of white washing is 400 paise per square meter, find the volume of air inside the dome. (Take π = 22/7)
Ans. Cost of white washing hemispherical
dome = Rs 997.92
Cost of white washing per square meter
= 400 paise = Rs 4
∴ CSA = 997.92 ÷ 4 = 249.48 m2
2πr2 = 249.48
2 × 22/7 × r2 = 249.48
or, r2 = 39.69
or, r = 6.3 m
∴ Volume of air inside it
= 2/3πr3
= 2/3 × 22/7 × 6.3 × 6.3 × 6.3
= 523.90 m3.
Question. The total surface area of a solid hemisphere is 5940 cm2. Find the diameter of the hemisphere.
Ans. Let the radius of hemisphere be r
∴ 3πr2 = 5940
or, r2 = 5940 × 7/3 × 22 = 630
or, r = √630 or 3√70 cm.
So, d = 2r = 6√70 cm.
Hence diameter of the hemisphere is 6√70 cm.
Question. The surface area of a cuboid is 1372 cm2. If its dimensions are in the ratio 4 : 2 : 1, find its length.
Ans. 2(lb + bh + hl) = 1372
l = 4x, b = 2x, h = x
2(4x × 2x + 2x × x + 4x × x) = 1372
or, 2(8x2 + 2x2 + 4x2) = 1372
or, 28x2 = 1372
or, x2 = 49
or, x = 7 cm
∴ Length = 4 × 7 = 28 cm.
Question. A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How many litres of water can it hold ?
Ans. Cuboidal water tank
length = 6 m
width = 5 m
height = 4.5 m
Volume of tank = length × width × height
= 6 × 5 × 4.5 m3
= 135 m3
= 135 × 1000 litre
(1 m3= 1000 litre)
∴ Volume of water = 135000 litre
or Capacity of tank = 135000 litre = 135 kl
Long Answer Type Questions:
Question. The frame of a lampshade is cylindrical in shape. It has base diameter 28 cm and height 17 cm. It is to be covered with a decorative cloth. A margin of 2 cm is to be given for folding it over top and bottom of the frame. If 1/12 of cloth is wasted in cutting and pasting, find how much cloth is required to be purchased for covering the frame.
Ans. Base diameter = 28 m
Base radius = 28/2 = 14 cm
Height of cloth required = 17 + 2 + 2 = 21 cm
Area of cloth required = Curved surface area of cylinder of radius 14 cm and height 21 cm
= 2πrh
= 2 × 22/7 × 14 × 21
= 1848 cm2
Let A sq. cm of cloth be purchased .
So, wastage of cloth for cutting and pasting
= A/12 cm2
Area of cloth actually used = A − A/12 = 11/12 A cm2
Area of cloth actually used = Area of cloth required
or, 11/12A = 1848
or, A = 1848 × 12/11 = 2016 cm2
Question. A pen stand is cylindrical in shape with the base radius 3.5 cm and height 10.5 cm. How much card board will be required to make 25 such pen stand ? Also, find volume of 1 pen stand.
Ans. Given, base radius of cylinder r = 3.5 cm
Height of cylinder h = 10.5 cm
Amount of card board required to make one pen stand
= πr(r + 2h)
One pen stand = 22/7 × 3.5(3.5 + 21)
= 22 × 0.5(24.5)
= 269.5 cm2
Amount of card board required to make 25 pen stand
= 269.5 × 25
= 6737.5 cm2
1 pen stand, then for 25 stands = 25 × 308
= 7700 cm2
Volume of 1 pen stand = πr2h
= 22/7 × 3.5 × 3.5 × 10.5
= 404.25 cm3.
Question. A right angled DABC with sides 3 cm, 4 cm and 5 cm is revolved about the fixed side of 4 cm. Find the volume of the solid generated. Also, find the total surface area of the solid.
Ans.
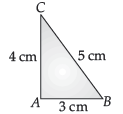
rcone = 3 cm
hcone = 4 cm
lcone = 5 cm

Above given cone is formed with radius 3 cm, height 4 cm and slant height 5 cm when revolved about the fixed side of 4 cm.
V = 1/3πr2h
= 1/3 × 22/7 × (3) × (3) × (4)
= 37.71 cm3
Total surface area = πrl + πr2 = πr(l + r)
= 22/7 × 3(5 + 3)
= 75.43 cm2.
Question. A cylindrical bowl of internal diameter 18 cm and height 15 cm is full of liquid. The whole of the liquid is to be filled in small cylindrical bottles of diameter 3 cm and height 4 cm, Each bottle is sold for Rs 5, then find the amount earned.
Ans. Volume of liquid = πr2h
Given, r = 18/2 = 9 cm
and h = 15 cm
∴ Volume of liquid = π(9)2 15
= 1215 π cm3
Also, radius of small bottle
(r’) = 3/2 = 1.5 cm
and height of small bottle
(h’) = 4 cm
∴Volume of small bottle = π(r’)2h’
= π(1.5)24
= 9π
Number of bottles = 1215π/9π = 135
∴ Amount earned = 135 × 5 = Rs 675
Question. An open box is made of wood 3 cm thick. Its external dimensions are 1.4 m, 1.1 m and 0.8 m. Find the cost of painting the outer surface of box at 75 paise per 100 cm2.
Ans. l = 140 cm
b = 110 cm
h = 80 cm
Surface area of open box = lb + 2(bh + hl)
Cost of painting box = Rs 75/100 × 100 [154 + 2(88 + 112)] × 100
= Rs 3/4 [554] = Rs 3(138.5)
= Rs 415.5
Question. Calculate the curved surface area of a cone whose radius of base and height are in the ratio 5 : 12 and its volume is 2512 cu. cm.
Ans. Let r = 5x, h = 12x
Given : 1/3πr2h = 2512 cu. cm
∴ 1/3π × 3.14(5x)2 × 12x = 2512
or, x3 = 2512 × 3 × 100/5 × 5 × 12 × 314
= 8
or, x = 2
∴ r = 10, h = 24, l = 26
∴ CSA of cone = πrl
22/7 × 10 × 13 × 2 = 5720/7
= 817.14 cm2.
Question. A metal pipe is 77 cm long. The inner diameter of a cross-section is 4 cm, the outer diameter being 4.4 cm. Find its :
(i) inner curved surface area
(ii) outer curved surface area
(iii) total surface area. (use π = 22/7)
Ans. Inner radius (r) = 2 cm
outer radius (R) = 2.2 cm
Height (h) = 77 cm
(i) C.S.A. (Inner) = 2πrh
= 2 ×22/7 × 2 × 77
= 968 cm2

(ii) C.S.A. (Outer) = 2πRh
= 2 × 22/7 × 2.2 × 77
= 1064.8 cm2.
(iii) Area of top = π(R + r)(R – r)
= 22/7 × 4.2 × 0.2
= 2.64 cm2
= Area of the bottom
∴ T.S.A. = Inner (C.S.A.) + Outer (C.S.A.) + Area of top + Area of bottom
= 968 + 1064.8 + 2 × 2.64
= 2038.08 cm2.
Question. What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m ? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (Use π = 3.14).
OR
Twenty-seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S’. Find the (i) radius R’ of the new sphere, (ii) ratio of S’ and S.
Ans. Conical tent : height = 8 m
base radius = 6 m

l2 = r2 + h2
l2 = 82 + 62
l = √64 + 36 = 10 m
C.S.A of tent = πrl unit2
C.S.A. of Tent = 3.14 × 6 × 10 m2
= 188.4 m2
Area of Tarpaulin = C.S.A of tent
width × length of tarpaulin = 188.4 m2
3 × length of tarpaulin = 188.4 m2
length of tarpaulin = 188.4/3 = 62.8 m
Extra length required for stitching and wastage of cutting
= 20 cm = 0.20 m
∴ Total length of tarpaulin = 62.8 + 0.2 = 63 m
OR
Volume of 1 solid iron sphere = 4/3πr3
Volume of 27 solid iron spheres = 4/3πr3 × 27
Volume of new sphere = 4/3 × 27πr3
(where R is the radius of sphere)
4/3πR3 = 4/3 × 27πr3
R3 = 27r3
(i) R = 3r unit
(ii) Surface area of new sphere = 4πr2
S’ = 4π × (3r)2
S’ = 4π × 9r2 unit2
Surface area of Sphere = 4πr2
S = 4πr2
S’/S = 4π × 9r2/4πr2 = 9/1
S’ : S = 9 : 1
