MCQ Chapter 2 Relations and Functions Class 11 Mathematics

Please refer to Relations and Functions Sections MCQ Questions Class 11 Mathematics below. These MCQ questions for Class 11 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Relations and Functions will help you to prepare for the exams and get more marks.

Relations and Functions MCQ Questions Class 11 Mathematics

Please see solved MCQ Questions for Relations and Functions in Class 11 Mathematics. All questions and answers have been prepared by expert faculty of standard 11 based on the latest examination guidelines.

MCQ Questions Class 11 Mathematics Relations and Functions

Question. If A × B = { (5, 5), (5, 6), (5, 7), (8, 6), (8, 7), (8, 5)}, then the value A is
(a) {5}
(b) {8}
(c) {5, 8}
(d) {5, 6, 7, 8} 

Question. If f : R → R is defined by f(x) = 3x + |x|, then f(2x) – f (– x) – 6x =
(a) f(x)
(b) 2f(x)
(c) – f(x)
(d) f(– x) 

Question. Let A = {x, y, z} and B = {a, b, c, d}. Then, which one of the following is not a relation from A to B?
(a) {(x, a), (x, c)}
(b) {(y, c), (y, d)}
(c) {(z, a), (z, d)}
(d) {(z, b), (y, b), (a, d)} 

Question. The domain of the function f(x) = x² + 3x + 5 / x² – 5x + 4 is
(a) R
(b) R – {1, 4}
(c) R – {1}
(d) (1, 4) 

Question. Let set X = {a, b, c} and Y = Φ. The number of ordered pairs in X × Y are
(a) 0
(b) 1
(c) 2
(d) 3 

Question. Let f(x) = 2x + 5 and g(x) = x² + x. Then, match the functions given in column-I with the expressions in column-II.  

Codes:
     A B C D
(a) 2 4 1 3
(b) 4 1 2 3
(c) 2 1 4 3
(d) 1 4 2 3 

Question. There are three relations R1, R2 and R3 such that
R₁ = {(2, 1), (3, 1), (4, 2)},
R₂ = {(2, 2), (2, 4), (3, 3), (4, 4)} and
R₃ = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7)}
Then,
(a) R₁ and R₂ are functions
(b) R₂ and R₃ are functions
(c) R₁ and R₃ are functions
(d) Only R₁ is a function 

Question. Let X = {1, 2, 3}. The total number of distinct relations that can be defined over X is 2n. The value of ‘n’ is
(a) 9
(b) 6
(c) 8
(d) 2 

Question. Let N be the set of natural numbers and the relation R be defined such that {R = (x, y) : y = 2x, x, y ∈ N}. Then,
(a) R is a function
(b) R is not a function
(c) domain, range and co-domain is N
(d) None of the above 

Question. The relation R defined on the set of natural numbers as {(a, b) : a differs from b by 3}is given
(a) {(1, 4), (2, 5), (3, 6),…..}
(b) {(4, 1), (5, 2), (6, 3),…..}
(c) {(1, 3), (2, 6), (3, 9),…..}
(d) None of these 

Question. Let n(A) = m, and n(B) = n. Then the total number of nonempty relations that can be defined from A to B is
(a) mⁿ
(b) n^m – 1
(c) mn – 1
(d) 2^mn – 1 

Question. The domain of f (x) = 1/√2x–1–√1–x² is:
(a) 1/2 ,1
(b) [ – 1, ∞]
(c) [1, ∞]
(d) None of these 

Question. Let R be the relation on Z defined by
R = {(a, b) : a, b ∈ Z, a – b is an integer}. Then
(a) domain of R is {2, 3, 4, 5, …..}
(b) range of R is Z
(c) Both (a) and (b)
(d) None of the above 

Question. Match the following in column-I with the sets of ordered pairs in column-II. 

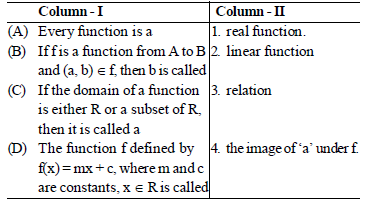
Codes:
     A B C D
(a) 2 4 1 3
(b) 3 4 1 2
(c) 3 1 4 2
(d) 2 1 4 3 

Question. The relation R defined on the set A = {1, 2, 3, 4, 5} by
R = {(x, y) : |x² – y²| < 16} is given by
(a) {(1, 1), (2, 1), (3, 1), (4, 1), (2, 3)}
(b) {(2, 2), (3, 2), (4, 2), (2, 4)}
(c) {(3, 3), (4, 3), (5, 4), (3, 4)}
(d) None of these 

Question. Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Then,
(a) f is a relation from A to B
(b) f is a function from A to B
(c) Both (a) and (b)
(d) None of these 

Question. The domain and range of the real function f defined by f(x) = |x – 1| is
(a) R, [0, ∞)
(b) R, (–∞, 0)
(c) R, R
(d) (–∞, 0), R 

Question. Suppose that the number of elements in set A is p, the number of elements in set B is q and the  number of elements in A × B is 7. Then p² + q² =
(a) 42
(b) 49
(c) 50
(d) 51 

Question. If f (x) = x and g (x) = |x|, then (f + g) (x) is equal to
(a) 0 for all x ∈ R
(b) 2x for all x ∈ R
(c) {2x, for x ≥ 0
     {0, for x < 0
(d) {0, for x ≥ 0
     {2x,for x < 0 

Question. If Φ(x) = a^x, then [Φ(p)]³ is equal to
(a) Φ (3p)
(b) 3Φ (p)
(c) 6Φ (p)
(d) 2Φ (p) 

Question. If  f (x) = x³ – 1/x³  , then f (x) + f (1/x) is equal to
(a) 2 x³
(b) 2.1/x³
(c) 0
(d) 1 

Question. If n (X) = 5 and n (Y) = 7, then the number of relations on X x Y is 25m. The value of ‘m’ is
(a) 5
(b) 7
(c) 6
(d) 8 

Question. Which of the following relation is a function ?
(a) {(a, b) (b, e) (c, e) (b, x)}
(b) {(a, d) (a, m) (b, e) (a, b)}
(c) {(a, d) (b, e) (c, d) (e, x)}
(d) {(a, d) (b, m) (b, y) (d, x)} 

Question. If A = {a, b}, B = {c, d}, C = {d, e}, then {(a, c), (a, d), (a, e), (b, c), (b, d), (b, e)} is equal to
(a) A ∩ (B ∪ C)
(b) A ∪ (B ∩ C)
(c) A × (B ∪ C)
(d) A × (B ∩ C) 

Question. The domain of the function f(x) = 1/√9 – x² is
(a) –3 ≤ x ≤ 3
(b) –3 < x < 3
(c) –9 ≤ x ≤ 9
(d) –9 < x < 9 

Question. If f(y) = 2y²  + by + c and f(0) = 3 and f(2) = 1, then the value of f(1) is
(a) 0
(b) 1
(c) 2
(d) 3 

Question. A relation R is defined in the set Z of integers as follows (x, y) ∈ R iff x² + y² = 9. Which of the following is false?
(a) R = {(0, 3), (0, –3), (3, 0), (–3, 0)}
(b) Domain of R = {–3, 0, 3}
(c) Range of R = {–3, 0, 3}
(d) None of these 

Question. If f(x) = 2^x + 2^–x / 2 , then f(x + y). f(x – y) =
(a) 1/2 [f(2x) + f (2y)]
(b) 1/4 [f (2x) f (2y)]
(c) 1/2[f (2x) – f (2y)]
(d) 1/4[f (2x) – f (2y)] 

Question. The domain and range of the function f given by f(x) = 2 – |x – 5| is
(a) Domain = R⁺, Range = (–∞, 1]
(b) Domain = R, Range = (–∞, 2]
(c) Domain = R, Range = (–∞, 2)
(d) Domain = R⁺, Range = (–∞, 2] 

Question. Let A = {1, 2, 3, 4, ….., 14}. A relation R from A to A is defined by R = {(x, y) : 3x – y = 0, where x, y ∈ A}. 

Codes:
     A B C D
(a) 4 3 2 1
(b) 4 1 2 3
(c) 4 2 1 3
(d) 4 3 1 2 

Question. Let f(x) = 1 + x, g(x) = x² + x + 1, then (f + g) (x) at x = 0 is
(a) 2
(b) 5
(c) 6
(d) 9 

Question. The domain and range of the relation R given by
R = {(x, y) : y = x + 6/x ; where x, y ∈ N and x < 6} is
(a) {1, 2, 3}, {7, 5}
(b) {1, 2}, {7, 5}
(c) {2, 3}, {5}
(d) None of these 

Question. The cartesian product of A × A has 9 elements, two of which are (–1, 0) and (0, 1), the remaining elements of A × A is given by
(a) {(–1, 1), (0, 0), (–1, –1), (1, –1), (0, –1)}
(b) {(–1, –1), (0, 0), (–1, 1), (1, –1), (1, 0), (1, 1), (0, –1)}
(c) {(1, 0), (0, –1), (0, 0), (–1, –1), (1, –1), (1, 1)}
(d) None of these 

Question. If f (x) = 1– x/1+ x , then f (1– x/1+ x) is equal to:
(a) x
(b) 1– x/1+ x
(c) 1+ x/1– x
(d) 1/x 

STATEMENT TYPE QUESTIONS 

Question. Consider the following statements.
I. If the set A has 3 elements and set B = {3, 4, 5}, then the number of elements in A x B = 9.
II. The domain of the relation R defined by 
R = {(x, x + 5) : x ∈ (0, 1, 2, 3, 4, 5)} is {5, 6, 7, 8, 9, 10}.
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both I and II are true.
(d) Both I and II are false. 

Question. Which of the following is/are true?
I. If P = {m, n} and Q = {n, m}, then P × Q = {(m, n), (n, m)}.
II. If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y), such that
x ∈ A and y ∈ B.
III. If A = {1, 2} and B = {3, 4}, then A × (B∩Φ) = Φ.
(a) I and II are true
(b) II and III are true
(c) I and III are true
(d) All are true  

Question. Consider the following statements.
I. If X = {p, q, r, s} and Y = {1,2, 3, 4, 5}, then {(p, 1), (q, 1), (r, 3), (s, 4)} is a function.
II. Let A = {1, 2, 3, 4, 6}. If R is the relation on A defined by {(a, b) : a, b ∈ A, b is exactly divisible by a}.
The relation R in Roster form is {(6, 3), (6, 2), (4, 2)}
Choose the correct option.
(a) Only I is false.
(b) Only II is false.
(c) Both I and II are false.
(d) Neither I nor II is false. 

Question. Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b²}. Then, which of the following is/are true? 
I. (a, a) ∈ R for all a ∈ N.
II. (a, b) ∈ R implies (b, a) ∈ R.
III. (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
(a) I and II are true
(b) II and III are true
(c) All are true
(d) None of these 

Question. Consider the following statements.
I. The relation R = {(x, x³) : x is a prime number less than 10 } in Roster form is {(3, 27), (5, 125), (7, 343)}
II. The range of the relation
R = {(x + 2, x + 4) : x ∈ N, x < 8} is {1, 2, 3, 4, 5, 6, 7}.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false 

Question. Consider the following statements.
I. Let f = {(1, 1), (2, 3), (0, –1), (–1, –3)} be a linear function from Z to Z. Then, f(x) is 2x –1.
II. If f(x) = x³ – 1/x³ , then f(x) + f(1/x) is equal to 0.
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both are true.
(d) Both are false. 

Question. Consider the following statements.
Let A = {1, 2, 3, 4} and B = {5, 7, 9}
I. A x B = B x A
II. n (A x B) = n (B x A)
Choose the correct option.
(a) Statement-I is true.
(b) Statement-II is true.
(c) Both are true.
(d) Both are false. 

Question. Consider the following statements :
I. If n (A) = p and n (B) = q, then n (A × B) = pq
II. A × Φ = Φ
III. In general, A × B ≠ B × A
Which of the above statements are true ?
(a) Only I
(b) Only II
(c) Only III
(d) All of the above