Please refer to Inverse Trigonometric Functions MCQ Questions Class 12 Mathematics below. These MCQ questions for Class 12 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Inverse Trigonometric Functions will help you to prepare for the exams and get more marks.
Inverse Trigonometric Functions MCQ Questions Class 12 Mathematics
Please see solved MCQ Questions for Inverse Trigonometric Functions in Class 12 Mathematics. All questions and answers have been prepared by expert faculty of standard 12 based on the latest examination guidelines.
MCQ Questions Class 12 Mathematics Inverse Trigonometric Functions
Question. If xy + yz + zx = 1, then :
(a) tan–1 x +tan–1 y + tan–1 z = 0
(b) tan–1 x + tan–1 y +tan–1 z = π
(c) tan–1 x +tan–1 y +tan–1 z = π/4
(d) tan–1 x + tan–1 y + tan–1 z = π/2
Answer
D
Question. If sin (cot–1(1 +x)) = cos (tan–1x), then x =
(a) 1/2
(b) 1
(c) 0
(d)−1/2
Answer
D
Question. If sin –1 (6x/1+9x2) = 2tan –1(ax), then a =
(a) 3
(b) 8
(c) 6
(d) 9
Answer
A
Question. cot–1(ab + 1/a − b) + cot–1(bc + 1/b − c) + cot–1(ca + 1/c − a) is equal to …
(a) 0
(b) π/4
(c) 1
(d) 5
Answer
A
Question. If tan–13 + tan–1 x = tan–18, then x =
(a) 5
(b) 1/5
(c) 5/14
(d) 14/5
Answer
B
Question. Which of the following is the principal value branch of cosec–1x?
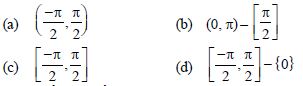
Answer
D
Question. If sin–1(1– x ) – 2 sin–1 x = π/2 ,then x equals
(a) 0,−1/2
(b) 0, 1/2
(c) 0
(d) None of these
Answer
B
Question. Principal value of sec–1(2) is equal to
(a) π/6
(b) π/3
(c) 2π/3
(d) 5π/3
Answer
B
Question.

then the value of A–B is
(a) 10°
(b) 45°
(c) 60°
(d) 30°
Answer
D
Question. The value of cos–1 (cos3π/2) is equal to
(a) π/6
(b) 3π/2
(c) 5π/2
(d) 7π/2
Answer
A
Question. If sin(sin–11/5 + cos–1x 1) = 1, then the value of x is
(a) –1
(b) 2/5
(c) 1/3
(d) 1/5
Answer
D
Question. If cos–1x + cos–1y + cos–1z = 3π then xy + yz + zx is equal to :
(a) 1
(b) 0
(c) –3
(d) 3
Answer
D
Question. If sin–1(1/5) + sec–1(2) + 2tan–1(1/√3) + sec–1(5) + sin–1(1/2) + 2tan–1(√3) = kπ, then k =
(a) 1
(b) 2
(c) 4
(d) 5
Answer
B
Question. The value of tan–1(1/2) + tan–1(1/3) + tan–1(7/8) is
(a) tan–1(7/8)
(b) cot–1 (15)
(c) tan–1(15)
(d) tan–1(25/24)
Answer
C
Question. cos–1(1/2) + sin–1(1/2) + tan–11/√3 is equal to
(a) π
(b) π/3
(c) 4π/3
(d) 3π//4
Answer
A
Question. The value of tan (cos–14/5 + tan–12/3) =
(a) 6/17
(b) 7/16
(c) 16/7
(d) None of these
Answer
D
Question. The value of expression 2sec–1 2+ sin–1(1/2) is
(a) π/6
(b) 5π/6
(c) 7π/6
(d) 1
Answer
B
Question. If |x| ≤ 1, then 2 tan–1x + sin–1 (2x/1+ x2) is equal to
(a) 4 tan–1x
(b) π/2
(c) 0
(d) π
Answer
A
Question. Domain of cos–1[x] is
(a) [–1, 2]
(b) [–1, 2)
(c) (–1, 2]
(d) None of these
Answer
B
Question. sin {2cos–1 (–3/5)} is equal to
(a) 6/25
(b) 24/25
(c) 4/5
(d) – 24/25
Answer
D
Question. If tan−1(x +1) + cot−1(x −1) = sin−1 4/5 + cos−1 3/5 then x has the value :
(a) 4√3/7
(b) 4√7/3
(c) 14√3
(d) 6√7
Answer
A
Question. If cos–1 (1/√5) = θ , then the value of cosec–1 (√5) is
(a) (π/2) + θ
(b) (π/2) − θ
(c) π/2
(d) − θ
Answer
B
Question.
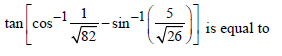
(a) 2/23
(b) 4/31
(c) 29/3
(d) 6/13
Answer
A
Question. The value of cos–1(cos5π/3) + sin–1(sin5π/3) is
(a) π/2
(b) 5π/3
(c) 10π/3
(d) 0
Answer
D
ASSERTION- REASON TYPE QUESTIONS
(a) Assertion is correct, reason is correct; reason is a correctexplanation for assertion.
(b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, reason is incorrect
(d) Assertion is incorrect, reason is correct.
Question. Assertion: If x < 0, tan–1 x + tan –1 (1/x) = π/2
Reason: tan–1x + cot –1 x = π/2, ∀ x ∈ R
Answer
D
Question. Assertion: 2tan–11/2 + tan–11/7 = tan–1 31/17.
Reason: 2tan–1x = tan–1 (2x/1 − x2) if –1 < x < 1.
Answer
A
Question. Assertion: cosec–1(3/2) + cos–1(2/3) − 2cot–1(1/7) − cot–1(7) is equal to cot–17.
Reason: sin–1x + cos–1x = π/2 , tan–1 x + cot–1 x = π/2
cosec–1x = sin–1(1/x), cot–1(x) = tan–1(1/x)
Answer
D
Question. Assertion: To define the inverse of the function f (x) = tan x any of the intervals
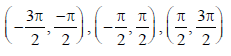
etc. can be chosen.
Reason: The branch having range , (−π/2, π/2) is called principal value branch of the function g(x) = tan–1x.
Answer
B
Question. Assertion : The value of tan–1(3/4) + tan–1(1/7) is π/4
Reason : If x > 0, y > 0 then tan–1(x/y) + tan–1(y − x/y + x) = π/4
Answer
A
Question. Assertion: sin–1 8/17 + sin–1 3/5 = sin–1 77/85
Reason: tan–1x + tan–1y = tan–1(x + y/1 − xy)
Answer
B


