Please refer to Application of Derivatives MCQ Questions Class 12 Mathematics below. These MCQ questions for Class 12 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Application of Derivatives will help you to prepare for the exams and get more marks.
Application of Derivatives MCQ Questions Class 12 Mathematics
Please see solved MCQ Questions for Application of Derivatives in Class 12 Mathematics. All questions and answers have been prepared by expert faculty of standard 12 based on the latest examination guidelines.
MCQ Questions Class 12 Mathematics Application of Derivatives
Question. The function f(x) = cot–1x + x increases in the interval
(a) (1, ∞)
(b) (– 1, ∞)
(c) (0, ∞)
(d) (– ∞, ∞)
Answer
D
Question. The function f (x) log (cos x ) is strictly decreasing and strictly increasing in
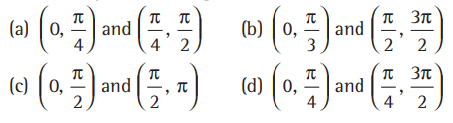
Answer
C
Question. The value of x for which the polynomial 2×3-9×2+ 12x +4 is a decreasing function of x, is
(a) −1 <x < 1
(b) 0 <x <2
(c) x > 3
(d) 1 <x <2
Answer
D
Question. If f (x) = 1/x+1- log(1+x),x> 0, then f is
(a) an increasing function
(b) a decreasing function
(c) both increasing and decreasing function
(d) None of the above
Answer
B
Question. The function which is neither decreasing nor increasing in (π/2, 3π/2), is
(a) cosec x
(b) tan x
(c) x2
(d)|x−1|
Answer
A
Question.

Answer
D
Question. Among sin (tan2 ), sin (tan 5/2),sin (tan 3) and sin (tan 4), which one is smallest?
(a) sin (tan )2
(b) sin (tan 5/2)
(c) sin (tan 3)
(d) sin (tan 4)
Answer
C
Question. Which of the following is biggest?
(a) cos 1
(b) cos 2
(c) cos 3
(d) cos 4
Answer
A
Question. The function f (x)=x1/x is
(a) increasing in (1 ,∞)
(b) decreasing in (1,∞)
(c) increasing in ( 1, e) and decreasing in (e,∞)
(d) decreasing in (1, e) and increasing in (e ,∞)
Answer
C
Question. The function f (x) = tan x – 4x is strictly decreasing on
(a) (−π/4,π/4)
(b) (−π/6,π/6)
(c) (−π/3,π/3)
(d) (−π/2,π/2)
Answer
C
Question. If f (x)= xα log x and f (0) =0, then the value of α for which Rolle’s theorem can be applied in [0, 1], is
(a) −2
(b) −1
(c) 0
(d) 1/2
Answer
D
Question.
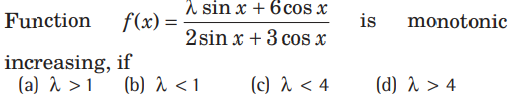
Answer
D
Question.
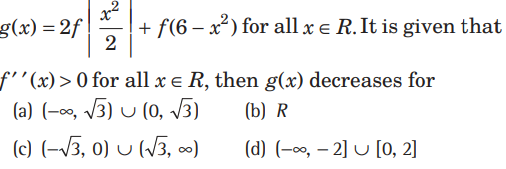
Answer
D
Question.

(a) a = −11
(b) a = −6
(c) a = 6
(d) a = 11
Answer
D
Question.
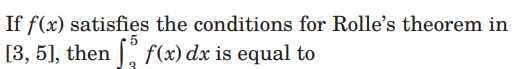
(a) 2
(b) −1
(c) 0
(d) −4/3
Answer
D
Question.

Answer
C
Question.

(a) 3
(b) 0
(c) 1
(d) 2
Answer
B
Question. Suppose the cubic equation x3-px+ q= 0 has three distinct real roots, where p> 0 and q > 0.Then, which one of the following holds?
(a) The cubic has minima at both √p/3 and -√p/3
(b) The cubic has maxima at both √p/3 and -√p/3
(c) The cubic has minima at √p/3 and maxima at −√p/3
(d) The cubic has minima at -√p/3 and maxima at√p/3
Answer
C
Question. Line joining the points (0,3) and (5,2) is a tangent to the curve y=ax/1+x ,then
(a) a = ± 1 √3
(b) a = φ
(c) a = − ± 1√3
(d) a = − ± 2√3
Answer
B
Question.
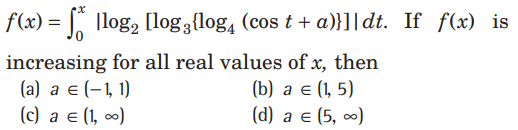
Answer
D
Question. y= f(x) = is a parabola, having its axis parallel to y-axis. If the line y= x touches this parabola at x = 1,then
(a) f'(1) + f'(0)=1
(b) f'(0) – f'(0)=1
(c) f′ (1)-f'(0)=1
(d) f′(0) + f'(1)=1
Answer
A
Question. The parabolas y2=4ax = and x2= 4by intersect orthogonally at point P (x1,y1), where x1,y1 ≠ 0, then
(a) b =a2
(b) b =a3
(c) b3= a2
(d) None of the
Answer
B
Question. The slope of tangent to the curve x= t2+3t-8, y=2t2-2t-5 at the point(2,-1) is
(a) (a) 22/ 7
(b) 6/ 7
(c) –6
(d) None of these
Answer
B
Question.
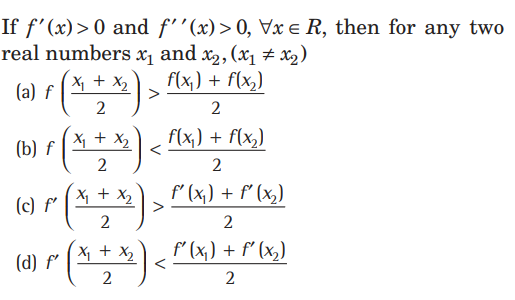
Answer
B
Question. If f (x) =x/ sin x and g(x) =x/ tan x’ where 0<x ≤1, then in this interval
(a) both f(x) and g (x) are increasing functions
(b) both f (x) and g (x) are decreasing
(c) f (x) is an increasing function
(d) g (x) is an increasing function
Answer
C
Question.

Answer
B
Question. The curve y = x1/5 at (0, 0) has
(a) a vertical tangent (parallel to y-axis)
(b) a horizontal tangent (parallel to x-axis)
(c) no oblique tangent
(d) no tangent
Answer
B
Question. A window is in the form of rectangle surmounted by a semi-circular opening. The total perimeter of the window is 10 m.
Statement I: One of the dimension of the window to admit maximum light through the whole opening is 20/π + 4 m.
Statement II: One of the dimension of the window to admit maximum light through the whole opening is 10/π + 4 m.
(a) Only statement I is true
(b) Only statement II is true
(c) Both the statements are true
(d) None of the above
Answer
C
Question. A kite is moving horizontally at a height of 151.5. If the speed of kite is 10 m/s, then the rate at which the string is being let out; when the kite is 250 m away from the boy who is flying the kite and the height of the boy is 1.5 m, is
(a) 4 m/s
(b) 6 m/s
(c) 7 m/s
(d) 8 m/s
Answer
D
Question. Water is dripping out from a conical funnel of semi-vertical angle π/ 4 at the uniform rate of 2 cm2/s is the surface area through a tiny hole at the vertex of the bottom. When the slant height of cone is 4 cm, then rate of decrease of the slant height of water is
(a)√2/3π cm/s
(b) √2/π cm/s
(c) √2/4π cm/s
(d) None of these
Answer
C
Question. If f(x) = cosx, g(x) = cos 2x, h(x) = cos3x and I(x) = tanx, then which of the following option is correct?
(a) f(x) and g(x) are strictly decreasing in (0, π/2)
(b) h(x) is neither increasing nor decreasing in (0, π/2)
(c) I(x) is strictly increasing in (0, π/2)
(d) All are correct
Answer
D
Question. The equation of one of the tangents to the curve y = cos(x +y), -2π ≤ x ≤ 2π that is parallel to the line x + 2y = 0, is
(a) x + 2y = 1
(b) x + 2y = π/2
(c) x + 2y = π/4
(d) None of these
Answer
B
Question. If the parabola y = f (x), having axis parallel to the y-axis, touches the line y = x at (1, 1), then
(a) 2 f ‘(0) + f (0) = 1
(b) 2 f (0) + f ‘(0) = 1
(c) 2 f (0) – f ‘(0) = 1
(d) 2 f ‘(0) – f (0) = 1
Answer
B
Question. Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45° to each other.
Statement I: If they travel by different roads, then the rate at which they are being separated, is (√2-√2) v unit / s .
Statement II: If they travel by different roads, then the rate at which they are being separated, is 2v sin π/8 unit/s.
(a) Only statement I is true
(b) Only statement II is true
(c) Both the statements are true
(d) Both the statements are false
Answer
C
Question. The maximum value of the function y = – x2 in the interval [–1, 1] is
(a) 0
(b) 2
(c) 8
(d) 9
Answer
A
Question. The largest distance of the point (a, 0) from the curve 2x2 + y2 – 2x = 0, is given by

Answer
D
Question. Let AP and BQ be two vertical poles at points A and B respectively. If AP = 16 m, BQ = 22 m and AB = 20 m, then the distance of a point R on AB from the point A such that RP2 + RQ2 is minimum, is
(a) 5 m
(b) 6 m
(c) 10 m
(d) 14 m
Answer
C
Question. The maximum value of [x(x – 1) + 1]1/3, 0 ≤ x ≤ 1 is
(a) (1/3)1/3
(b) 1/2
(c) 1
(d) zero
Answer
C
Question. The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm/s. If the two equal sides are equal to the base then the rate at which its area is decreasing, is
(a) b/3 cm2 / s
(b) b2 cm2/s
(c) b/√3 cm2 / s
(d) b √3cm2 / s
Answer
D
Question. A football is inflated by pumping air in it. When it acquires spherical shape its radius increases at the rate of 0.02 cm/s. The rate of increase of its volume when the radius is 10 cm is ___________ π cm/s
(a) 0
(b) 2
(c) 8
(d) 9
Answer
C
Question. If the radius of a spherical balloon increases by 0.2%. Find the percentage increase in its volume
(a) 0.8%
(b) 0.12%
(c) 0.6%
(d) 0.3%
Answer
C
Question. The function f(x) = x2 log x in the interval [1, e] has
(a) a point of maximum and minimum
(b) a point of maximum only
(c) no point of maximum and minimum in [1, e]
(d) no point of maximum and minimum
Answer
C
Question. The equation of all lines having slope 2 which are tangent to the curve y = 1/x-3 , x ≠ 3 , is
(a) y = 2
(b) y = 2x
(c) y = 2x + 3
(d) None of these
Answer
D
Question. If f be a function defined on an open interval I. Suppose c ∈ I be any point. If f has a local maxima or a local minima at x = c, then
Statement I: f'(c) = 0
Statement II: f is not differentiable at c.
(a) Only statement I is true
(b) Only statement II is true
(c) Both the statements I and II are true
(d) Both the statements I or II are false
Answer
D
Question. Each side of an equilateral triangle expands at the rate of 2 cm/s. What is the rate of increase of area of the triangle when each side is 10 cm?
(a) 10 √2 cm2 / s
(b) 10 √3 cm2 /s
(c) 10 cm2/s
(d) 5 √3 cm2 /s
Answer
B
Question. If the curves x2 = 9A (9 – y) and x2 = A(y + 1) intersect orthogonally, then the value of A is
(a) 3
(b) 4
(c) 5
(d) 7
Answer
B
Question. The equation of the tangent to 4x2 – 9y2 = 36 which is perpendicular to the straight line 5x + 2y – 10 = 0 is
(a) 5(y – 3) = 4 (x -√11/2)
(b) 2x -5y +10 -12 √3 = 0
(c) 2x -5y +10 +12 √3 = 0
(d) None of these
Answer
D
Question. If the error k% is made in measuring the radius of a sphere, then percentage error in its volume is
(a) k%
(b) 3k%
(c) 2k%
(d) k/3 %
Answer
B
Question. If the radius of a sphere is measured as 9 cm with an error of 0.03 cm, then find the approximating error in calculating its volume.
(a) 2.46π cm3
(b) 8.62π cm3
(c) 9.72π cm3
(d) 7.6π cm3
Answer
C
Question. Find the maximum profit that a company can make, if the profit function is given by P(x) = 41 + 24x – 18x2.
(a) 25
(b) 43
(c) 62
(d) 49
Answer
D
Question. An isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a.
Statement I: The area of triangle is maximum when θ = π/6
Statement II: The area of triangle is minimum when θ = π/6
(a) Only statement I is true
(b) Only statement II is true
(c) Both the statements are true
(d) Both the statements are false
Answer
A
Question. If a point on the hypotenuse of a triangle is at distance a and b from the sides of triangle, then the minimum length of the hypotenuse is
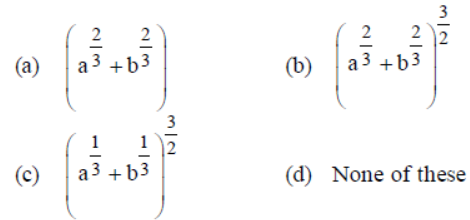
Answer
B
A cubic f (x) ax =ax3+bx2 + cx +d

On the basis of above information, answer the following questions.
Question. The function f (x ) is
(a) x3+ x2+x-2
(b) x3 – x2 + x-2
(c) x3 – x2– x+2
(d) x3 + x2 – x+2
Answer
D
Question. The value of d is
(a) 5
(b) 2
(c) 0
(d) − 4
Answer
B
Question. The nature of roots of f (x) = 3 is
(a) one root is real and other two are distinct
(b) all roots real and distinct
(c) all roots are real; two of them are equal
(d) None of the above
Answer
C
Question. f (x) decreases in the interval50
(a) (−1/3,1)
(b) (-1/3,-1)
(c) (−1,1/3)
(d) (1,3/2)
Answer
C
Question. The value of c is
(a) −2
(b) −1
(c) 0
(d) 2
Answer
B
Each of these questions contains two statements : Statement I (Assertion) and Statement II (Reason). Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c) and (d) given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true.
Question. Consider the ordinate of a point describing the circle x2+ y2= 25 decreases at the rate of 1.5 cm/s.
Statement I Then the rate of change of the abscissa of the point when ordinate equals to 4 cm in 2 cm/s.
Statement II x dx +y dy = 0
Answer
A
Question. Statement I If Rolle’s theorem be applied in f (x),then Lagrange Mean Value Theorem (LMVT) is also applied in f (x).
Statement II Both Rolle’s theorem and LMVT cannot be applied in f (x) =|sin| || = in [− π/4,π/4].
Answer
B
Question. Statement I Shortest distance between |x |+|y| = 2 and x2+y2=16 is 4-√2.
Statement II Shortest distance between the two smooth curves lies along the common normal
Answer
A
Question. Statement I Let f :R → R be a function such that f (x)=x3+x2+3x+ sin x. Then, f is one one.
Statement II f (x) is decreasing function.
Answer
C
Question. If g (x) is a differentiable function g(1)≠0, g(-1 )≠ 0 and Rolle’s theorem is not applicable to f(x)=x2-1/g(x) in [ -1,1], then
Statement I g (x) has at least one root in (−1 ,1).
Statement II If f (a)= f (b). Rolle’s theorem is applicable for x ∈( a,b ).
Answer
C
Question. Statement I A tangent parallel to x-axis can be drawn for f (x)=(x-1)(x-2) (x-3) in the interval [1, 3].
Statement II A horizontal tangent can be drawn in Rolle’s theorem.
Answer
B
Question. Statement I If f (x)=x(x+3)e-x/2, then Rolle’s theorem applies for f(x) in [-3,0].
Statement II Lagrange mean value theorem is applied in f(x)=x(x+3)e-x/2, in any interval.
Answer
B
Question. Statement I If f (x) is continuous in [a ,b] and differentiable in (a ,b ) then there exists at least one
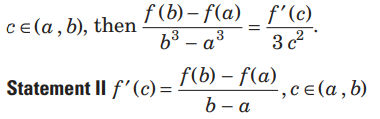
Answer
B
Question. Consider the equation x 3- 3x +k =0, k∈ R.
Statement I There is no value of k for which the given equation has two distinct roots in (0,1)
Statement II Between two consecutive roots of f ‘(x) = 0, {f(x) is a polynomial}, f(x) = 0 must have one root.
Answer
C
Matching Type Questions :
| Column-I | Column-II |
| A. f(x) = x2 – 2x + 5 is | strictly decreasing in (– ∞, –1) and strictly increasing in (– 1, – ∞). |
| B. f(x) = 10 – 6x – 2x2 is | strictly increasing in (–∞, –9/2) and strictly decreasing in (-9/2 , ∞). |
| C. f(x) = – 2x3 – 9x2 – 12x + 1 is | strictly decreasing in (– ∞, –2) and (– 1, ∞) and strictly increasing in (– 2, – 1) |
| D. f (x) = 6 – 9x – x2 is | strictly increasing in (–∞, –9/2) and strictly decreasing in (-3/2 , ) |
| E. (x + 1)3 (x – 3)3 is | strictly increasing in (1, 3) and (3, ∞) and strictly decreasing in (– ∞, –1) and (– 1, 1) |
Codes
A B C D E
(a) 1 2 3 4 5
(b) 2 3 4 1 5
(c) 1 4 3 2 5
(d) 5 4 3 2 1
Answer
C
Question.
| Column-I (Function) | Column-II (Maximum and minimum values respectively) |
| A. f(x) = |x + 2| – 1 has | no maximum value and – 1 as minimum value |
| B. g(x) = – |x + 1| + 3 has | 3 as maximum value, but it has no minimum value |
| C. h(x) = sin(2x) + 5 has | 6 as maximum value, and 4 as minimum value |
| D. F(x) = |sin4x + 3| has | 4 as maximum value, and 2 as minimum value |
| E. h(x) = x + 1, x ∈ (– 1, 1) has | neither a maximum value nor a minimum value |
Codes
A B C D E
(a) 1 2 3 4 5
(b) 2 3 4 1 5
(c) 1 3 2 4 5
(d) 3 1 2 5 4
Answer
A

