Students should refer to Worksheets Class 12 Mathematics Continuity and Differentiability Chapter 5 provided below with important questions and answers. These important questions with solutions for Chapter 5 Continuity and Differentiability have been prepared by expert teachers for Class 12 Mathematics based on the expected pattern of questions in the class 12 exams. We have provided Worksheets for Class 12 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Continuity and Differentiability Worksheets Class 12 Mathematics
Question. If f (x) = x2 sin1/x, where x ≠ 0, then the value of the function f at x = 0, so that the function is continuous at x = 0, is
(a) 0
(b) – 1
(c) 1
(d) None of these
Answer
A
Question. If sin y + e–x cos y = e , then dy/dx at (1, π) is equal to
(a) sin y
(b) – x cos y
(c) e
(d) sin y – x cos y
Answer
C
Question. If 2x + 2y = 2x + y, then dy/dx =
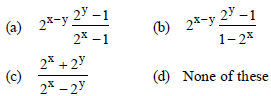
Answer
D
Question.
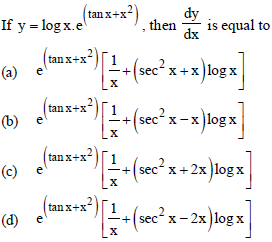
Answer
C
Question. Let 3f(x) – 2f(1/x) = x, then f ‘(2) is equal to
(a) 2/7
(b) 1/2
(c) 2
(d) 7/2
Answer
B
Question. Match the functions given in column – I with their derivatives in column – II.
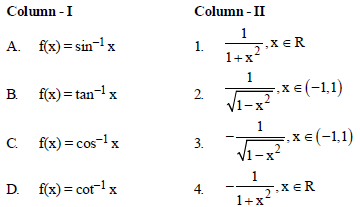
Codes
A B C D
(a) 3 1 2 4
(b) 2 1 3 4
(c) 1 4 3 2
(d) 1 2 3 4
Answer
B
Question. Let f (x) = 1 – tan x/4x – π , x ≠ π/4 , x ∈ (0,π/2). If f(x) is continuous in (0,π/2) , then f(π/4) =
(a) 1
(b) 1/2
(c) –1/2
(d) – 1
Answer
C
Question.

Answer
B
Question. The differential equation satisfied by the function
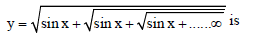
(a) (2y –1)dy/dx – sin x = 0
(b) (2y–1)cosx +dy/dx = 0
(c) (2y–1)cosx – dy/dx = 0
(d) (2y–1)dy/dx – cosx = 0
Answer
D
Question. If x = f(t) and y = g(t), then d2y/dx2 is equal to
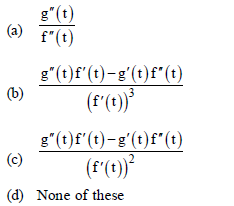
Answer
B
Question. If y = x – x2 , then the derivative of y2 with respect to x2 is
(a) 1– 2x
(b) 2 – 4x
(c) 3x – 2x2
(d) 1– 3x + 2x2
Answer
A
Question. If y = log (1–x2/1+x2), then dy/dx , is equal to
(a) 4x3/1– x4
(b) –4x/1– x4
(c) 1/4 – x4
(d) –4x3/1– x4
Answer
B
ASSERTION – REASON TYPE QUESTIONS
(a) Assertion is correct, reason is correct; reason is a correct explanation for assertion.
(b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, reason is incorrect
(d) Assertion is incorrect, reason is correct.
Question. Assertion : The function defined by f(x) = cos(x2) is a continuous function.
Reason : The cosine function is continuous in its domain i.e., x ∈ R.
Answer
B
Question. Assertion : f (x) = | [x] x | in x ∈ [–1, 2], where [ . ] represents greatest integer function, is non-differentiable at x = 2.
Reason : Discontinuous function is always non differentiable.
Answer
A
Question. Assertion : If x = at2 and y = 2at, then d2y/dx2|t=2 = –1/6a
Reason : d2y/dx2 = (dy/dt)2 × (dt/dx)2
Answer
C
Question. Assertion : f (x) = | x | sin x, is differentiable at x = 0.
Reason : If f (x) is not differentiable and g (x) is differentiable at x = a, then f (x) . g (x) can still be differentiable at x = a.
Answer
A
Question. Assertion : Rolle’s theorem can not be verified for the function f (x) = |x| in the interval [–1, 1].
Reason : The function f (x) = |x| is differentiable in the interval (–1, 1) everywhere.
Answer
C
Question. Assertion : If u = f(tanx), v = g(secx) and f ‘(1) = 2,
g (√2)= 4, then (du/dv)x = π / 4 = 1/√2
Reason : If u = f(x), v = g(x), then the derivative of f with respect to g is du/dv = du/dx / dv/dx
Answer
A
Question. Assertion : The function f (x) = |sin x| is not differentiable at points x = nπ.
Reason : The left hand derivative and right hand derivative of the function f (x) = |sin x| are not equal at points x = nπ.
Answer
D
Question. Assertion : Every differentiable function is continuous but converse is not true.
Reason : Function f(x) = |x| is continuous.
Answer
B