Students should refer to Worksheets Class 12 Mathematics Vector Algebra Chapter 10 provided below with important questions and answers. These important questions with solutions for Chapter 10 Vector Algebra have been prepared by expert teachers for Class 12 Mathematics based on the expected pattern of questions in the class 12 exams. We have provided Worksheets for Class 12 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Vector Algebra Worksheets Class 12 Mathematics
Question. If DA a AB b = = , and CB a =k , wherek > 0and X Y, are the mid-points of DB and AC respectively such that |a| =17 and | XY | =4, then k is
equal to
(a) 8/17
(b) 9/17
(c) 5/17
(d) 4/17
Answer
B
Question. If a and b are two unit vectors inclined to x-axis at angles 30° and 120°, then| | a b + is equal to
(a)√2/3
(b)√2
(c)√3
(d)2
Answer
B
Question.
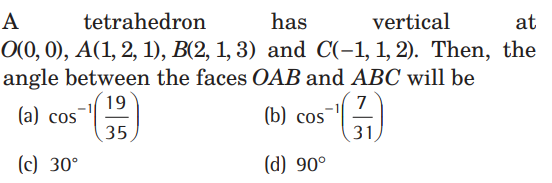
Answer
A
Question. What is the value of (d+a )· [ax {bx (cxd)}] ?
(a) (d· a) ·[b c d]
(b) (a· d) ·[b c d]
(c) (b· d) ·[a c d]
(d) (b· d) ·[a d c]
Answer
C
Question.
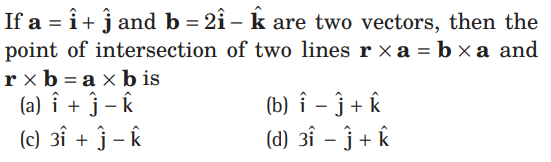
Answer
C
Question.

Answer
B
Question.
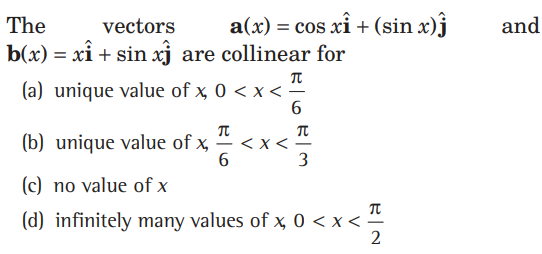
Answer
B
Question.
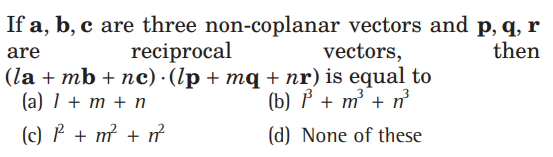
Answer
C
Question.
(a) 60
(b) 68
(c) -60
(d) -74
Answer
D
Question.
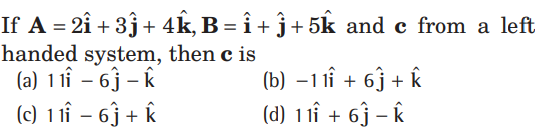
Answer
B
Question.
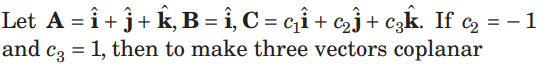
(a) c1 = 0
(b) c1 = 1
(c) c1 = 2
(d) no value of c1 can be found
Answer
D
Question. The sum of two unit vectors is a unit vector. The magnitude of their difference is
(a) 2
(b) √3
(c) √2
(d) 1
Answer
B
Question. For non-zero vector a and b, if |a+b|< |a-b|, then a and b are
(a) collinear
(b) perpendicular to each other
(c) inclined at an acute angle
(d) inclined at an obtuse angle
Answer
D
Question. (ax b)x= ax(b x c) if
(a) (a x b)x c =0
(b) c x a=b
(c) (a x c) x b =0
(d) a·(b x c)
Answer
C
Question. The angle between and b is π/6, then angle between 2a and 3b is
(a) π/3
(b) π/2
(c) π/6
(d) 3π/4
Answer
C
Question. If a and b are two unit vectors such that a b + 2 and 5a- 4b – are perpendicular to each other, then the angle between a and b is
(a) 30°
(b) 60°
(c) cos- 1(3/5)
(d) cos- 1(4/7)
Answer
B
Question.

Answer
D
Question.

(a) √14
(b) 2√51
(c) 3√41
(d) 2√41
Answer
D
Question.
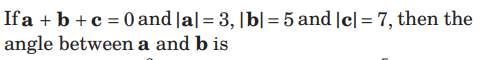
(a) π/6
(b) 2π/3
(c) π/3
(d) 5π/3
Answer
C
Question.

(a) 30°
(b) 45°
(c) 60°
(d) 15°
Answer
C
Question.
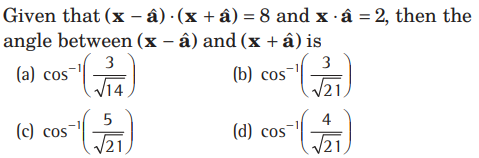
Answer
D
Question. If a and b are unit vectors, then the greatest value of
|a+b |+ |a-b| is
(a) 2
(b) 4
(c) 2√2
(d) √2
Answer
C
Question. If a, b and c are non-coplanar vectors and r is a real number, then the vectors a+2b +3c, λb+4c and
(2λ- 1)c are non-coplanar for
(a) no value ofλ
(b) all except one value of λ
(c) all except two values of λ
(d) all values ofλ
Answer
C
Question. Let u v, and w be three vectors such that |u | =1|v |=2,|w| = 3. If the projection of v along u is equal to that of w along u , v and w are perpendicular to each other, then |u-v+w| is equal to
(a) 4
(b) √7
(c) √14
(d) 2
Answer
C
Question. If V is the volume of the parallelopiped having three coterminus edges, as a, b and c, then the volume of the parallelopiped having three coterminus edges as

Answer
A
Question.
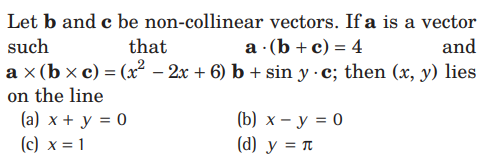
Answer
B
Question.

(a) 1
(b) 2
(c) 3
(d) 4
Answer
C
Question. Vectors a and b are such that |a|=1,| b|=4 and a · b× = 2. If c =2axb- 3b , then the angle between b and c is
(a) π/6
(b) 5/π
(c) π/3
(d) 2π/3
Answer
B
Question.

(a) 10
(b) 8
(c) 2√26
(d) 6
Answer
C
Question.
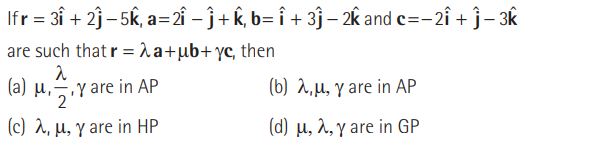
Answer
A
Question. Let ABCD be a parallelogram whose diagonals intersect at P and let O be the origin, then OA+ OB+ OC+ OD equal to
(a) OP
(b) 2OP
(c) 3OP
(d) 4OP
Answer
D
Question. The position vectors of three points are 2a-b+3c,a-2b+λc and µa-5b, where a ,b and c are non-coplanar vectors. The points are collinear, when

Answer
C
Question. If ABCD is a rhombus whose diagonals cut at the origin O, then OA+ OB+ OC+ OD equals
(a) AB+ AC
(b) O
(c) 2(AB +BC)
(d) AC+ BD
Answer
B
Question. A point O is the centre of circle circumscribed about a ΔABC. Then,OA sin2A+0B sin2B+0C sin 2C is equal to
(a) ( OA+OB+OC))sin 2A
(b) 3OG, where Gis centroid of ΔABC
(c) O
(d) None of the above
Answer
C
Question. If a and bare position vectors of A and B respectively and C is a point on AB produced such that AC= 3AB then position vector of C is
(a) 3a -2b
(b) 3b- 2a
(c) 3b+ 2a
(d) 2a-3b
Answer
B
Question. ABCD is a parallelogram, A1 and B1are mid-points of side BC and CD respectively. If AA1+ BB1 = λAC then λ is equal to
(a) 1/2
(b) 1
(c) 3/2
(d) 2
Answer
C
CHAK 2
Question. If θ be the angle between the unit vectors a and b, then cos θ/2 is equal to

Answer
B
Question.
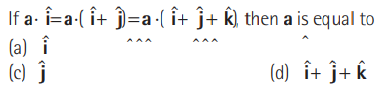
Answer
A
Question. If the scalar projection of the vector
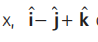
on the vector

then the value of x is equal to
(a) – 5 /2
(b) 6
(c) -6
(d) 3
Answer
A
Question.
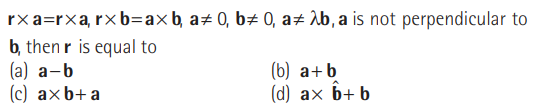
Answer
B
Question. If|a |b |c| and a+ b= c, then the angle between a and b is
(a) π /2
(b) p
(c) 0
(d) None of these
Answer
C
Question. The area of the parallelogram whose diagonals are
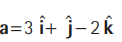
and
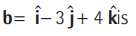
(a) 4 √3
(b) 5 √3
(c) 8
(d) 4
Answer
B
Question.

(a) 3
(b) 4
(c) 5
(d) 6
Answer
A
Question. If the vectors 2i+j+ k and i-4j+λ k are perpendicular, then λ is equal to
(a) 4
(b) -5
(c) 2
(d) 1
Answer
C
Question.

Answer
D
Question. If θ is the angle between the vectors a and band| axb|= |a,b| then θ is
(a) 0
(b) 180°
(c) 135°
(d) 45°
Answer
D
Question. The angle between two vectors a and b with magnitudes √3 and 2 respectively, having a ·b = √6 is
(a) √/4
(b) π/2
(c) π/6
(d) π/3
Answer
A
Question. If a and b are two collinear vectors, then which of the following are incorrect?
(a) b = λa, for some scalar λ
(b
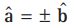
(c) The respective components of a and b are proportional.
(d) Both the vectors a and b have same direction but different magnitudes.
Answer
D
Question.
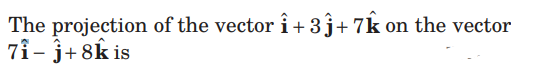
(a) 60/√122
(b) 30/√144
(c) 60/√144
(d) 60/√111
Answer
C
Question.
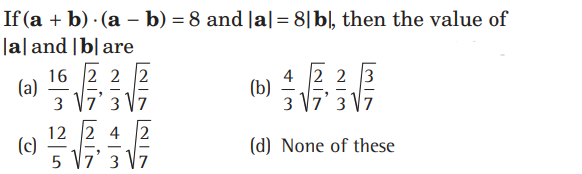
Answer
A
Question. If for a unit vector a, (x -a)· (x+a) = 12, then|x| is equal to
(a) 4
(b) 2
(c) 13
(d) 11
Answer
C
Question. The magnitude of two vectors a and b having the same magnitude and such that the angle between them is 60° and their scalar product is 1/2 are
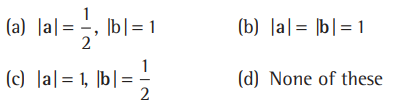
Answer
B
Question.
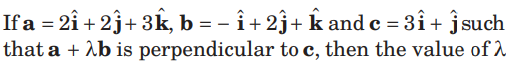
is
(a) 2
(b) 4
(c) 6
(d) 8
Answer
D
Question. For any two non-zero vectors a and b, |a |b+| b| a and |a| b-| b| a are
(a) parallel
(b) perpendicular
(c) non-parallel
(d) None of these
Answer
B
Question. If a, b c, are unit vectors such that a +b+ c = 0,then the value of a· b +b · c +c· a is
(a) 0
(b) -1/2
(c) -3/2
(d) 2/11.
Answer
C
Question. If the vertices A, B, C of a ΔABC have position vectors (1,2,3), (-1,0,0),(0,1,2) respectively, then ∠ABC (∠ABC is the angle between the vectors BA and BC), is equal to
(a)π/2
(b) π/4
(c) cos-1(10/√102)
(d) cos-1(1/3)
Answer
C
Question. If a· a× = 0 and a· b = 0, then what can be conclude about the vector b?
(a) Any vector
(b) Zero-vector
(c) Unit vector
(d) None of these
Answer
A
Question. Given that a· b = 0 and ax b = 0. What can you conclude about the vectors a and b?
(a) a and b can be perpendicular and parallel simultaneously
(b) |a| = 0 or |b| = 0
(c) |a| = 0 and |b| = 0
(d) None of the above
Answer
B
Question. A unit vector in XY-plane, making an angle of 30° in anti-clockwise direction with the positive direction of X-axis is
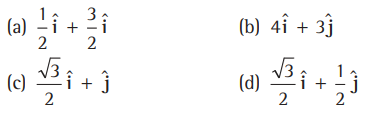
Answer
D
Question. The points A(1,2,7), B( 2,6,3) and C( 3,10,-1) are
(a) collinear
(b) coplanar
(c) non-collinear
(d) None of these
Answer
A
Question. If a = b+ c, then which of the following statements is correct?
(a) | a| =|= |c|
(b) | a|+|b| =|c|
(c) | a|b| +|c|
(d) None of these
Answer
C
Question. A vector of magnitude 5 units and parallel to
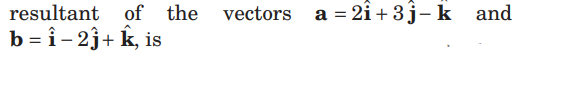
Answer
C
Question. Find the position vector of point R which divides the line joining two points p(2a+b) and Q(a-3b) externally in the ratio 1:2 . Also, show that P is the middle point of the line segment RQ.
(a) 2a + b
(b) 5a+ 3b
(c) 3a+ 5b
(d) None of these
Answer
C
Question. The value of x for which
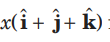
is a unit vector
a) ± 1/ √3
(b) ± 1√3
(c) ± 1/2
(d) ± 1/√2
Answer
A
Question.
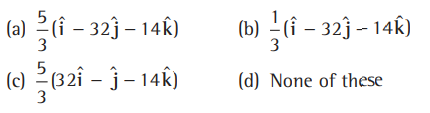
Answer
C
Question.

(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question. The two adjacent sides of a parallelogram are

Answer
A
