Circles Class 10 worksheet have been designed as per the latest pattern for CBSE, NCERT and KVS for Grade 10. Students are always suggested to solve printable worksheets for Mathematics Circles Grade 10 as they can be really helpful to clear their concepts and improve problem solving skills. We at worksheetsbag.com have provided here free PDF worksheets for students in standard 10 so that you can easily take print of these test sheets and use them daily for practice. All worksheets are easy to download and have been designed by teachers of Class 10 for benefit of students and is available for free download.
Mathematics Circles Worksheets for Class 10
We have provided chapter-wise worksheets for class 10 Mathematics Circles which the students can download in Pdf format for free. This is the best collection of Mathematics Circles standard 10th worksheets with important questions and answers for each grade 10th Mathematics Circles chapter so that the students are able to properly practice and gain more marks in Class 10 Mathematics Circles class tests and exams.
VERY SHORT ANSWER TYPE QUESTIONS
Question. In figure, PT and PS are tangents to given circle. What is the value of x?
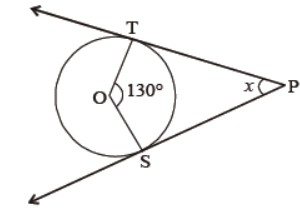
Answer
50°
Question. If figure, find the length of PB.

Answer
4 √10 cm
Question. In figure, What is the perimeter of ΔABC.
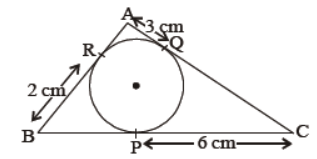
Answer
22 cm
Question. What is the distance between two parallel tangents to a circle whose radius is 4 cm.
Answer
8 cm
Question. In figure, find ∠QOR
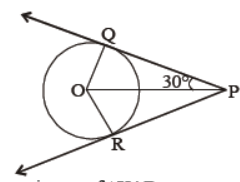
Answer
120°
Question. In figure, if XY = 25 cm, find the perimeter of ΔXAB.
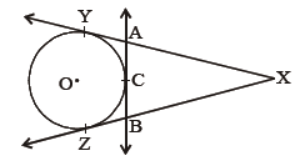
Answer
50 cm
Question. The length of a tangent PQ, from the external point P, is 24 cm. If the distance of the point P, from the centre, is 25 cm. What is the radius of the circle?
Answer
7 cm
Question. What is the minimum and maximum number of common tangents do two circles have?
Answer
0 and 4.
Question. In figure, PT is tangent to circle. What is the value of x?
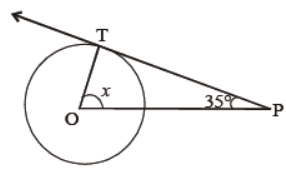
Answer
55°
Question. In figure, PQ and PR are tangents from P to a circle with centre O. What is ∠QPR.
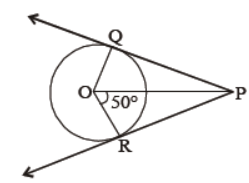
Answer
80°
Chapter-wise Class 10 Mathematics Circles Worksheets Pdf Download
Some terms associated with circle
1. Circles having the same centre but with different radii are said to be concentric circles.
2. Two circles are said to be equal or congruent if they have equal radii.
3. A circle passing through all the vertices of a polygon is called circumscribed circle of the polygon and its centre is called circumcentre.
The polygon is called inscribed polygon.
4. A circle touching all the sides of a polygon is called an inscribed circle of the polygon and its centre is called incentre.
5. The line segment joining any two points on the circumference of the circle is called a chord of the circle.
6. A chord of a circle passing through its centre is called a diameter of the circle
7. A straight line drawn from the centre of a circle to bisect a chord which is not a diameter is at right angles to chord.
8. Perpendicular drawn to a chord from the centre of a circle bisects the chord.
9. One and only one circle passes through three given points not in a straight line.
10. Equal chords are equidistant from centre.
11. Chords which are equidistant from the centre are equal in lengths.
Arc
An arc is a part of the circumference of a circle.
An arc less than one-half of the whole arc of a circle is called a minor arc of the circle, and an arc greater than one-half of the whole arc of a circle is called a major arc of the circle.

The whole arc of a circle is called the circumference of the circle.
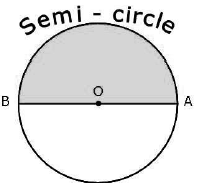
One-half of the whole arc of a circle is called a semi-circle of the circle
Segment of a Circle
A chord of a circle divides it into two parts. Each part is called a segment.
The part containing the minor arc is called the minor segment, and the part containing the major arc is called the major segment.
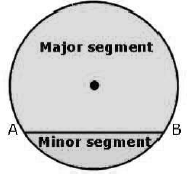
Cyclic Properties
A quadrilateral inscribed in a circle is called a cyclic quadrilateral.

The opposite angles of a cyclic quadrilateral are supplementary.
If a pair of opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
Question. Prove that the parallelogram circumscribing a circle is a rhombus.
Solution. Given: ABCD is a parallelogram.
The sides AB, BC, CD and DA touch a given circle at the point P, Q, R and S respectively.
Proof: Since lengths of the two tangents from an external point to a circle are equal.

∴ AP = AS …(i)
Q BP = BQ …(ii)
CR = CQ …(iii)
and DR = DS …(iv)
Now, AB + CD = AP + BP + CR + DR = AS + BQ + CQ + DS [Using (i), (ii), (iii) and (iv)]
= (AS + DS) + (BQ + CQ) fi AB + CD = AD + BC
But AB = CD and AD = BC [Q Opposite sides of a parallelogram are equal]
∴ AB + AB = AD + AD fi 2AB = 2AD fi AB = AD.
∴ AB = BC = CD = AD
Since all the four sides of a parallelogram ABCD are equal.
∴ ABCD is a rhombus.
Question. If two tangents inclined at an angle 60° are drawn to a circle of radius 3 cm, then find the length of each tangent.
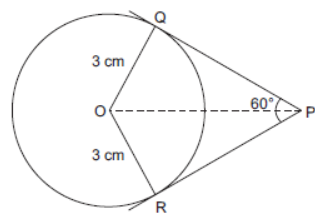
Solution. In DQPO and DRPO,
OQ = OR (Radii of same circle)
OP = OP (Common)
QP = RP (Tangents)
∴ DQPO ≅ DRPO

Question. In the figure given, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that –AOB = 90°.
Solution. Given: A circle C(O, r) in which XY and X′Y′ are parallel tangents. AB is another tangent intersecting XY
and X′Y′ at A and B respectively.
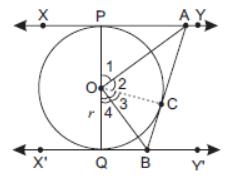
To prove: ∠AOB = 90°.
Prove: Join O and C.
In ΔAOP and ΔAOC, OP = OC (Radii of a circle)
OA = OA (Common)
∠OPA = ∠OCA (Each 90°)
∴ ΔAOP ≅ ΔAOC (By RHS Congruency)
⇒ ∠1 = ∠2 …(i) (CPCT)
Similarly, ΔBOQ ≅ ΔBOC (By RHS Congruency)
⇒ ∠3 = ∠4 …(ii) (CPCT)
Now, ∠1 + ∠2 + ∠3 + ∠4 = 180° (Angles in a straight line)
⇒ 2∠2 + 2∠3 = 180° [From (i) and (ii)]
⇒ 2(∠2 + ∠3) = 180° ⇒ ∠2 + ∠3 = 90° ⇒ ∠AOB = 90°
Hence Proved.
Question. In the given figure, PA and PB are tangents to the circle drawn from an external point P. CD is the third tangent touching the circle at Q. If PA = 15 cm, find the perimeter of DPCD.
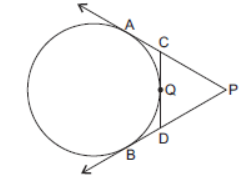
Solution. Since PA and PB are tangents from same external point P.
∴ PA = PB = 15 cm
Now, Perimeter of DPCD = PC + CD + DP = PC + CQ + QD + DP = PC + CA + DB + DP
= PA + PB = 15 cm + 15 cm = 30 cm
Question. In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
Solution. Let circle touches AC at point E and AB at point F. Join OA, OB, OC, OE and OF.
Since, the tangents to a circle from an exterior point are equal, therefore
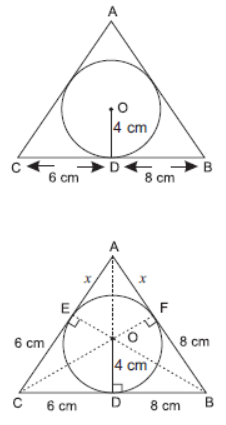
BD = BF = 8 cm, CD = CE = 6 cm
and AE = AF = x cm (let)
⇒ AC = (x + 6) cm, AB = (x + 8) cm
and BC = (6 + 8) cm = 14 cm
Now, s = AB + BC + AC/2 = x + 8 + 14 + x + 6/2
= (x + 14) cm
Also a = BC = 14 cm,
b = AC = (x + 6) cm and c = AB = (x + 8) cm
Using Heron’s formula, we get
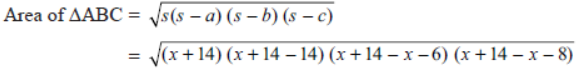
⇒ 48x(x + 14) = 16(x + 14)2 (Squaring both sides)
⇒ 3x(x + 14) = (x + 14)2
⇒ 3x(x + 14) – (x + 14)2 = 0
⇒ (x + 14) (3x – x – 14) = 0
⇒ (x + 14) (2x – 14) = 0
⇒ x + 14 = 0 or 2x – 14 = 0
⇒ x = –14 or x = 7.
As the length of any side of triangle can never be negative, x ≠ –14.
∴ x = 7 ⇒ AB = (x + 8) = 15 cm, and AC = x + 6 = 13 cm
Question. In the given figure, OP is equal to diameter of the circle. Prove that ABP is an equilateral triangle.
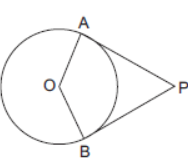
Solution. Join OP and let it meets the circle at point Q.
Since OP = 2r (Diameter of the circle)
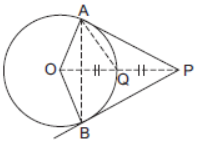
⇒ OQ = QP = r
Consider ΔAOP in which OA ⊥ AP and OP is the hypotenuse.
∴ OQ = AQ = OA
(Mid-point of the hypotenuse is equidistant from the vertices)
⇒ OAQ is an equilateral triangle.
⇒ ∠AOQ = 60° (Each angle of an equilateral triangle is 60°)
Consider right-angled triangle OAP.
∠AOQ = 60° (Proved above)
∠OAP = 90° ⇒ ∠APO = 30°
∠APB = 2∠APO = 2 × 30° = 60°
Also PA = PB (Tangents to a circle from an external point are equal.)
⇒ ∠PAB = ∠PBA (Angles opposite to equal sides in ΔPAB) In ΔABP, ∠APB = 60°
⇒ ∠PAB = ∠PBA = 180° – 60°/2 = 60°
⇒ Each angle of DPAB is 60°
⇒ PAB is an equilateral triangle. Hence Proved.
Question. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution. Let O be the common centre of two concentric circles and let AB be a chord of larger circle touching the smaller circle at P. Join OP.
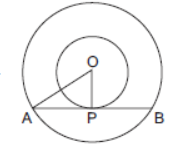
Since OP is the radius of the smaller circle and AB is a tangent to this circle at P.
∴ OP ⊥ AB
Since perpendicular drawn from the centre of a circle to any chord of the circle bisects the chord.
⇒ AP = PB
Now, in DAOP, right-angled at P,
OA2 = AP2 + OP2 ⇒ 52 = AP2 + 32 ⇒ 25 – 9 = AP2
⇒ AP2 = 16 fi AP = 4
Now AB = 2 × AP = 2 × 4 = 8 [∴ AP = PB]
Hence, the length of the chord of the larger circle which touches the smaller circle is 8 cm.
Question. Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Solution. Construction: Join OA and OB.
Proof: As we know, OB is perpendicular to PQ.
[Tangent is perpendicular to radius
at the point of contact.]
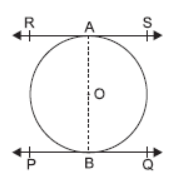
Now, given, PQ || RS
⇒ BO (produced to RS) is perpendicular to RS. …(i)
[A line perpendicular to one of the two parallel lines is
perpendicular to other line also]
Also, OA is perpendicular to RS.
[Q Tangent perpendicular to radius] …(ii) (1)
From (i) and (ii), OA and OB must coincide as only one
line can be drawn perpendicular to the line from a point
outside the line.
∴ AOB is straight line.
∴ A, O, B are collinear.
⇒ AB passes through O, the centre of the circle.
Question. In the given figure, AP and BP are tangents to a circle with centre O, such that AP = 5 cm and –APB = 60°. Find the length of chord AB.

Solution. 5 cm
Question. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q, so that OQ = 12 cm. Find the length of PQ.
Solution. Since PQ = √OQ2 – OP2 = √122 − √52
Question. In the given figure, O is the centre of the circle. Determine –AQB and –AMB, if PA and PB are tangents and –APB = 75°
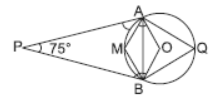
Solution. –AQB = 52.5°, –AMB = 127.5°
Question. In the given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.
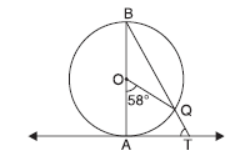
Solution. ∴ AT is a tangent and BA is a diameter.
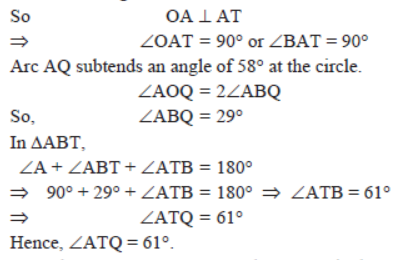
Question. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. Find the radius of the circle.
Solution. ∴ Using Pythagoras theorem, we get
OQ2 = QT2 + OT2
⇒ OT2 = OQ2 – QT2
= 252 – 242
= (25 – 24) (25 + 24)
= 1 × 49 = 49
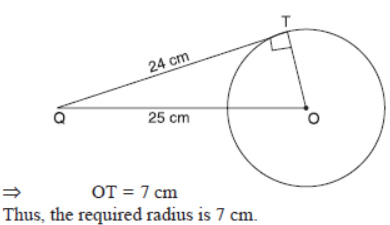
Question. Prove that the tangents at the extremities of a chord of a circle make equal angles with the chord.
Solution. We know that tangents drawn from an external point P to a circle are equal so PA = PB.
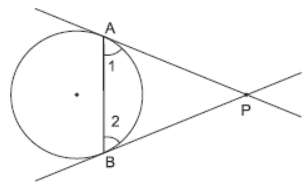
⇒ ∠2 = ∠1
[Angles opposite to equal sides of a triangle are equal]
Hence, tangents PA and PB make equal angles with chord AB.
Hence proved.
Question. In the given figure, a circle inscribed in DABC, touches its sides BC, CA and AB at the points P, Q and R respectively. If AB = AC, then prove that BP = CP.
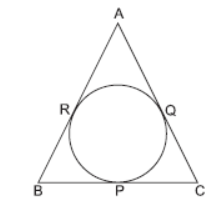
Solution. AB = AC
⇒ AR + BR = AQ + CQ
⇒ AR + BR = AR + CQ [AQ = AR equal tangents]
⇒ BR = CQ (1)
Now, BR = BP [Length of equal tangents]
and CQ = CP
⇒ BP = CP
Question. In the given figure, DABC is circumscribing a circle. Find the length of BC.
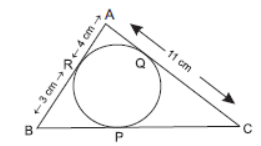
Solution. BP = BR = 3 cm
AQ = AR = 4 cm
⇒ CQ = 11 cm – 4 cm = 7 cm
⇒ CP = CQ = 7 cm
Hence, BC = BP + CP = (3 + 7) = 10 cm
Question. A circle is inscribed in a ΔABC having sides 8 cm, 10 cm and 12 cm as shown in the following figure. Find AD, BE and CF.
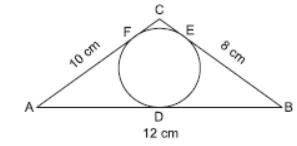
Solution. Let AD = x1, BE = x2 and CF = x3;
then AF = AD = x1, BD = BE = x2
and CE = CF = x3.
∴ x1 + x2 = 12; x2 + x3 = 8; x1 + x3 = 10
Adding,
2(x1 + x2 + x3) = 30
⇒ x1 + x2 + x3 = 15
Solve for x1, x2 and x3 to get
AD = 7 cm, BE = 5 cm,
CF = 3 cm
Question. PC is a tangent to the circle at C. AOB is the diameter which when extended meets the tangent at P. Find ∠CBA, ∠AOC and ∠BCO, if ∠PCA = 110°.
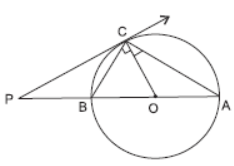
Solution. –AOC = 140°, –CBA = 70° = –BCO
Question. From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of the line segment PQ.
Solution. TP and TQ are tangents at P and Q respectively.
So, OP ^ PT and OQ ^ QT
∴ ∠OPT = ∠OQT = 90°
In DOPT and DOQT
OP = OQ (Radius)
∠P = ∠Q (Each 90°)
OT = OT (Common)
So, DOPT ≅ DOQT (RHS)
⇒ ∠1 = ∠2
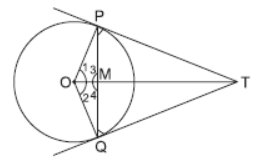
Now, in DOMP and DOMQ,
OP = OQ (Radius)
∠1 = ∠2 (Proved above)
OM = OM (Common)
So, DOMP ≅ DOMQ (SAS)
⇒ PM = MQ and ∠3 = ∠4
Now ∠3 + ∠4 = 180° (Q Linear Pair Axiom)
⇒ 2∠3 = 180° ⇒ ∠3 = 90°
⇒ ∠OMP = 90°
Hence, OT is the right bisector of the line segment PQ.
Question. Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
Solution.

Question. In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length of TP.
Solution. Given: PQ = 8 cm and PO = 5 cm
Now, PR = RQ (Perpendicular from the
centre bisects the chord)
= 8/2 = 4 cm


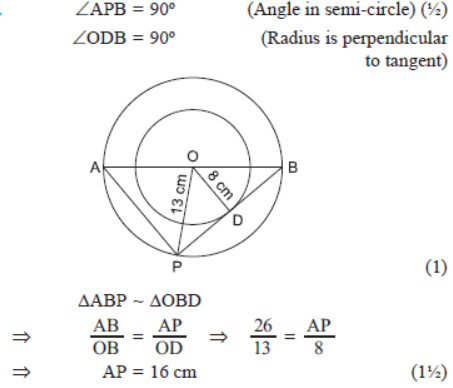
Question. The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle. BD is a tangent to the smaller circle, touching it at D and intersecting the larger circle at P on producing. Find the length of AP.
Solution.
Question. From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Solution. Given, ∠PAB = 50°
∠PAB + ∠OAB = 90°
[∴ an angle between radius
OA and tangent PA is 90°]
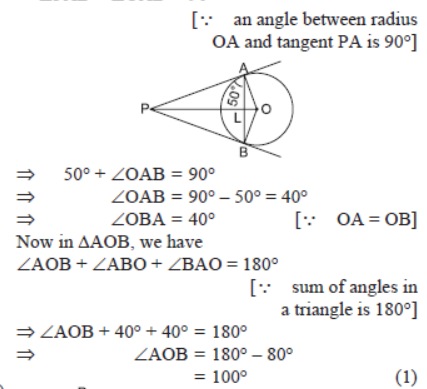
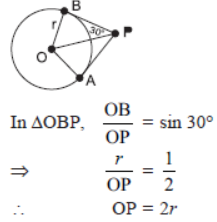
Question. If the angle between two tangents drawn from an external point ‘P’ to a circle of radius ‘r’ and centre O is 60°, then find the length of OP.
Solution.
Question. In the given figure, common tangents AB and CD to two circles with centres O1 and O2 intersect at E. Prove that AB = CD.
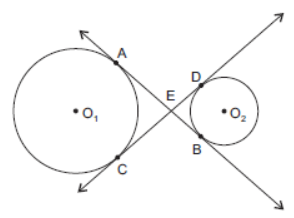
Solution. AB and CD are common tangents to the two given circles
with centres O1 and O2 respectively (refer to question for figure).
We know that the lengths of the tangents drawn from a
point outside the circle to the circle are equal in length.
∴ AE = EC and EB = ED (1)
⇒ AE + EB = CE + ED ⇒ AB = CD
Question. If the radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle.
Solution. Length of chord
= 2 × √52 – 42
= 2 × 3 cm = 6 cm
Question. In the given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If ∠PRQ = 120°, then prove that OR = PR + RQ.
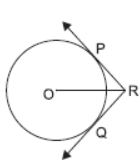
Solution. OR bisects ∠PRQ
∴ ∠PRO = ∠QRO = 60°
[∴ ∠PRQ = ∠ORP + ∠ORQ = 120°]

Question. If PQ = 28 cm, then find the perimeter of DPLM.
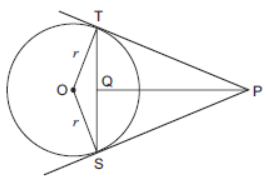
Solution. PQ = PT
PL + LQ = PM + MT
PL + LN = PM + MN
Perimeter (DPLM) = PL + LM + PM (½)
= PL + LN + MN + PM
= 2(PL + LN)
= 2(PL + LQ)
= 2 × 28 = 56 cm
Question. PQ is a tangent to a circle with centre O at point P. If DOPQ is an isosceles triangle, then find ∠OQP.
Solution. In ΔOPQ 6
Question. In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70°,find ∠TRQ.

Solution. We know that tangent is perpendicular to radius. Hence,
∠OTP = ∠OQP = 90°
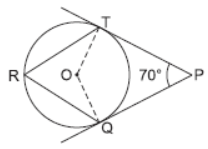
In quadrilateral PQOT,
∠QOT + ∠OTP + ∠TPQ + ∠OQP = 360°
⇒ ∠TOQ + ∠TPQ = 180° ⇒ ∠TOQ = 110°
Also ∠TOQ = 2∠TRQ
⇒ 110º = 2∠TRQ
⇒ ∠TRQ = 55°
Question. In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
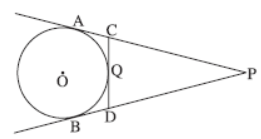
Solution. PA = PC + CA = PC + CQ
⇒ 12 = PC + 3
⇒ PC = 9 cm (1)
Similarly, PD = 9 cm
∴ PC + PD = 18 cm
Question. A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA .
Solution. Here AP = AS
BP = BQ
CR = CQ
DR = DS
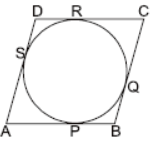
Adding (AP + PB) + (CR + RD)
= (AS + SD) + (BQ + QC)
⇒ AB + CD = AD + BC
Question. In the given figure, find the perimeter of DABC, if AP = 12 cm.

Solution. Since AP and AQ are two tangents drawn from common external point A.

∴ AP = AQ = 12 cm (Given)
Similarly, BP = BD …(i)
and CQ = CD …(ii) (1)
Now perimeter of
DABC = AB + BC + AC
= AB + BD + CD + AC
= AB + BP + CQ + AC
[From (i) and (ii)]
= AP + AQ = 12 + 12
= 24 cm
Question. In the given figure, a circle touches all the four sides of a quadrilateral ABCD in which AB = 6 cm, BC = 7 cm and CD = 4 cm. Find AD.
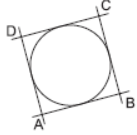
Solution. 3 cm
Question. If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that –QPR = 120°, prove that 2PQ = PO.
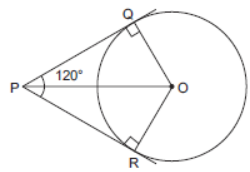
Solution. Proof: In triangle OQP and ORP,
OQ = OR = r (say) [Radii]
OP = OP (Common)
PQ = PR
[The lengths of the tangents drawn from an external point to a circle are equal]
∴ DOQP ≅ DORP
∴ ∠OPQ = ∠OPR
Now, given ∠QPR = 120°
⇒ ∠OPQ + ∠OPR = 120°
⇒ 2∠OPQ = 120°
⇒ ∠OPQ = 60° = ∠OPR
Now, in DOQP, ∠Q = 90°
[∴ Tangent is perpendicular to radius]
Then, PQ/OP = cos 60° = 1/2
⇒ OP = 2PQ
Question. Using the given figure, answer the following questions:
(i) Name the alternate segment of circle of ∠BAQ
(ii) Name the alternate segment of circle of ∠DAP.
(iii) If B is joined with C then ∠ACB is equal to which angle?
(iv) ∠ABD and ∠ADB is equal to which angles?

Solution. (i) ∠ADB (ii) ∠ABD
(iii) ∠BAP (iv) ∠DAP and ∠BAQ
Question. A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.
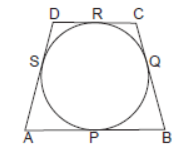
Solution. To prove: AB + CD = AD + BC
Proof: AS = AP (Length of tangents from an
external point to a circle are equal)
BQ = BP
CQ = CR
DS = DR (1)
AS + BQ + CQ + DS = AP + BP + CR + DR
(AS + DS) + (BQ + CQ)
= (AP + BP) + (CR + DR)
AD + BC = AB + CD
Question. A circle is touching the side BC of ΔABC at X and touching AB and AC produced at P and Q respectively. Prove that AP = AQ = 1/2 (Perimeter of ΔABC). Given AP = 10 cm, find the perimeter of ΔABC.
Solution. In the given figure,
AP = AQ, BP = BX and CX = CQ
⇒ AB + BX = AC + CX …(i) (1)
∴ Perimeter of
ΔABC = AB + BC + CA
= AB + (BX + XC) + CA
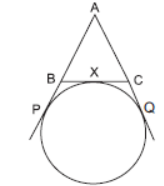
= (AB + BX) + (XC + CA)
= 2(AB + BX), using (i).
Hence, AP = 1/2 × (perimeter of DABC) = AQ.
If AP = 10 cm, then perimeter of ΔABC = 20 cm.
Question. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution. In right D OAP and right D OBP, we have
PA = PB [Tangents to circle from
an external point P]
OA = OB [Radii of the same circle]
OP = OP [Common]
∴ By SSS congruency,
DOAP ≅ DOBP
and ∠AOP = ∠BOP
⇒ ∠APB = 2 ∠OPA
and ∠AOB = 2 ∠AOP (1)
But ∠AOP = 90° – ∠OPA
⇒ 2∠AOP = 180° – 2∠OPA
⇒ ∠AOB = 180° – ∠APB
⇒ ∠AOB + ∠APB = 180°.
Question. In the figure, quadrilateral ABCD is circumscribing a circle with centre O and AD ^ AB. If radius of incircle is 10 cm, then find the value of x.

Solution. ∠A = ∠OPA = ∠OSA = 90° (½)
Hence, ∠SOP = 90°
Also, AP = AS
Hence, OSAP is a square
AP = AS = 10 cm (½)
CR = CQ = 27 cm
BQ = BC – CQ
= 38 – 27 = 11 cm (½)
BP = BQ=11 cm
x = AB = AP + BP
= 10 + 11 = 21 cm
Question. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution. In the figure, we have:
PQ is diameter of the given circle and O is its centre.
Let tangents AB and CD be drawn at the end points of the diameter PQ.
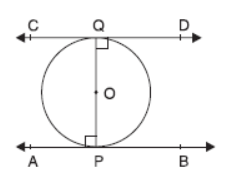
Since the tangent at a point to a circle is perpendicular to
the radius through the point.
∴ PQ ⊥ AB ⇒ ∠APQ = 90°
and PQ ⊥ CD ⇒ ∠PQD = 90°
⇒ ∠APQ = ∠PQD
But they form a pair of alternate angles.
∴ AB || CD.
Question. In the given figure, from an external point P, a tangent PT and a line segment PAB are drawn to a circle with centre O. ON is perpendicular on the chord AB. Prove that
(a) PA · PB = PN2 – AN2
(b) PN2 – AN2 = OP2 – OT2
(c) PA · PB = PT2
Solution. (a) PA · PB = (PN – AN) (PN + BN)
= (PN – AN)(PN + AN) (As AN = BN)
⇒ PA.PB = PN2 – AN2 …(i) (1)
(b) PN2 – AN2 = (OP2 – ON2) – AN2 (As ON ⊥ PN)
= OP2 – (ON2 + AN2) (1)
= OP2 – OA2 (As ON ⊥ AN)
⇒ PN2 – AN2 = OP2 – OT2 (As OA = OT) …(ii)
(c) From (i) and (ii)
PA . PB = OP2 – OT2 = PT2 (As ∠OTP = 90°)
Question. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution. Given: ABCD is a quadrilateral circumscribing the circle
with centre O touching it at P, Q, R, S.

To prove:
∠AOB + ∠DOC = 180°
∠AOD + ∠BOC = 180°
Construction: Join AO, PO, BO, QO, CO, RO, DO, SO.
Proof: In DAOS and DAOP,
AO = AO (Common)
AS = AP
(Tangents from external point)
OS = OP (Radii of same circle)
By SSS congruence rule,
DAOS ≅ DAOP
∠1 = ∠2 …(i) (by CPCT) (1)
Similarly, ∠3 = ∠4, ∠5 = ∠6, ∠7 = ∠8 …(ii)
Now,
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
[∴ ASP of quadrilateral]
⇒ ∠2 + ∠2 + ∠3 + ∠3 + ∠6 + ∠6 + ∠7 + ∠7 = 360°
[By (i) and (ii)]
⇒ 2[∠2 + ∠3 + ∠6 + ∠7] = 360°
∠AOB + ∠COD = 180°
Similarly, ∠AOD + ∠BOC = 180°
Question. Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
Solution. Given: Let O be the centre of two concentric circles C1 and C2.
Let AB be the chord of larger circle C2 which is a tangent
to the smaller circle C1 at D.

To prove: Now we have to prove that the chord AB is
bisected at D that is AD = BD. (1)
Construction: Join OD.
Proof: Now since OD is the radius of the circle C1 and
AB is the tangent to the circle C1 at D.
So, OD ⊥ AB
[Radius of the circle is perpendicular
to tangent at any point of contact]
Since AB is the chord of the circle C2 and OD ⊥ AB.
∴ AD = DB
[Perpendicular drawn from the centre to
the chord always bisects the chord]
Question. In the given figure, a circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths of QM, RN and PL.
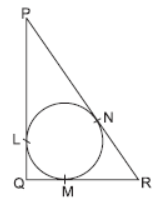
Solution. Let QM = x = QL
MR = y = RN
and PL = z = PN
Now PQ = 10 cm,
QR = 8 cm,
PR = 12 cm
⇒ x + y = 8, y + z = 12, z + x = 10
⇒ 2x + 2y + 2z = 8 + 12 + 10 = 30
⇒ x + y + z = 15 ⇒ 8 + z = 15
⇒ z = 7
⇒ x + 12 = 15 ⇒ x = 3
⇒ y + 10 = 15 ⇒ y = 5
Hence, QM = 3 cm, RN = 5 cm and PL = 7 cm.
Question. If d1, d2, (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, prove that d22 = c2 + d21
Solution. Q Diameter of bigger circle = d2

Question. A circle touches the side BC of a DABC at P and AB and AC when produced at Q and R respectively as shown in the figure. Show that AQ = 1/2 (Perimeter of DABC)

Solution. We have BQ = BP, CP = CR and AQ = AR

Now, 2AQ = AQ + AR
= (AB + BQ) + (AC + CR) (1)
= AB + BP + AC + CP
= (BP + CP) + AC + AB (1)
= BC + CA + AB
i.e. AQ = 1/2 (BC + CA + AB)
Question. In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.
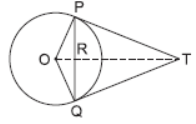
Solution. Join OT intersecting PQ at R.
OT bisects ∠PTQ
∴ ∠PTO = ∠QTO
∴ ∠PTR = ∠QTR
In DPTR and DQTR,
PT = QT [Length of tangents drawn from
common external point are equal]
RT = RT [common] (1)
∠PTR = ∠QTR [ from (i)]
∴ DPTR ≅ DQTR
⇒ PR = RQ
Question. Two concentric circles are of radii 7 cm and r cm respectively, where r > 7 cm. A chord of the larger circle, of length 48 cm, touches the smaller circle. Find the value of r.
Solution. Given: OP = 7 cm, OA = r cm
AB = 48 cm
Now OP ⊥ AB
(as radius makes an angle of 90° with
the tangent at point of contact)
Also, AP = PB
(Perpendicular drawn from centre
to the chord bisects the chord)
So, AP = 24 cm

In DOPA, ∠P = 90° (1)
By Pythagoras theorem in DOPA,
OA2 = AP2 + OP2
r2 = 242 + 72
= 576 + 49 = 625
⇒ r = 25 cm
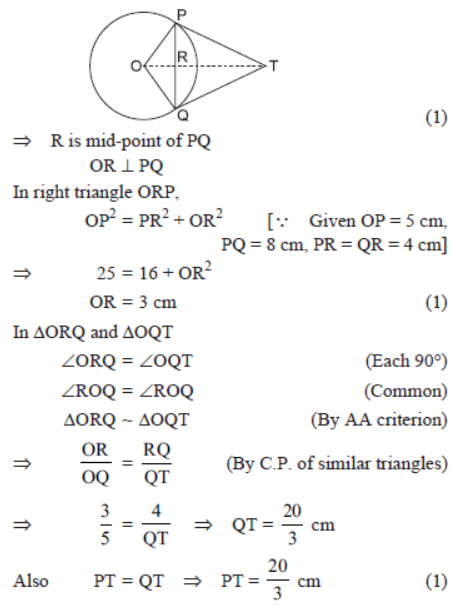
Question. In the given figure, PA and PB are two tangents drawn from an external point P to a circle with centre O. Prove that OP is the right bisector of line segment AB.

Solution. Join OA and OB.
In DPAO and DPBO,
OA = OB
OP = OP
and AP = BP [Tangents from P]
∴ DPAO ≅ DPBO
⇒ ∠1 = ∠2
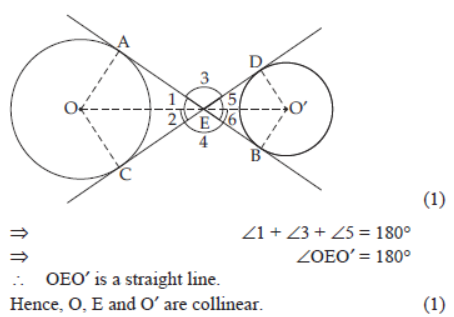
Question. In the given figure, common tangents AB and CD of two circles with centres O and O′ intersect at E. Prove that the points O, E and O′ are collinear.
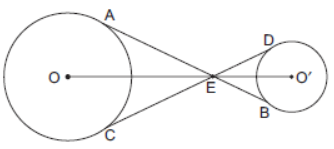
Solution. In DAEO and DCEO,
OE = OE [Common]
OA = OC [Radii of same circle]
EA = EC [Tangents from an external point
to a circle are equal in length]
∴ DOEA ≅ DOEC
[By SSS criterion of congruence]
⇒ ∠OEA = ∠OEC [CPCT]
∴ ∠1 = ∠2 [CPCT] (1)
Similarly, ∠5 = ∠6
and ∠3 = ∠4 [Vertically opposite angles]
Since sum of angles at a point = 360°
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°
⇒ 2(∠1 + ∠3 + ∠5) = 360°
Question. If a number of circles pass through the end points P and Q of a line segment PQ, then show that their centres lie on the perpendicular bisector of PQ.
Solution. Centre of any circle passing through the end points P and Q of a line segment are equidistant from P and Q.
∴ A1P = A1Q
A2P = A2Q
A3P = A3Q
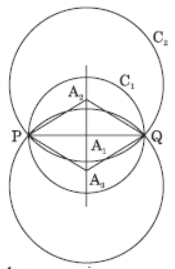
As we know that any point on perpendicular bisector of a segment is equidistant from the end points of the segment.
Hence, A1, A2, A3 points are the centres of circles passing through the end points P and Q of a segment PQ or the centres of circles lie on the perpendicular bisector of PQ.
Question. If a, b, c, are the sides of a right-angled triangle, where c is the hypotenuse, then prove that the radius r of the circle which touches the sides of the triangle is given by r = a + b – c/2
Solution. Let the circle touches the sides BC, CA, AB of the right
triangle ABC at D, E and F respectively, where BC = a,
CA = b and AB = c (see figure). Then AE = AF and BD
= BF. Also CE = CD = r.

Question. Two concentric circles of radii 13 cm and 12 cm, are given. Find the length of chord of the larger circle which touches smaller circle.
Solution. 10 cm
Mathematics Circles Worksheets for Class 10 as per CBSE NCERT pattern
Parents and students are welcome to download as many worksheets as they want as we have provided all free. As you can see we have covered all topics which are there in your Class 10 Mathematics Circles book designed as per CBSE, NCERT and KVS syllabus and examination pattern. These test papers have been used in various schools and have helped students to practice and improve their grades in school and have also helped them to appear in other school level exams. You can take printout of these chapter wise test sheets having questions relating to each topic and practice them daily so that you can thoroughly understand each concept and get better marks. As Mathematics Circles for Class 10 is a very scoring subject, if you download and do these questions and answers on daily basis, this will help you to become master in this subject.
Benefits of Free Circles Class 10 worksheet
- You can improve understanding of your concepts if you solve NCERT Class 10 Mathematics Circles Worksheet,
- These CBSE Class 10 Mathematics Circles worksheets can help you to understand the pattern of questions expected in Mathematics Circles exams.
- All worksheets for Mathematics Circles Class 10 for NCERT have been organized in a manner to allow easy download in PDF format
- Parents will be easily able to understand the worksheets and give them to kids to solve
- Will help you to quickly revise all chapters of Class 10 Mathematics Circles textbook
- CBSE Class 10 Mathematics Circles Workbook will surely help to improve knowledge of this subject
These Printable practice worksheets are available for free download for Class 10 Mathematics Circles. As the teachers have done extensive research for all topics and have then made these worksheets for you so that you can use them for your benefit and have also provided to you for each chapter in your ebook. The Chapter wise question bank and revision worksheets can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Circles Worksheets PDF.

You can download free worksheets for Class 10 Mathematics Circles from https://www.worksheetsbag.com
You can get free PDF downloadable worksheets for Grade 10 Mathematics Circles from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided worksheets for all subjects in Grade 10, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.worksheetsbag.com without any charge
Yes all test papers for Mathematics Circles Class 10 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all worksheets.
https://www.worksheetsbag.com is the best portal to download all worksheets for all classes without any charges.