Heron’s Formula Class 9 Worksheet with Answers have been designed as per the latest pattern for CBSE, NCERT and KVS for Grade 9. Students are always suggested to solve printable worksheets for Mathematics Herons Formula Grade 9 as they can be really helpful to clear their concepts and improve problem solving skills. We at worksheetsbag.com have provided here free PDF worksheets for students in standard 9 so that you can easily take print of these test sheets and use them daily for practice. All worksheets are easy to download and have been designed by teachers of Class 9 for benefit of students and is available for free download.
Mathematics Herons Formula Worksheets for Class 9
We have provided chapter-wise worksheets for class 9 Mathematics Herons Formula which the students can download in Pdf format for free. This is the best collection of Mathematics Herons Formula standard 9th worksheets with important questions and answers for each grade 9th Mathematics Herons Formula chapter so that the students are able to properly practice and gain more marks in Class 9 Mathematics Herons Formula class tests and exams.
Chapter-wise Class 9 Mathematics Herons Formula Worksheets Pdf Download
1. Area of a Triangle – by Heron’s Formula
2. Application of Heron’s Formula in finding Areas of Quadrilaterals
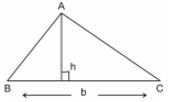
• Triangle with base ‘b’ and altitude ‘h’ is
Area = 1/2X(bXh)
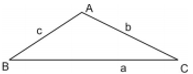
• Triangle with sides a, b and c
(i) semi perimeter of triangle s = a + b + c/2
(ii) Area = √8(8 – a) (8 – b) (s – c) square units.
• Equilateral triangle with side ‘a’ Area = √3/4, a2 square units
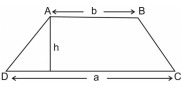
• Trapezium with parallel sides ‘a’ & ‘b’ and the distance between two parallel sides as ‘h’. Area = 1/7 (a + b) h square units
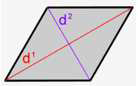
• Rhombus with diagonals d1 and d2
Area = 1/2, d1 X d2;
perimeter = 2√d21 + d22
Question. The perimeter of an equilateral triangle is 60 m, then its area is:
(a) 10√3m2
(b) 15√3m2
(c) 20√3m2
(d) 100√3m2
Answer
D
Question. The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is
(A) 1322 cm2
(B) 1311 cm2
(C) 1344 cm2
(D) 1392 cm2
Answer
C
Question. An isosceles right triangle has area 8 cm2. The length of its hypotenuse is
(a) √32cm
(b) √16cm
(c) √48cm
(d) √24cm
Answer
A
Question. The length of each side of an equilateral triangle having an area of 9√3cm2 is
(A) 8 cm
(B) 36 cm
(C) 4 cm
(D) 6 cm
Answer
D
Question. If the area of an equilateral triangle is 16√3cm2 then the perimeter of the triangle is
(A) 48 cm
(B) 24 cm
(C) 12 cm
(D) 36 cm
Answer
B
Question. The area of an equilateral triangle with side 2√3cm is
(a) 5.196 cm2
(b) 0.886 cm2
(c) 3.496 cm2
(d) 1.732 cm2
Answer
A
Question. The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude
(a) 16√5cm
(b) 10√5cm
(c) 24√5cm
(d) 28 cm
Answer
C
Question. The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm2 is
(A) Rs2.00
(B) Rs2.16
(C) Rs2.48
(D) Rs3.00
Answer
B
Question. The area of an isosceles triangle having base 2 cm and the length of its equal sides 4cm, is
(a) √15cm2
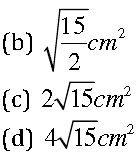
Answer
A
Question. The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
Answer. The base of the parallelogram is 10 cm and the corresponding altitude is 3.5 cm.
Area of || gm = base × corresponding altitude.
= 10 cm × 3.5 cm = 35 cm2.
Hence, the given statement is false.
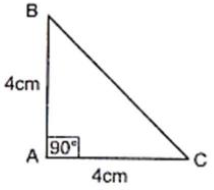
Question. The area of Δ ABC is 8 cm2 in which AB = AC = 4 cm and ∠A= 90º.
Answer. Area of Δ = 1/2 X base X height = 1/2 X 4 X 4 = 8cm2
Hence, the given statement is true.
Question. The area of the isosceles triangle is 5/4 √11cm2 if the perimeter is 11 cm and the base is 5 cm.
Answer. Let the equal sides of the isosceles triangle be ‘a’ and base of the triangle be ‘b’.
Perimeter of Δs = 5 + a + a = 11
⇒ 2a = 11 − 5 = 6;a = 6 ÷ 2 = 3cm
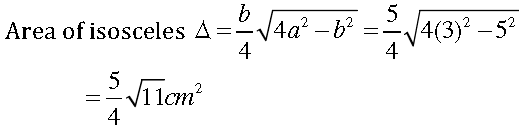
Hence, the given statement is true.
Question. If the side of a rhombus is 10 cm and one diagonal is 16 cm, the area of the rhombus is 96 cm2.
Answer. Let ABCD be the rhombus whose one diagonal AC is 16cm. Each side of rhombus is 10cm. We know that diagonal of a rhombus bisect each other at right angles, so OA = OC = 8 cm and OB = OD.
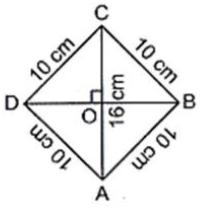
In ΔAOB, we have ∠AOB = 900
∴ AB2 = OA2 +OB2
⇒ OB2 = AB2 −OA2
= (10)2 −82 =100 − 64 = 36
∴ OB = + √36 = 6cm
∴ DB = 2(OB) = 2 × 6 =12cm
Hence, area of rhombus = 1/2 × Product of diagonals
= 1/2 x 16 x 12 = 96cm2
Hence, the given statement is true.
Question. The area of a triangle with base 4 cm and height 6 cm is 24 cm2.
Answer. Area of Δ = 1/2 X base X height = 1/2 X 4X 6 = 12cm2
Hence, the statement is false.
Question. The area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a.
Answer. We see a regular hexagon is divided into six equilateral triangles.
So, the area of the regular hexagon is divided side ‘a’ is the sum of area of the six equilateral triangles with side a.
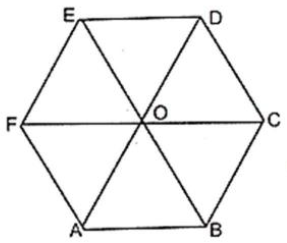
Hence, the given statement that the area of a regular hexagon of side ‘a’ is the sum of the areas of the five equilateral triangles with side a is false.
Question. The area of the equilateral triangle is 20√3cm2 whose each side is 8 cm.
Answer. Area of equilateral = √3/4 (side)2
= √3/4 (8)2 = √3/4 X 64 = 16 √3cm2
Hence, the given statement is false.
Question. In a triangle, the sides are given as 11 cm, 12 cm and 13 cm. The length of the altitude is 10.25 cm corresponding to the side having length 12 cm.
Answer. We have the length of the altitude corresponding to the side having length 12 cm.
2s = 11 cm + 12 cm + 13 cm = 36 cm
⇒ s = 36 ÷ 2 = 18cm
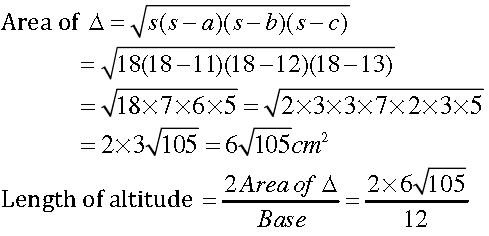
= √105 =10.25cm
Hence, the given statement is true.
Question. Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of Rs 7 per m2.
Answer. We have, 2s = 50 m + 65 m + 65 m = 180 m
S = 180 ÷ 2 = 90 m
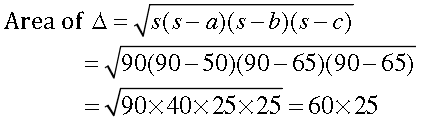
= 1500m2.
Cost of laying grass at the rate of Rs 7 per m2 = Rs (1500 × 7) = Rs 10,500
Question. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of Rs 2000 per m2 a year. A company hired one of its walls for 6 months. How much rent did it pay?
Answer. The sides of triangular side walls of flyover which have been used for advertisements are 13 m, 14 m, 15 m.
s = 13 + 14 + 15 / 2 = 42 / 2 = 21 m
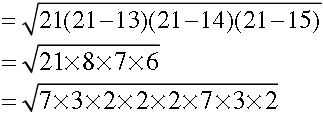
= 7 × 3 × 2 × 2 = 84m2
It is given that the advertisement yield an earning of Rs 2,000 per m2 a year.
∴ Rent for 1 m2 for 1 year = Rs 2000
So, rent for 1 m2 for 6 months or 1/2 year = rs (1/2 x 2000) = Rs 1,000.
∴ Rent for 84 m2 for 6 months = Rs (1000 × 84) = Rs 84,000.
Question. The cost of levelling the ground in the form of a triangle having the sides 51 m, 37 m and 20 m at the rate of Rs 3 per m2 is Rs 918.
Answer. We have 2s = 51 m + 37 m + 20 m= 180 m
⇒ 108 ÷ 2 = 54m
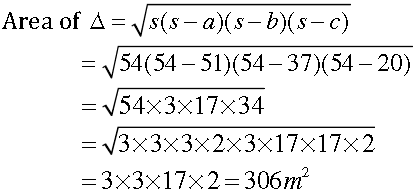
Cost of leveling the ground = Rs (306 × 3) Rs 918
Hence, the given statement is true.
Question. From a point in the interior of an equilateral triangle, perpendiculars are drawn on the three sides. The lengths of the perpendiculars are 14 cm, 10 cm and 6 cm.
Find the area of the triangle.
Answer. Let ABC be an equilateral triangle, O be the interior point and OQ, OR and OC are the perpendicular drawn from points O. Let the sides of an equilateral triangle be a m.
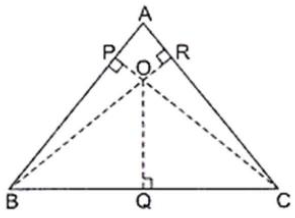
Area of ΔAOB = 1/2 × AB × OP
[∵ Area of a triangle = 1/2 x (base × height)]
= 1/2 × a × 14 = 7 a cm2 …(1)
Area of ΔOBC = 1× BC × OQ 1/2 × a × 10
= 5a cm2 …(2)
Area of ΔOAC = 1/2 × AC × OR = 1/2 × a × 6
= 3a cm2 …(3)
∴ Area of an equilateral ΔABC
= Area of (ΔOAB + ΔOBC + ΔOAC)
= (7a + 5a + 3a) cm2
= 15a cm2 …(4)
We have, semi-perimeter s = a + a + a / 2
⇒ s = (3a/2) cm
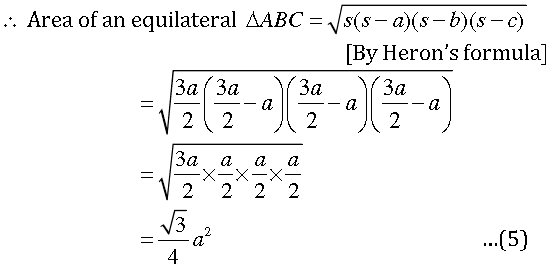
From equations (4) and (5), we get
√3 / 4 a2 = 15a
⇒ a = 15 x 4 / √3 = 60 / √3
⇒ a = 60 / √3 = √3 / √3 = 20√3cm
On putting a = 20√3 in equation (5), we get
Area of ΔABC = √3 (20√3)2 = √3 / 4 x 400 x 3 = 300√3cm2
Hence, the area of an equilateral triangle is 300√3cm2.
Question. Find the area of a parallelogram given in Fig. 12.2. Also find the length of the altitude from vertex A on the side DC.
Answer. Area of parallelogram ABCD = 2 (Area of ΔBCD) …(1)
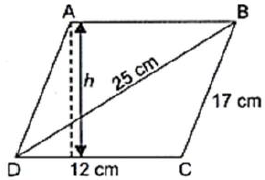
Now, the sides of ΔBCD are
a = 12 cm, b = 17 cm and c = 25 cm.
∴ Semi-perimeter of ΔBCD,
s = a + b + c / 2
= 12 + 17 + 25 / 2
= 54 / 2 = 27cm
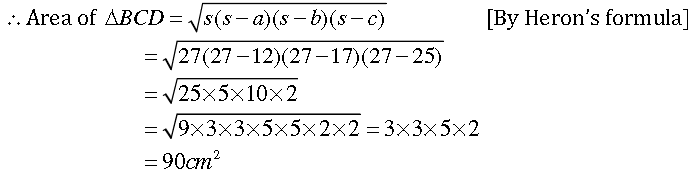
From equation (1), we get
Area of parallelogram ABCD = 2 x 90 = 180cm2
Let the altitude of parallelogram be h.
Also, area of parallelogram ABCD = Base × Altitude
⇒ 180 = DC × h
⇒ 180 = 12× h
⇒ h = 180 / 12 = 15cm
Hence, the area of parallelogram is 180 cm2 and the length of altitude is 15 cm.
Question. A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
Answer. Let the field be ABCD.
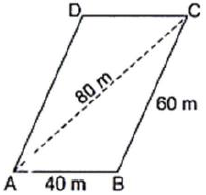
Area of the parallelogram ABCD = 2(area of ΔABC ) …(1)
Now, the sides of ΔABC are
a = 40 m, b = 60 m and c = 80 m
∴ Semi-perimeter of ΔABC,
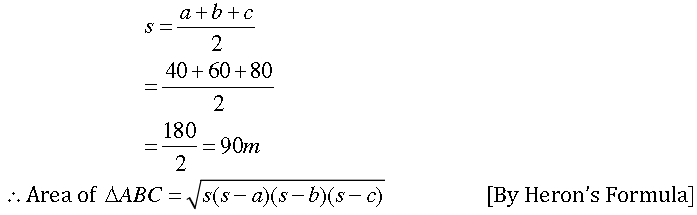
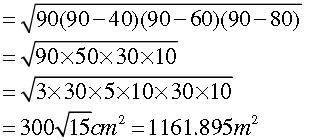
Formula equation (1), we get
Area of parallelogram ABCD = 2 × 1161.895 = 2323.79 m2.
Question. The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3: 2. Find the area of the triangle.
Answer. As the sides of the equal to the base of an isosceles triangle is 3: 2, so let the sides of an isosceles triangle be 3x, 3x and 2x.
Now, perimeter of triangle = 3x + 3x + 2x = 8x
Given Perimeter of triangle = 32 m
∴ 8x = 32; x = 32 ÷8 = 4
So, the sides of the isosceles triangle are (3×4)cm, (3×4)cm, (2×4)cm i.e., 12 cm, 12 cm and 8cm
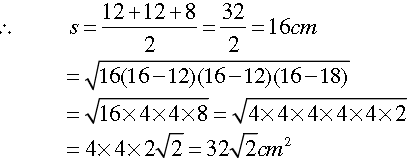
Question. The perimeter of a triangular field is 420 m and its sides are in the ratio 6 : 7 : 8.
Find the area of the triangular field.
Answer. Suppose that the sides in metres are 6x, 7x and 8x.
Now, 6x + 7x + 8x = perimeter = 420
⇒ 21x = 420
⇒ x = 420/21
⇒ x = 20
∴ The sides of the triangular field are 6 × 20m,7× 20m, 8 × 20m, i.e., 120 m, 140 m and 160m.
Now, s = Half the perimeter of triangular field
= 1/2 x 420m = 210
Using Heron’s formula,
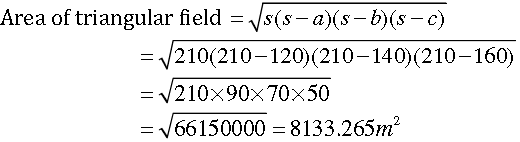
Hence, the area of the triangular field = 8133.265 m2.
Question. Find the area of the trapezium PQRS with height PQ given in Fig. 12.3
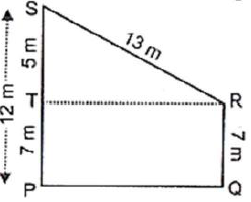
Answer. Draw RT ^ PS from the figure, it is clear that
ST = PS – PT
= 12 m – 7 m
= 5 m
Now, from right triangle RTS, we have
RS2 = RT2 + ST2
⇒ RT2 = RS2 – ST2 = (13)2 – 52
∴ RT2 = 169 − 25 = 144 ⇒ RT = + √144 = 12m
Now area of trapezium PQRS
= PS + QR × RT = 1/2 (12m + 7m) x 12
= 1/2 x 19m x 12m = 1/2 x 228m2 = 12m2
Question. The sides of a quadrilateral ABCD are 6 cm, 8 cm, 12 cm and 14 cm (taken in order) respectively, and the angle between the first two sides is a right angle. Find its area.
Answer. We have to find that the area of quadrilateral ABCD. ABC is a right triangle.
∴ By Pythagoras theorem, we have
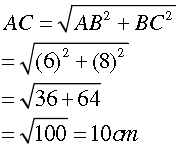
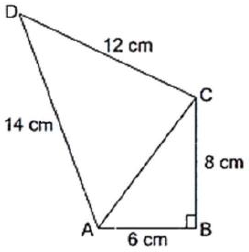
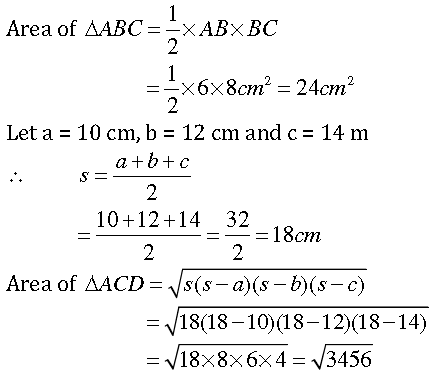
= 58.787cm (approx.)
∴ Area of quadrilateral ABCD
= Area of ΔABC + Area of ΔACD
= 24cm2 + 58.787cm2
= 82.787cm2 (approx.)
Question. A rhombus shaped sheet with perimeter 40 cm and one diagonal 12 cm, is painted on both sides at the rate of Rs 5 per m2. Find the cost of painting.
Answer. Perimeter of rhombus = 40 cm
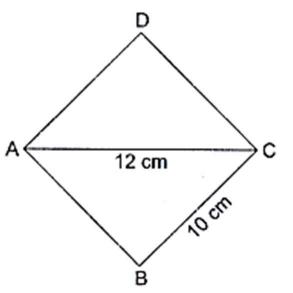
∴ 4 × side = 40
⇒ side = 40 / 4 = 10 cm
One diagonal = 12 cm
As rhombus is also a parallelogram, so it diagonal divide it into two congruent triangles of equal area.
∴ Area of rhombus = 2(Area of triangle with sides 10cm, 10cm and 12cm)
So, let a = 10 cm, b = 10 cm and c = 12 cm
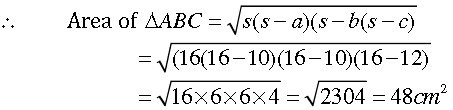
Now, area of rhombus ABCD = 2(area of ΔABC )
= 2 × 48 cm2 = 86 cm2.
Now, cost of painting both sides of rhombus shaped sheet ABCD
= Rs 2 × 5 × 96 = Rs 960
Question. How much paper of each shade is needed to make a kite given in Fig. 12.4, in which ABCD is a square with diagonal 44 cm.
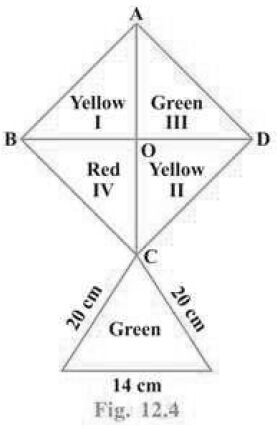
Answer. Each diagonal of square = 44 cm and as diagonal of a square bisect each other at right angles.
∴ Area of square ABCD
= 2(area of ΔABC)
= 2(1/2 x 44 22) = 2(44 x 11)
= 968 cm2.
∴ Paper of Red shade needed to make the kite
= 1/4(968cm2) = 242cm2
Paper of yellow shade needed to make the kite = (242 + 242) = 484 cm2.
Let us find the area of a triangle with sides 20 cm, 20 cm and 14 cm which is at the bottom of the square ABCD.
Now, semi-perimeter
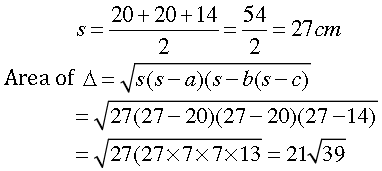
= 21 × 6.245 = 131.15cm
Paper of Green shade needed to make the kite
= (242 + 131.15) cm2 = 373.15 cm2.
Question. The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
Answer. Let the smaller side of the triangle be x cm. therefore, the second side will be (x + 4) cm, and third side is (2x – 6)cm.
Now, perimeter of triangle = x (x + 4) + (2x – 6) = (4x – 2)cm
Also, perimeter of triangle = 50 cm. 4x = 52; x = 52 ÷ 4 = 13
Therefore, the three sides are 13 cm, 17cm, 20cm
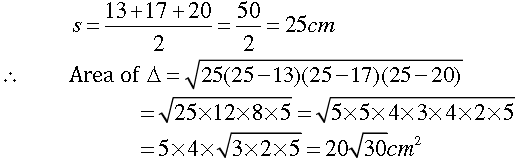
Question. The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
Answer. Area of trapezium = 1/2 × (Sum of the parallel side) × height
⇒ 475 = 1/2 x (x + x + 4) x 19cm
⇒ 2x + 4 = 950/19 = 50
⇒ 2x + 50 – 4 = 46, x = 46 ÷ 2 = 23
Hence, the length of two parallel sides are 23 cm and (23 + 4) cm i.e., 23 cm and 27 cm.
Question. A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
Answer. The length of the rectangular plot = 40 m
And the breath of the plot = 15 m.
As a minimum of 3 m wide space should be left in the front and back 2 m wide space each
of other side, so the largest area where the house can be constructed.
= [40 − 2(3)] [15− 2(2)] = 34 × 11 = 374m2
Question. The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the Fig. 12. 6. If the area of the trapezium PQCD is 5/6 th part of the area of the rectangle, find the lengths QC and PD.
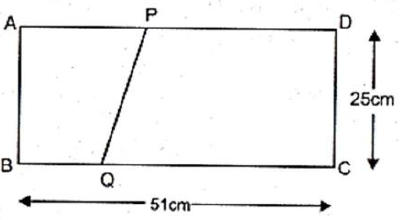
Answer. ABCD is a rectangle in which AB = 51 cm and BC = 25 cm.
Since parallel sides QC and PD are in the ratio 9:8, so let QC = 9 x and PD = 8x.
Now, are of trapezium PACD = 1/2 x (9x + 8x) x 25cm2
= 1/2 x 17x X 25
Area of rectangle ABCD = BC × CD = 51 × 25
It is given that area of trapezium PQCD = 5/6 × Area of rectangle ABCD.
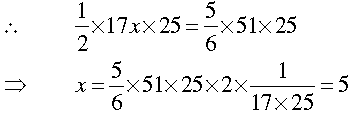
Hence, the length QC = 9x = 9 × 5 = 45 cm.
And the length PD = 8x = 8 × 5 = 40 cm.
Question. A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs4 to plough 1m2 of the field, find the total cost of ploughing the field.
Answer. The two-parallel side are AB = 90 cm and CD = 30 m. DM ⊥ AB
Now, MB = AB – AM = 90 m – 30 m = 60 m.
In right triangle DMB, we have
DM2 = DB2 – MB2 = (100)2 – (60)2
DM2 = 10,000 – 3600 = 6400
⇒ DM = + √6400 = 80m
∴ The area of the field ABDC which is trapezium in shape
= 1/2 × (Sum of the parallel sides) ×height
= 1/2 x (90 + 30) x 80m2
= 1/2 x 120 x 80 = 4800m2
Total cost of ploughing the field at the rate of Rs4 per m2 = Rs(4800 × 4) = Rs19,200.
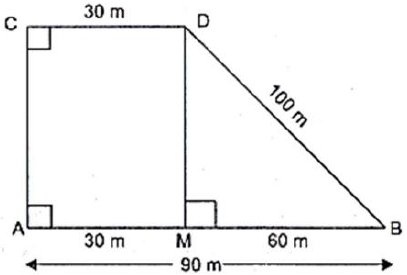
Question. In Fig. 12.5, Δ ABC has sides AB = 7.5 cm, AC = 6.5 cm and BC = 7 cm. On base BC a parallelogram DBCE of same area as that of Δ ABC is constructed. Find the height DF of the parallelogram.
Answer. Sides of triangle ABC are 7.5cm, 7cm and 6.5cm.
The semi-perimeter of ΔABC
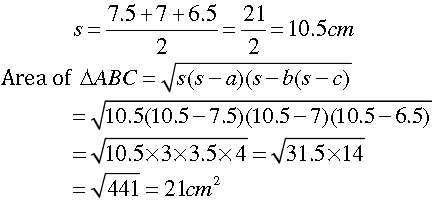
Now, as on base BC a parallelogram ΔBCE of same area of as that of ΔABC is constructed.
Therefore, area of ||gm ΔBCE = BC × DF
∴ BC × DF = 21cm2
⇒ 7 × DF = 21cm2
⇒ DF = 21cm2 ÷ 7cm = 3cm
Hence, the height DF of the parallelogram = 3cm.
Question. A design is made on a rectangular tile of dimensions 50 cm × 70 cm as shown in Fig. 12.7. The design shows 8 triangles, each of sides 26 cm, 17 cm and 25 cm. Find the total area of the design and the remaining area of the tile.
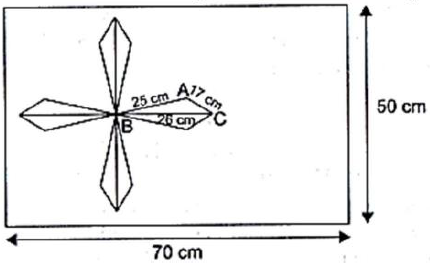
Answer. Given, the dimension of rectangular tile are 50 cm × 70 cm
∴ Area of rectangular tile = 50 × 70 = 3500 cm2.
The sides of a design of one triangle be a = 25 cm, b = cm and c = 26 cm.
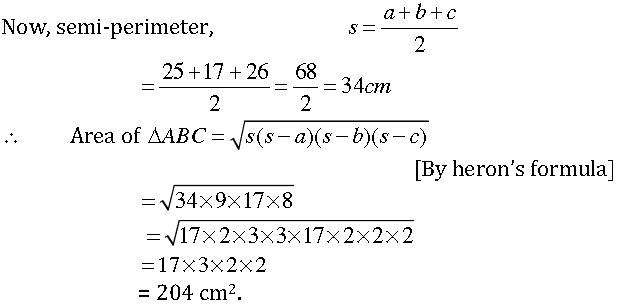
∴ Total area of eight triangles = 240 × 8 = 1632cm2
Now, area of the design = Total area of eight triangles
= 1632 cm2
Also, remaining area of the tile = Area of the rectangle – Area of the design
= 3500 cm2 – 1632 cm2
= 1868 cm2
Hence, the total area of the design is 1632 cm2 and the remaining area of the tile is 1868cm2.
Mathematics Herons Formula Worksheets for Class 9 as per CBSE NCERT pattern
Parents and students are welcome to download as many worksheets as they want as we have provided all free. As you can see we have covered all topics which are there in your Class 9 Mathematics Herons Formula book designed as per CBSE, NCERT and KVS syllabus and examination pattern. These test papers have been used in various schools and have helped students to practice and improve their grades in school and have also helped them to appear in other school level exams. You can take printout of these chapter wise test sheets having questions relating to each topic and practice them daily so that you can thoroughly understand each concept and get better marks. As Mathematics Herons Formula for Class 9 is a very scoring subject, if you download and do these questions and answers on daily basis, this will help you to become master in this subject.
Benefits of Free Heron’s Formula Class 9 Worksheet with Answers
- You can improve understanding of your concepts if you solve NCERT Class 9 Mathematics Herons Formula Worksheet,
- These CBSE Class 9 Mathematics Herons Formula worksheets can help you to understand the pattern of questions expected in Mathematics Herons Formula exams.
- All worksheets for Mathematics Herons Formula Class 9 for NCERT have been organized in a manner to allow easy download in PDF format
- Parents will be easily able to understand the worksheets and give them to kids to solve
- Will help you to quickly revise all chapters of Class 9 Mathematics Herons Formula textbook
- CBSE Class 9 Mathematics Herons Formula Workbook will surely help to improve knowledge of this subject
These Printable practice worksheets are available for free download for Class 9 Mathematics Herons Formula. As the teachers have done extensive research for all topics and have then made these worksheets for you so that you can use them for your benefit and have also provided to you for each chapter in your ebook. The Chapter wise question bank and revision worksheets can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 9 Mathematics Herons Formula Worksheets PDF.

You can download free worksheets for Class 9 Mathematics Herons Formula from https://www.worksheetsbag.com
You can get free PDF downloadable worksheets for Grade 9 Mathematics Herons Formula from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided worksheets for all subjects in Grade 9, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.worksheetsbag.com without any charge
Yes all test papers for Mathematics Herons Formula Class 9 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all worksheets.
https://www.worksheetsbag.com is the best portal to download all worksheets for all classes without any charges.