Linear Equations in Two Variables Class 9 Worksheet with Solutions have been designed as per the latest pattern for CBSE, NCERT and KVS for Grade 9. Students are always suggested to solve printable worksheets for Mathematics Linear Equations in two variables Grade 9 as they can be really helpful to clear their concepts and improve problem solving skills. We at worksheetsbag.com have provided here free PDF worksheets for students in standard 9 so that you can easily take print of these test sheets and use them daily for practice. All worksheets are easy to download and have been designed by teachers of Class 9 for benefit of students and is available for free download.
Mathematics Linear Equations In Two Variables Worksheets for Class 9
We have provided chapter-wise worksheets for class 9 Mathematics Linear Equations In Two Variables which the students can download in Pdf format for free. This is the best collection of Mathematics Linear Equations In Two Variables standard 9th worksheets with important questions and answers for each grade 9th Mathematics Linear Equations In Two Variables chapter so that the students are able to properly practice and gain more marks in Class 9 Mathematics Linear Equations In Two Variables class tests and exams.
Chapter-wise Class 9 Mathematics Linear Equations In Two Variables Worksheets Pdf Download
1. Linear Equations
2. Solution of a Linear Equation
3. Graph of a Linear Equation in Two Variables
4. Equations of Lines Parallel to x-axis and y-axis
• An equation of the form ax + by + c = 0 where a, b and c are real numbers such that a and b are not both zero is called a linear equation in two variables.
• A pair of values of x and y which satisfy the equation ax + by + c = 0 is called a solution of the equation.
• Graph: The graph of every linear equation in two variables is a straight line. Every point on the graph of a linear equation in two variables is two variables is a solution of the linear equation. Conversely, every solution of the linear equation is a point on the graph of the linear equation.
• A linear equation in two variables has infinitely many solutions.
• The graph of every linear equation in two variables is a straight line.
• y = 0 is the equation of x-axis and x = 0 is equation of y-axis.
• The graph of x = a is a straight line parallel to the y-axis.
• The graph of y = a is a straight line parallel to the x-axis.
• An equation of the type y = mx represent a line passing through the origin.
Question. If (2, 0) is a solution of the linear equation 2x+ 3y= k, then the value of k is
(a) 4
(b) 6
(c) 5
(d) 2
Answer
A
Question. The equation 2x+ 5y = 7 has a unique solution, if x, y are:
(a) Natural numbers
(b) Positive real numbers
(c) Real numbers
(d) Rational numbers
Answer
A
Question. The equation x= 7, in two variables, can be written as
(a) 1.x + 1.y = 7
(b) 1.x + 0.y = 7
(c) 0.x + 1.y = 7
(d) 0.x + 0.y = 7
Answer
B
Question. Any solution of the linear equation 2x + 0y + 9 = 0 in two variables is of the form:
(a) (-9/2,m)
(b) (n,-9/2)
(c) (0,-9/2)
(d) (-9,0)
Answer
A
Question. The graph of the linear equation 2x + 3y= 6 cuts the y-axis at the point
(a) (2, 0)
(b) (0, 3)
(c) (3, 0)
(d) (0, 2)
Answer
D
Question. Any point on the x-axis is of the form
(a) (x, y)
(b) (0, y)
(c) (x, 0)
(d) (x, x)
Answer
C
Question. The graph of the linear equation 2x+ 3 y= 6 is a line which meets the x-axis at the point
(a) (0, 2)
(b) (2, 0)
(c) (3, 0)
(d) (0, 3)
Answer
C
Question. Any point on the line y = x is of the form
(a) (a, a)
(b) (0, a)
(c) (a, 0)
(d) (a, – a)
Answer
A
Question. The linear equation 2x– 5 y= 7 has
(a) A unique solution
(b) Two solutions
(c) Infinitely many solutions
(d) No solution
Answer
C
Question. The equation of x-axis is of the form
(a) x = 0
(b) y = 0
(c) x + y = 0
(d) x = y
Answer
B
Question. If a linear equation has solutions (–2, 2), (0, 0) and (2, – 2), then it is of the form
(a) y – x = 0
(b) x + y = 0
(c) –2x + y = 0
(d) –x + 2y = 0
Answer
B
Question. The graph of y = 6 is a line
(a) parallel to x -axis at a distance 6 units from the origin
(b) parallel to y -axis at a distance 6 units from the origin
(c) making an intercept 6 on the x-axis.
(d) making an intercept 6 on both the axes.
Answer
A
Question. The positive solutions of the equation ax + by + c = 0 always lie in the
(a) 1st quadrant
(b) 2nd quadrant
(c) 3rd quadrant
(d) 4th quadrant
Answer
A
Question. x = 5, y= 2 is a solution of the linear equation
(a) x + 2y = 7
(b) 5x + 2y = 7
(c) x + y = 7
(d) 5x + y = 7
Answer
C
Question. The graph of the linear equation y = x passes through the point.
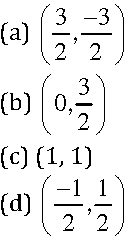
Answer
A
Question. The point of the form (a, a) always lies on:
(a) x-axis
(b) y-axis
(c) On the line y= x
(d) On the line x+ y = 0
Answer
C
Question. How many linear equations in x and y can be satisfied by x = 1 and y= 2?
(a) Only one
(b) Two
(c) Infinitely many
(d) Three
Answer
C
Question. The point of the form (a, –a) always lies on the line
(a) x = a
(b) y = –a
(c) y = x
(d) x + y = 0
Answer
D
Question. If we multiply or divide both sides of a linear equation with a non-zero number, then the solution of the linear equation:
(a) Changes
(b) Remains the same
(c) Changes in case of multiplication only
(d) Changes in case of division only
Answer
B
Question. Every point on the graph of a linear equation in two variables does not represent a solution of the linear equation.
Answer. As every point on the graph of linear equation in two variables represent a solution of the equation, so the given statement is false.
Question. The graph given below represents the linear equation x + y= 0.
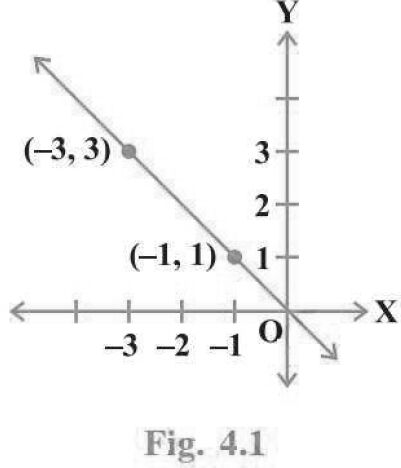
Answer. The given equation is x + y = 0, i.e., y = -x. Any point on the graph of y = – x, will have x and y coordinates of opposite signs. As the points (-1, 1) and (-3, 3) have x and y coordinates of opposite signs, so these points satisfy the given equation and the two points determine a unique line, hence the given statement is true.
Question. The graph given below represents the linear equation x = 3 (see Fig. 4.2).
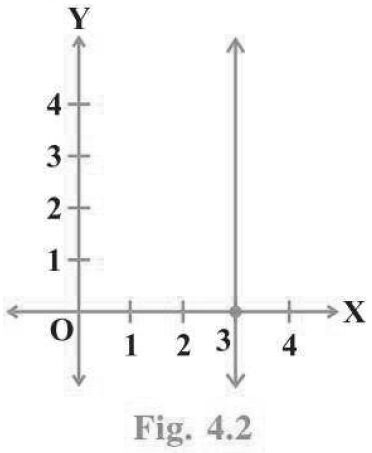
Answer. We know that the graph of the equation x = a is a line parallel to the y-axis and to the right of y-axis, if a > 0.
The given statement is true, since the graph is a line parallel to y-axis at a distance of 3 units to the right of it.
Question. The point (0, 3) lies on the graph of the linear equation 3x + 4y= 12.
Answer. Substituting x = 0 and y = 3 in the equation 3 (0) + 4(3) =12 ⇒ 12 =12, which is true.
The point (0, 3) satisfies the equation 3x + 4y = 12.
Hence, the given statement is true.
Question. The coordinates of points in the table:

Represent some of the solution of the equation x – y + 2 = 0.
Answer. The points (0, 2), (1, 3), (2, 4) and (4, 6) satisfy the given equation x – y + 2 = 0. Each of these points is the solution of the equation x – y + 2 = 0. But, the satisfy the given equation as 3 – (–5) + 2 = 0, i.e., 3 + 5 + 2 = 0 or 10 = 0, which is false.
Hence, the given statement is false, since the point (3, -5) does not satisfy the given equation.
Question. The graph of every linear equation in two variables need not be a line.
Answer. As the graph of a linear equation in two variables is always a line, so the given statement is false.
Question. Draw the graphs of linear equations y = x and y = – x on the same Cartesian plane. What do you observe?
Answer. Any point on the graph of y = x will have x and y coordinates same. The line passes through the points (0, 0), (1, 1) and (-1, -1).
Again, any point on the graph of y = -x will have x and y coordinates of opposite signs. The line passes through the points (1, -1) and (-1, 1). Also, (0, 0) satisfy y = -x.
The graph of linear equation y = x and y = – x on the same Cartesian plane is shown in the figure given below.
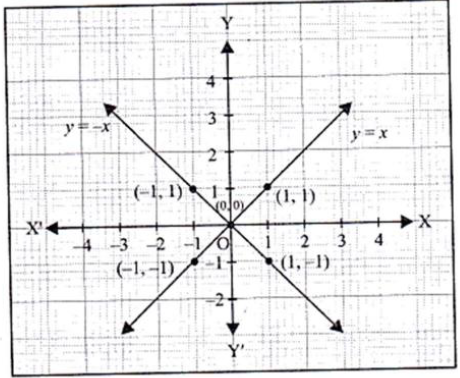
We observe that the graph of these equation passes through (0, 0).
Question. Determine the point on the graph of the linear equation 2x+ 5y= 19, whose ordinate is 1(1/2) times its abscissa.
Answer. Let the coordinate of the point be (2, 3).
Now, for x = 2 and y = 3.
2x + 5y = 2(2) + 5(3) = 4 +15 =19
Therefore, the point (2, 3) is a solution of the equation 2x + 5y =19.
Abscissa of the point is 2 and ordinate is 3.

Question. The graph of the linear equation x+ 2y= 7 passes through the point (0, 7).
Answer. Substituting x = 0 and y = 7 in the given equation x + y 2y = 7, we get 0 + 2(7) = 7 ⇒ 14 = 7, which is false.
The point (0, 7) does not satisfy the equation.
Hence, the given statement is false.
Question. Draw the graph of the equation represented by a straight line which is parallel to the x-axis and at a distance 3 units below it.
Answer. The graph of the equation y = – 3 is a line parallel to the axis and at a distance 3 units below it. So, graph of the equation y = – 3 is a line parallel to x-axis and passing through the point (0, -3) as shown in the figure given below:

Question. Find the solution of the linear equation x+ 2y = 8 which represents a point on
(i) x-axis (ii) y-axis
Answer. We know that the point which lies on x-axis has its ordinate 0.
Putting y = 0 in the equation x + 2y = 8, we get x + 2(0) = 8 ⇒ x = 8
A point which lies on y-axis has its abscissa 0.
Putting x = 0 in the equation x + 2y = 8, we get 0 + 2y = 8 ⇒ y = 4
Question. Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.
Answer. A linear equation such that each point on it graph has an ordinate 3 times its abscissa is y = 3x. 6. If the point (3, 4) lies on the graph of 3y = ax + 7, then find the value of a.
Answer. The point (3, 4) lies on the graph of 3y = ax + 7.
Substituting x = 3 and y = 4 in the given equation 3y = ax + 7,we get
∴ 3× 4 = a × 3 + 7
⇒ 12 = 3a + 7 ⇒ 3a = 5 ⇒ a = 5/3
Question. How many solution(s) of the equation 2x+ 1 = x– 3 are there on the:
(i) Number line
(ii) Cartesian plane?
Answer. (i) The number of solution(s) of the equation 2x + 1 = x – 3 which are on the number line is one.
2x +1 = x − 3 ⇒ 2x − x = −3 − 1 ⇒ x = −4
∴ x = −4 is the solution of the given equation.
(ii) The number of solution(s) of the equation 2x + 1 = x – 3 which are on the Cartesian plane are infinitely many solutions.
Question. For what value of c, the linear equation 2x+ cy = 8 has equal values of x and y for its solution.
Answer. The value of c for which the linear equation 2x + cy = 8 has equal values of x and y i.e., x = y for its solution is
2x + cy = 8 ⇒ 2x + cx = 8 [∵ y = x]
⇒ cx = 8 − 2x
∵ c = 8 – 2x/x, x ≠ 0
Question. Let y varies directly as x. If y = 12 when x = 4, then write a linear equation. What is the value of y when x = 5?
Answer. y varies of directly as x.
⇒ y ∝ x,
∴ y = kx
Substituting y = 12 when x = 4, we get
12 = k × 4 ⇒ k = 12 ÷ 4 = 3
Hence, the required equation is y = 3x.
The value of y when x = 5 is y = 3 × 5 =15.
Question. Show that the points A (1, 2), B (– 1, – 16) and C (0, – 7) lie on the graph of the linear equation y= 9 x – 7.
Answer. For A (1, 2), we have 2 = 9 (1) – 7 = 9 – 7 = 2
For B (–1, –16), we have –16 = 9(–1) – 7 = – 9 – 7 = – 16
For C (0, –7), we have – 7 = 9 (0) – 7 = 0 – 7 = – 7
We see that the line y = 9x – 7 is satisfied by the points A (1, 2), B (–1, –16) and C (0, –7).
Therefore, A (1, 2), B (–1, –16) and C (0, –7) are solutions of the linear equation y = 9x – 7 and therefore, lie on the graph of the linear equation y = 9x – 7.
Question. The linear equation that converts Fahrenheit (F) to Celsius (oC) is given by the relation: C = 5F – 160 / 9
(i) If the temperature is 86°F, what is the temperature in Celsius?
(ii) If the temperature is 35°C, what is the temperature in Fahrenheit?
(iii) If the temperature is 0°C what is the temperature in Fahrenheit and if the temperature is 0°F, what is the temperature in Celsius?
(iv) What is the numerical value of the temperature which is same in both the scales?
Answer. C = 5F – 160 / 9
(i) Putting F = 86o, we get C = 5 (86) – 160 / 9 = 430 – 160 / 9 = 270 / 9 = 30o
Hence, the temperature in Celsius is 30o C.
(ii) Putting C = 35o, we get 35o 5 (F) – 160 / 9 ⇒315o = 5F – 160
⇒ 5F = 315 +160 = 475
∴ F = 475 / 5 = 95o
Hence, the temperature in Fahrenheit is 95 F.
(iii) Putting C = 0o, we get
0 = 5F – 160 / 9 ⇒ 0 = 5 F – 160
⇒ 5F = 160
∴ F = 160 / 5 = 32o
Now, putting F = 0o, we get
C = 5F – 160 / 9 ⇒ C = 5(0) – 160 / 9 = – {160/9}o
If the temperature is 0o C, the temperature in Fahrenheit is 32o and if the temperature is 0F, then the temperature in Celsius is – {160/9}oC
(iv) Putting C = F, in the given relation, we get
F = 5F – 160 / 9 ⇒ 9F = 5F – 160
⇒ 4F = – 160
∴ F = – 160 / 4 = – 40o
Hence, the numerical value of the temperature which is same in both the scales is – 40.
The linear equation that converts Kelvin (x) to Fahrenheit (y) is given by the relation:
y = 9/5 (x – 273) + 32
Question. If the temperature of a liquid can be measured in Kelvin units as x° K or in Fahrenheit units as y° F, the relation between the two systems of measurement of temperature is given by the linear equation y = 9/5 (x – 273) + 32
(i) Find the temperature of the liquid in Fahrenheit if the temperature of the liquid is 313°K.
(ii) If the temperature is 158° F, then find the temperature in Kelvin.
Answer. y = 9/5 (x – 273) + 32
(i) When the temperature of the liquid is x = 313o K y = 9/5 (313 – 273) + 32 = 9/5 X 40 + 32 = 72o + 32o = 104oF
(ii) When the temperature of the liquid is y = 158o F
158 = 9/5 (x – 273) + 32 ⇒ 9/5 (x – 273) = 158 – 32
⇒ x − 273 = 126 × 5/6 = 70
⇒ x − 273 = 70 = 273 + 70 = 343o K
Question. The following observed values of x and y are thought to satisfy a linear equation.

Write the linear equation.
Draw the graph using the values of x, y given in the above table. At what points the graph of the linear equation
(i) cuts the x-axis (ii) cuts the y-axis
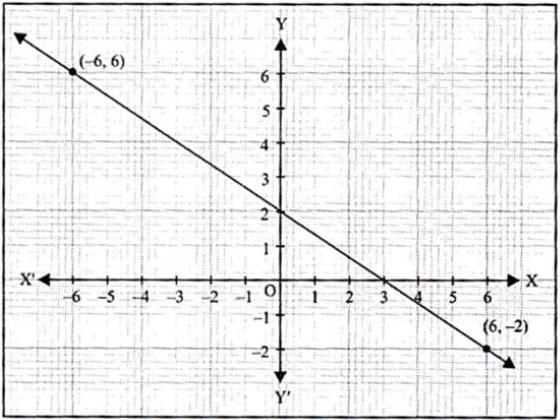
Answer. The linear equation is 2x + 3y = 6. Both the points (6, -2) and (-6, 6) satisfy the given linear equation. Plot the points (-6, 2) and (-6, 6) on a graph paper. Now join these two points and obtain a line. We see that the graph cuts the x-axis at (3, 0) and y-axis at (0, 2).
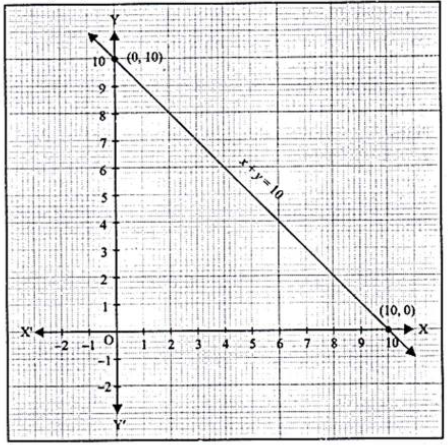
Question. Draw the graph of the linear equation whose solutions are represented by the points having the sum of coordinates as 10 units.
Answer. A linear equation whose solutions are represented by the points having the sum of coordinates as 10 units is x + y = 10.
When x = 0, y = 10 and when x = 10, y = 0.
Now, plot these two points (0, 10) and (10, 0) on a graph paper and join them to obtain a straight line.
The graph of x = y = 10 is a straight line as shown in the figure given below.
Question. Draw the graph of the linear equation 3x+ 4y= 6. At what points, the graph cuts the x-axis and the y-axis.
Answer. The solutions of the linear equation 3x + 4y = 6
Can be expressed in the form of a table as follows by writing the values of y below the corresponding value of x:

Now plot the points (2, 0), (-2, 3) and (0, 1.5) on a graph paper. Now, join the points and obtain a line.
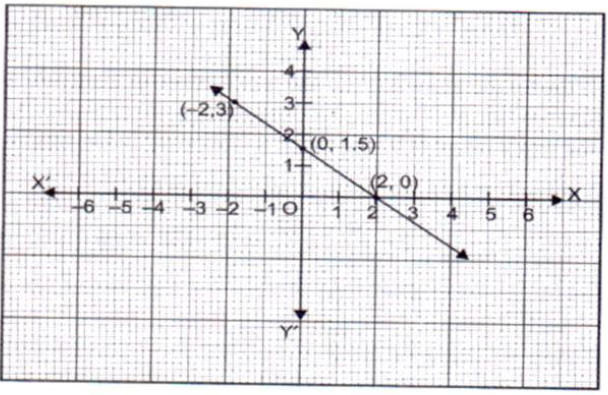
We see that the graph cuts the x-axis at (2, 0) and y-axis at (0, 1.5).
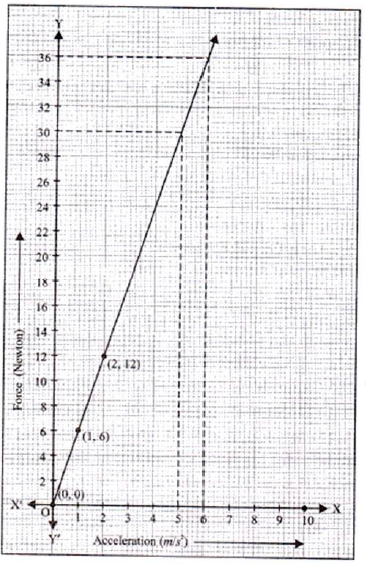
Question. The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as a linear equation in two variables and draw the graph of the same by taking the constant mass equal to 6 kg. Read from the graph, the force required when the acceleration produced is
(i) 5 m/sec2,
(ii) 6 m/sec2.
Answer. We have y ∝ x⇒ y = mx
Where y denotes the force, x denotes the acceleration and m denotes the constant mass.
Taking m = 6 kg, we get y = 6x
Now, we form a table as follows by writing the value of y below the corresponding value of x.

Plot the points (0, 0), (1, 6) and (2, 12) on a graph paper and join any two points and obtain a line.
Mathematics Linear Equations In Two Variables Worksheets for Class 9 as per CBSE NCERT pattern
Parents and students are welcome to download as many worksheets as they want as we have provided all free. As you can see we have covered all topics which are there in your Class 9 Mathematics Linear Equations in two variables book designed as per CBSE, NCERT and KVS syllabus and examination pattern. These test papers have been used in various schools and have helped students to practice and improve their grades in school and have also helped them to appear in other school level exams. You can take printout of these chapter wise test sheets having questions relating to each topic and practice them daily so that you can thoroughly understand each concept and get better marks. As Mathematics Linear Equations in two variables for Class 9 is a very scoring subject, if you download and do these questions and answers on daily basis, this will help you to become master in this subject.
Benefits of Free Linear Equations in Two Variables Class 9 Worksheet with Solutions
- You can improve understanding of your concepts if you solve NCERT Class 9 Mathematics Linear Equations in two variables Worksheets,
- These CBSE Class 9 Mathematics Linear Equations in two variables worksheets can help you to understand the pattern of questions expected in Mathematics Linear Equations in two variables exams.
- All worksheets for Mathematics Linear Equations in two variables Class 9 for NCERT have been organized in a manner to allow easy download in PDF format
- Parents will be easily able to understand the worksheets and give them to kids to solve
- Will help you to quickly revise all chapters of Class 9 Mathematics Linear Equations in two variables textbook
- CBSE Class 9 Mathematics Linear Equations in two variables Workbook will surely help to improve knowledge of this subject
These Printable practice worksheets are available for free download for Class 9 Mathematics Linear Equations in two variables. As the teachers have done extensive research for all topics and have then made these worksheets for you so that you can use them for your benefit and have also provided to you for each chapter in your ebook. The Chapter wise question bank and revision worksheets can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 9 Mathematics Linear Equations in two variables Worksheets PDF.

You can download free worksheets for Class 9 Mathematics Linear Equations in two variables from https://www.worksheetsbag.com
You can get free PDF downloadable worksheets for Grade 9 Mathematics Linear Equations in two variables from our website which has been developed by teachers after doing extensive research in each topic.
On our website we have provided worksheets for all subjects in Grade 9, all topic wise test sheets have been provided in a logical manner so that you can scroll through the topics and download the worksheet that you want.
You can easily get question banks, topic wise notes and questions and other useful study material from https://www.worksheetsbag.com without any charge
Yes all test papers for Mathematics Linear Equations in two variables Class 9 are available for free, no charge has been put so that the students can benefit from it. And offcourse all is available for download in PDF format and with a single click you can download all worksheets.
https://www.worksheetsbag.com is the best portal to download all worksheets for all classes without any charges.