Please refer to Binomial Theorem MCQ Questions Class 11 Mathematics below. These MCQ questions for Class 11 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Binomial Theorem will help you to prepare for the exams and get more marks.
Binomial Theorem MCQ Questions Class 11 Mathematics
Please see solved MCQ Questions for Binomial Theorem in Class 11 Mathematics. All questions and answers have been prepared by expert faculty of standard 11 based on the latest examination guidelines.
MCQ Questions Class 11 Mathematics Binomial Theorem
Question: Let[ x] denote the greatest integer less than or equal to x. If x = (√3+1)5 then [x ] x is equal to
(a) 75
(b) 50
(c) 76
(d) 152
Answer
D
Question: 1+1/3x+1.4/3.6 x2 +1·4·7/3·6·9 x3+… is equal to
(a) x
(b) (1+x)1/3
(c) (1-x)1/3
(d) (1-x)-1/3
Answer
D
Question: 1+2.1/3.2 +2.5/3.6(1/2)2 + 2·5 ·8/3·6·9·(1/2)3+…is equal to
(a) 21/3
(b) 31/4
(c) 41/3
(d) 31/3
Answer
C
Question: The coefficient of xn in the polynomial (x+nCo)(x+3nC1)(x+5nC2)…[x+(2n+1)nCn] ) is
(a) n· 2n
(b) n· 2n+1
(c) (n+1)2n
(d) n·2n+1
Answer
C
Question:

Answer
B
Question: The number of terms in the expansion of (a+ b+ c)n will be
(a) n + 1
(b) n + 3
(c) (n+1 ) (n+2)/2
(d) None of the above
Answer
C
Question: The coefficient of x7 in (1+3x- 2x3)10 ) is equal to
(a) 62640
(b) 26240
(c) 64620
(d) None of these
Answer
A
Question: Let Tn denotes the number of triangles which can be formed using the vertices of a regular polygon of n sides. If Tn +1-Tn=21, then n is equal to
(a) 5
(b) 7
(c) 6
(d) 4
Answer
B
Question:

Answer
B
Question: The value of x, for which the 6th term in the expansion of

Answer
C
Question: The coefficient of x2m+1 in the expansion of

(a) 3
(b) 2
(c) 1
(d) 0
Answer
C
Question:
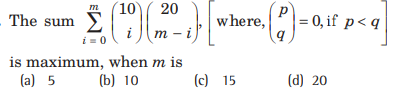
Answer
C
Question: Ifn-1Cr=(k2-3).n Cr+1,then k is belongs to
a) (-∞, -2]
(b) [2,∞)
(c) [- √3,√3]
(d) (√3 ,2]
Answer
D
Question:
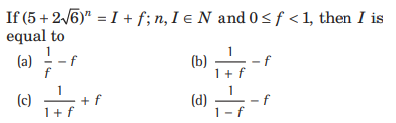
Answer
D
Question:

Answer
A
Question: If sum of the coefficients of the first, second and third terms of the expansion of [x2+1/x]m is 46, then the coefficient of the term that does not contain x is
(a) 84
(b) 92
(c) 98
(d) 106
Answer
A
Question: The number 101100 – is divisible by
(a) 100
(b) 1000
(c) 10000
(d) 100000
Answer
(a,b,c)
Question: The last digit of

(a) 4 C3
(b) 8C7
(c) 8
(d) 4
Answer
(a,d)
Question: Which of the following is/are correct?
(a) 10150-9950> 10050
(b) 10150– 10050> 99 50
(c) (1000) 1000> (1001)999
(d) (1001)999> (1000) 1000
Answer
(a,b,c)
The 2nd, 3rd and 4th terms in the expansion of( ) x a n + are 240, 720 and 1080, respectively.
Question: The value of (x-a) n can be
(a) 64
(b) -1
(c) -32
(d) None of these
Answer
B
Question: The sum of odd numbered terms is
(a) 1664
(b) 2376
(c) 1562
(d) 1486
Answer
C
Question: The value of least term in the expansion is
(a) 16
(b) 160
(c) 32
(d) 81
Answer
C
Assertion and Reason
Each of these questions contains two statements: Statement (Assertion) and Statement II(Reason).
Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c) and (d) given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true.
Question:
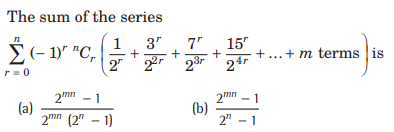
Answer
D
Question: Three consecutive binomial coefficients are given.
Statement I They cannot be in GP and HP.
Statement II They always are in AP.
Answer
B
Question: Statement I (√2+ 1)n can be expressed as of √N- √N -1) for all N > 1 and n is positive integer.
Statement II (√2- 1)n can be expressed as A+ B √2, where A and Bare integers and is positive integer.
Answer
B
Question: Statement I The number of terms in the expansion of
[x+1/x+1]n is 2n +1
Statement II

Answer
B
Question:

Answer
D
Question:
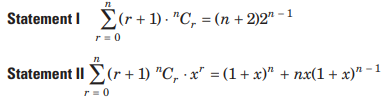
Answer
A
Question: Statement I The term independent of x in the expansion of (x+1/x+2)m is (4m)!/2m!)2·
Statement II The coefficient of x6 in the expansion of (1+x)n is nC6.
Answer
D
Question: Statement I Greatest term in the expansion of (1+x)12, when x=11/10 is 7th.

Answer
B
Question: Statement I If n is an odd prime, then the integral part of (√5+2)n-2n+1 is divisible by 2n
Statement II If n is prime, then nC1,nC2,…nCn-1 must be divisible by n.
Answer
A
Question:

Answer
A


