Please refer to Probability MCQ Questions Class 12 Mathematics below. These MCQ questions for Class 12 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Probability will help you to prepare for the exams and get more marks.
Probability MCQ Questions Class 12 Mathematics
Please see solved MCQ Questions for Probability in Class 12 Mathematics. All questions and answers have been prepared by expert faculty of standard 12 based on the latest examination guidelines.
MCQ Questions Class 12 Mathematics Probability
Question. If E1 and E2 are two events such that P(E1) = 1/4, P(E2/E1) = 1/2 and P(E1/ E2) = 1/4, then choose the incorrect statement
(a) E1 and E2 are independent
(b) E1 and E2 are exhaustive
(c) E2 is twice as likely to occur as E1
(d) Probabilities of the events E1 ∩ E2 , E1 and E2 are in G.P.
Answer
B
Question. If the mean and variance of a binomial variate x are respectively 35/6 and 35/36 , then the probability of x > 6 is :
(a) 1/62
(b) 57/67
(c) 1/76
(d) 1/67 + 1/67
Answer
B
Question. If P (A) = 1/2 , P (B) = 0, then P (A/B) is
(a) 0
(b) 1/2
(c) not defined
(d) 1
Answer
C
Question. The probability of safe arrival of one ship out of five is (1/5). The probability of safe arrival of atleast 3 ship is:
(a) 3/52
(b) 1/31
(c) 184/3125
(d) 181/3125
Answer
D
Question. In a hostel, 60% of the students read Hindi newspaper, 40% read English newspaper and 20% read both hindi and English news papers. A student is selected at random. Then, match the terms of column I with their respective values in column II.

Codes
A B C
(a) 3 1 2
(b) 1 2 3
(c) 2 3 1
(d) 3 2 1
Answer
A
Question. In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is :
(a) 10–1
(b) (1/2)5
(c) (9/10)5
(d) 9/10
Answer
C
Question. In a college, 30% students fail in physics, 25% fail in Mathematics and 10% fail in both. One student is chosen at random. The probability that she fails in Physics, if she has failed in mathematics, is
(a) 1/10
(b) 2/5
(c) 9/20
(d) 1/3
Answer
B
Question. An urn contains five balls. Two balls are drawn and found to be white. The probability that all the balls are white is
(a) 1/10
(b) 3/10
(c) 3/5
(d) 1/2
Answer
D
Question. The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Then, match the probability that out of 5 such bulbs will fuse after 150 days of use in column I with their respective values in column II.
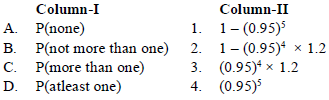
Codes
A B C D
(a) 2 4 1 3
(b) 4 3 2 1
(c) 4 3 1 2
(d) 4 1 3 2
Answer
B
Question. A bag contains 12 white pearls and 18 black pearls. Two pearls are drawn in succession without replacement. The probability that the first pearl is white and the second is black, is
(a) 32/145
(b) 28/143
(c) 36/145
(d) 36/143
Answer
C
Question. It is given that the events A and B are such that P (A)= 1/4 , P (A | B) = 1/2 and P (B | A) = 2/3. Then P(B) is
(a) 1/6
(b) 1/3
(c) 2/3
(d) 1/2
Answer
B
Question. Two events E and F are independent. If P(E) = 0.3, P(E ∪ F) = 0.5, then P(E | F) – P(F | E) equals
(a) 2/7
(b) 3/35
(c) 1/70
(d) 1/7
Answer
C
Question. The random variable X has the following probability distribution
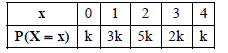
Then the value of P(X ≥ 2) is
(a) 1/3
(b) 2/3
(c) 3/4
(d) 1/4
Answer
B
Question. If A and B are independent events, then which of the following is not true ?
(a) P(A/B) = P(A)
(b) P(B/A) = P(B)
(c) P(A/B) = P(B/A)
(d) None of these
Answer
C
Question. One ticket is selected at random from 50 tickets numbered 00,01,02,…,49. Then the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals
(a) 1/7
(b) 5/14
(c) 1/50
(d) 1/14
Answer
D
Question. A box contains 20 identical balls of which 10 are blue and 10 are green. The balls are drawn at random from the box one at a time with replacement. The probability that a blue ball is drawn 4th time on the 7th draw is
(a) 27/32
(b) 5/64
(c) 5/32
(d) 1/2
Answer
C
Question. A drunken man takes a step forward with probability 0.4 and backwards with probability 0.6. Find the probability that at the end of eleven steps, he is one step away from the starting point.
(a) 24 × (0.36)6
(b) 462 × (0.24)6
(c) 24 × (0.36)5
(d) 462 × (0.24)5
Answer
D
Question. If A and B are 2 events such that P(A) > 0 and P(B) ≠ 1,
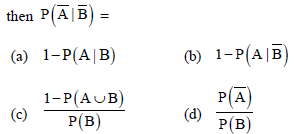
Answer
B
Question. Five defective mangoes are accidently mixed with 15 good ones. Four mangoes are drawn at random from this lot. Then the probability distribution of the number of defective mangoes is:

Answer
C
Question. If E and F are events such that 0 < P(F) < 1, then
(a) P(E | F) + P(E¯ | F) = 1
(b) P(E | F) + P(E | F¯) = 1
(c) P(E¯ | F) + P(E | F¯) = 1
(d) P(E | F¯) + P(E¯ | F¯) = 0
Answer
A
Question. Let X denote the number of hours you study during a randomly selected school day. The probability that X can take the values x, has the following form, where k is some unknown constant.
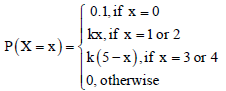
Then, match the terms of column I with their respective values in column II.
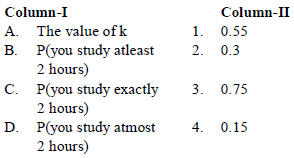
Codes
A B C D
(a) 1 4 3 2
(b) 4 3 1 2
(c) 4 2 3 1
(d) 4 3 2 1
Answer
D
Question. In a binomial distribution, mean is 3 and standard deviation is 3/2 , then the probability function is
(a) (3/4 + 1/4)12
(b) (1/4 + 3/4)12
(c) (1/4 + 3/4)9
(d) (3/4 + 1/4)9
Answer
A
Question. One hundred identical coins, each with probability p of showing up heads, are tossed. If 0 < p < 1 and the probability of heads showing on 50 coins is equal to that of heads showing on 51 coins. The value of p is
(a) 1/2
(b) 49/101
(c) 50/101
(d) 51/101
Answer
D
Question. Consider the following statement:
“The mean of a binomial distribution is 3 and variance is 4.” Which of the following is correct regarding this statement?
(a) It is always true
(b) It is sometimes true
(c) It is never true
(d) No conclusion can be drawn
Answer
C
Question. The random variable X has the following probability distribution:

Then, its mean is
(a) – 0.2
(b) 0.2
(c) – 0.4
(d) 0.4
Answer
A
Question. For a biased dice, the probability for the different faces to turn up are

The dice is tossed and it is told that either the face 1 or face 2 has shown up, then the probability that it is face 1, is
(a) 16/21
(b) 1/10
(c) 5/16
(d) 5/21
Answer
D
Question. Two dice are tossed 6 times. Then the probability that 7 will show an exactly four of the tosses is:
(a) 225/18442
(b) 116/20003
(c) 125/15552
(d) 117/17442
Answer
C
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C D E
(a) 1 2,3 4 5
(b) 1,2 3 5 4
(c) 2 3,4 1 5
(d) 3,4 2 5 1
Answer
D
Question. A die is thrown again and again until three sixes are obtained. The probability of obtaining third six in the sixth throw of the die, is
(a) 625/23329
(b) 621/25329
(c) 625/23328
(d) 620/23328
Answer
C
Question. Examples of some random variables are given below :
1. Number of sons among the children of parents with five children.
2. Number of sundays in some randomly selected months with 30 days.
3. Number of apples in some 3 kg packets, purchased from a retail shop.
Which of the above is expected to follow binomial distribution?
(a) Variable 1
(b) Variable 2
(c) Variable 3
(d) None of these
Answer
B
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C D
(a) 3 4 1 2
(b) 3 1 2 4
(c) 1 3 4 2
(d) 4 3 1 2
Answer
A
Question. Girl students constitute 10% of I year and 5% of II year at Roorkee University. During summer holidays 70% of the I year and 30% of II year students are given a project. The girls take turns on duty in canteen. The chance that I year girl student is on duty in a randomly selected day is
(a) 3/17
(b) 14/17
(c) 3/10
(d) 7/10
Answer
B
Question. In a binomial distribution, the mean is 4 and variance is 3. Then its mode is :
(a) 4
(b) 5
(c) 6
(d) 7
Answer
A
Question. By examining the chest X-ray, the probability that TB is detected when a person is actually suffering is 0.99. The probability of an healthy person diagnosed to have TB is 0.001. In a certain city, 1 in 1000 people suffers from TB, A person is selected at random and is diagnosed to have TB. Then, the probability that the person actually has TB is
(a) 110/221
(b) 2/223
(c) 110/223
(d) 1/221
Answer
A
Question. If A and B be two events such that P(A) = 0.6, P(B) = 0.2 and P(A/B) = 0.5, then P(A’ / B’) is equal to
(a) 1/10
(b) 3/10
(c) 3/8
(d) 6/7
Answer
C
STATEMENT TYPE QUESTIONS
Question. Consider the following statements
Statement I: An experiment succeeds twice as often as it fails. Then, the probability that in the next six trials, there will be atleast 4 successes is 31/9 (2/3)4
Statement II: The number of times must a man toss a fair coin so that the probability of having atleast one head is more than 90% is 4 or more than 4.
(a) Statement I is true
(b) Statement II is true
(c) Both statements are true
(d) Both statements are false
Answer
C
Question. I. Independent events and mutually exclusive events have one and the same meaning.
II If E1, E2,….En represent partition of a sample space then more than one of them can occur simultaneously.
(a) Only I is correct
(b) Only II is correct
(c) Both I and II are correct
(d) Both I and II are incorrect
Answer
D
Question. I. Partition of a sample space is unique.
II If n events represent position of a sample space then it is not necessary for them to be pairwise disjoint.
(a) Only I is correct
(b) Only II is correct
(c) Both I and II are correct
(d) Both I and II are incorrect
Answer
D
Question. A fair coin is tossed two times
I The first and second tosses are independent of each other.
II The sample space for the experiment is S = {HH, HT, TH, TT}
III Getting head in both the tosses is a sure event.
(a) Only I is correct
(b) Only I and II are correct
(c) All are correct
(d) Only III is correct
Answer
B
Question. I. Bernoulli’s trials of a random experiment can be infinite in number.
II The appearance of 50 students in a test that whether they pass or fail can be considered as 50 Bernoulli trials
III The 5 trials of drawing balls from a bag containing 8 white and 12 black balls with replacement can be considered as Bernoulli’s trials.
(a) Only I and II are correct
(b) Only II and III are correct
(c) Only III is correct
(d) All are correct
Answer
C


