Students should refer to Worksheets Class 12 Mathematics Determinants Chapter 4 provided below with important questions and answers. These important questions with solutions for Chapter 4 Determinants have been prepared by expert teachers for Class 12 Mathematics based on the expected pattern of questions in the class 12 exams. We have provided Worksheets for Class 12 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Determinants Worksheets Class 12 Mathematics
Question. Let M and N be two 3×3 non-singular skew-symmetric matrices such that MN = NM. If PT denotes the transpose of P, then M2 N2 (MT N)-1 (MN−1) is equal to:
(a) M2
(b) –N2
(c) –M2
(d) MN
Answer
C
Question. Let ω be a complex cube root of unity with ω ≠ 1 and P = [pij] be a n × n matrix with . Pe =ωi+j Then, p2 ≠ 0 when n is equal to:
(a) 57
(b) 55
(c) 58
(d) 56
Answer
B,C,D
Question. If the ad-joint of a 3 × 3 matrix

then the possible value(s) of the determinant of P is/are:
(a) –2
(b) –1
(c) 1
(d) 2
Answer
A,D
Question. Let M and N be two 3×3 matrices such that MN = NM.
Further, if M ≠ N2 and M2 = N4 , then:
(a) determinant of (M2 + MN2) is 0
(b) there is a 3×3 non-zero matrix U such that (M2 + MN2) U is zero matrix
(c) determinant of (M2 + MN2)≥1
(d) for a 3×3 matrix U, if (M2 + MN2) U equals the zero matrix, then U is the zero matrix.
Answer
A,B
Question. If the system of equations x + λy + 2 = 0, λx + y – 2 = 0, λx + λy + 3 = 0 is consistent, then
(a) λ = ±1
(b) λ = ± 2
(c) λ = 1, – 2
(d) λ = –1, 2
Answer
A
Question.
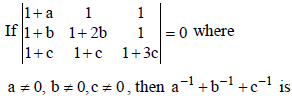
(a) 4
(b) –3
(c) –2
(d) –1
Answer
B
Question. If x, y, z are all distinct and

then the value of xyz is
(a) –2
(b) –1
(c) –3
(d) None of these
Answer
B
Question. If x ≠ y ≠ z and
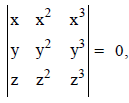
then xyz is equal to:
(a) 1
(b) – 1
(c) 0
(d) x + y + z
Answer
C
Question. The system of simultaneous linear equations kx + 2y – z = 1, (k – 1) y – 2z = 2 and (k + 2) z = 3 have a unique solution if k equals:
(a) – 1
(b) – 2
(c) 0
(d) 1
Answer
A
Question.
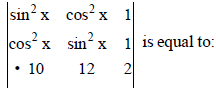
(a) 0
(b) 12 cos2 x – 10 sin2 x
(c) 12 cos2 x – 10 sin2 x – 2
(d) 10 sin 2x
Answer
A
Question.
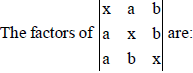
(a) x – a, x – b and x + a + b
(b) x + a, x + b and x + a + b
(c) x + a, x + b and x – a – b
(d) x – a, x – b and x – a – b
Answer
A
Question. If a–1 + b–1 + c–1 = 0 such that
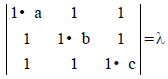
then the value of λ is :
(a) 0
(b) – abc
(c) abc
(d) None of these
Answer
C
Question. If any two rows (or columns) of a determinant are identical (all corresponding elements are same), then the value of determinant is
(a) 1
(b) –1
(c) 0
(d) 2
Answer
C
Question. If A and B are two square matrices such that B = – A–1 BA, then (A + B)2 =
(a) 0
(b) A2 + B2
(c) A2 + 2 AB + B2
(d) A + B
Answer
B
Question. If a square matrix satisfies the relation A2 + A – I = 0 then A–1:
(a) exists and equals I + A
(b) exists and equals I – A
(c) exists and equals A2
(d) None of these
Answer
A
Question.
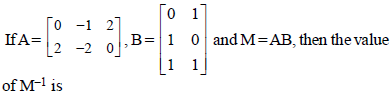
Answer
B
Question. If I3 is the identity matrix of order 3, then I3–1 is
(a) 0
(b) 3I3
(c) I3
(d) Does not exist
Answer
C
Question. The equations 2x + 3y + 4 = 0; 3x + 4y + 6 = 0 and 4x + 5y + 8 = 0 are
(a) consistent with unique solution
(b) inconsistent
(c) consistent with infinitely many solutions
(d) None of the above
Answer
A
Question. The value of x obtained from the equation
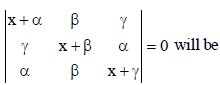
(a) 0 and –(α + β +γ)
(b) 0 and α +β + γ
(c) 1 and (α – β – γ)
(d) 0 and α2 + β2 + γ2
Answer
A
Question.
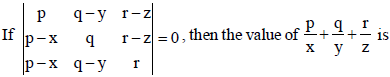
(a) 0
(b) 1
(c) 2
(d) 4pqr
Answer
C
Question.
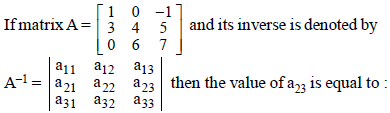
(a) 21/20
(b) 1/5
(c) – 2/5
(d) 2/5
Answer
C
Question.
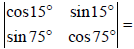
(a) 0
(b) 5
(c) 3
(d) 7
Answer
A
Question. The maximum value of

(a) 1/2
(b) √3/2
(c) √2
(d) 2√3/4
Answer
A
Question. If B is a non-singular matrix and A is a square matrix, then det (B–1 AB) is equal to
(a) det (A–1)
(b) det (B–1)
(c) det (A)
(d) det (B)
Answer
C
Question.
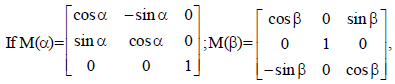
then value of [M(α) M (β)]–1 is
(a) M(β).M(α)
(b) M(–α).M(β)
(c) M(–β)M(α)
(d) M(–β)M(–α)
Answer
D
STATEMENT TYPE QUESTIONS
Question. Consider the following statements
I. Matrix cannot be reduced to a number.
II. Determinant can be reduced to a number.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
C
Question. Consider the following statements
I. | A | is also called modulus of square matrix A.
II. Every matrix has determinant.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
D
Question. Consider the following statements
I. If any two rows (or columns) of a determinant are interchanged, then sign of determinant changes.
II. If any two rows (or columns) of a determinant are interchanged, then the value of the determinant
remains same.
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
A
Question. Consider the following statements
I. To every rectangular matrix A = [aij] of order n, we can associate a number (real or complex) called determinant of A.
II. Determinant is a function which associates each square matrix with a unique number (real or complex).
(a) Only I is true
(b) Only II is true
(c) Both I and II are true
(d) Neither I nor II is true
Answer
B
ASSERTION – REASON TYPE QUESTIONS
Note: Read the Assertion (A) and Reason (R) carefully to mark the correct option out of the options given below:
(a) If both assertion and reason are true and the reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If the assertion and reason both are false.
e. If assertion is false but reason is true.
Question. Let

Assertion: A(π /3)3 = −I
Reason: R A(θ )A(ϕ ) = A(θ +ϕ )
Answer
A
Question. Let a ≠ 0, p ≠ 0 and
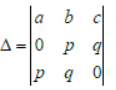
Assertion: If the equations ax2 + bx + c = 0 and px + q = 0 have a common root, then △ = 0.
Reason: If △ = 0 then the equations ax2 + bx + c = 0 and px + q = 0 have a common root.
Answer
B
Question. Assertion:

is a purely imaginary number.
Reason: | z |=|z̅| for each complex number z.
Answer
A
Question. Let

Assertion: If X ′AX = O for each X, then A must be a skew-symmetric matrix.
Reason: If A is symmetric and X ′AX = O for each X, then A = O
Answer
B
Question. Suppose x > 0, y > 0, z > 0 and

Assertion: △(8, 27, 125) = 0
Reason:

Answer
B
Question. Assertion: If A and B are two 3×3 matrices such that AB =O , then A = O or B = O.
Reason: If A, B and X are three 3×3 matrices such that AX = B,| A| ≠ 0, then 1 X A (b)
Answer
D
Question. Assertion: If
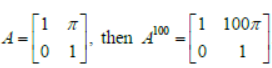
Reason: If B is a 2 × 2 matrix such that B2 = O, then (I + B)n = I + nB for each n∈N.
Answer
A
Question. Assertion: As

satisfies the equation x3 − 5×2 + 7x − 3 = 0, then A is invertible.
Reason: If a square matrix A satises the equation a0xn + a1xn-1 +….+ an-1x+an = and an ≠ 0 then A is invertible.
Answer
A
Question. Assertion: If a, b, c are in (a)P. the system of equations
3x + 4y + 5z = a . . .(i)
4x + 5y + 6z = b . . .(ii)
5x + 6y + 7z = c . . .(iii)
is consistent.
Reason: If |A| ≠ 0, the system of equations AX =B is consistent.
Answer
B
Paragraph
Let △ ≠ 0 and △e denotes the determinants of cofactors, then △e = △n–1, where n(>0) is the order of △.
Question. If a, b, c are the roots of the equations x2 − px2 + r = 0, then the value of
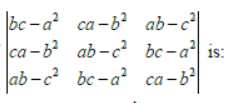
(a) p2
(b) p4
(c) p6
(d) p9
Answer
C
Question. If l1 ,m1 ,n1 ;l2 ,m2 ,n2 ;l3 ,m3 ,n3 are real quantities satisfying the six relations
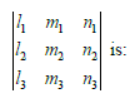
(a) 0
(b) ±1
(c) ±2
(d) ±3
Answer
B
Question. If a,b,c are the roots of the equation x3 − 3×2 + 3x + 7 = 0, then the value of

(a) 9
(b) 27
(c) 81
(d) 0
Answer
D
Question. If a2 + b2 + c2 = λ , then the value of
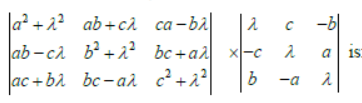
(a) 8λ6
(b) 27λ9
(c) 8λ9
(d) 27λ6
Answer
C
Question. Suppose a,b,c∈R ,a = b + c > 0, A = bc – a2 , B = ca – b2, and
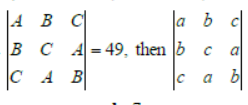
(a) – 7
(b) 7
(c) – 2401
(d) 2401
Answer
B
Match the Column
Question. Match the entries of Column I and Column II

(a) A→ 3; B→ 1; C→ 2; D→ 5, E→ 4
(b) A→ 3; B→ 1; C→ 2; D→ 4, E→ 5
(c) A→ 1; B→ 3; C→ 2; D→ 5, E→ 4
(d) A→ 3; B→ 1; C→ 5; D→ 2, E→ 4
Answer
A
Question. Match the following

(a) A→1; B→1; C→1; D→1
(b) A→3; B→1; C→4; D→2
(c) A→3; B→1; C→2; D→4
(d) A→1; B→3; C→4; D→2
Answer
A
Question. Consider the following linear equations


(a) A→2; B→4; C→3; D→1
(b) A→1; B→3; C→4; D→2
(c) A→2; B→3; C→4; D→1
(d) A→2; B→3; C→1; D→4
Answer
C
Question. Consider the following linear equations ax + by + cz = 0, bx + cy + az = 0, cx + ay + bz = 0:

(a) A→3; B→1; C→4; D→2
(b) A→3; B→1; C→4; D→2
(c) A→3; B→2; C→1; D→4
(d) A→3; B→1; C→4; D→2
Answer
C
Question. Let k be a positive real number an d let
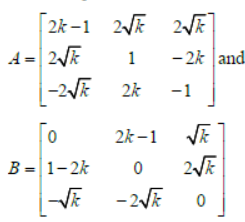
If det(adjA) + det(adjB)=106 then [k] is equal to ……
[Note: adjM denotes the adjoint of a square matrix M and [k] denotes the largest integer less than or equal to k].
Answer
4
Question. Let M be a 3 × 3 matrix satisfying

Then, the sum of the diagonal entries of M is:
Answer
9
Question. If
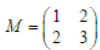
and M2 –λM – I2 = O, then 6λmust be:
Answer
1296
Question. If
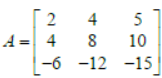
the rank of A is:
Answer
1
Question. Let

Answer
896