Students should refer to Worksheets Class 10 Mathematics Quadratic Equation Chapter 4 provided below with important questions and answers. These important questions with solutions for Chapter 4 Quadratic Equation have been prepared by expert teachers for Class 10 Mathematics based on the expected pattern of questions in the Class 10 exams. We have provided Worksheets for Class 10 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Quadratic Equation Worksheets Class 10 Mathematics
VERY SHORT ANSWER TYPE QUESTIONS
Question. If 1/2 is a root of x2 + px – 5/4 = 0 then value of p is
(a) 2
(b) –2
(c) 1/4
(d) 1/2
Ans. (a) 2
Question. Which of the following is not a Quadratic Equation?
(a) 2(x – 1)2 = 4x2 – 2x + 1
(b) 3x – x2 = x2 + 6
(c) (√3x+√2)2 = 2x2 – 5x
(d) (x2 + 2x)2 = x4 + 3 + 4x2
Ans. (d) (x2 + 2x)2 = x4 + 3 + 4x2
Question. Roots of Quadratic equation x2 – 7x = 0 will be
(a) 7
(b) 0, –7
(c) 0, 5
(d) 0, 7
Ans. (d) 0, 7
Question. The value of k for which the roots of qaudratic equations x2 + 4x + k = 0 are real is ______ .
Ans. k ≤ 4 [D ≥ 0 ⇒ 16 – 4 k ≥ 0 ⇒ 16 ≥ 4k ⇒ 4 ≥ k]
Question. If px2 + qx + r = 0 has equal roots then value of r will be ______ .
Ans. [r = q2/4p (D = 0 ⇒ q2 – 4pr = 0)]
Question. If in a quadratic equation ax2 + bx + c = 0, value of a is zero then it become a _____ equation.
Ans. Linear equation (x = 0 ⇒ ax2 + bx + c = 0 reduces to bx + c = 0)
Question. 0.3 is a root of x2 – 0.9 = 0. True or False
Ans. False ((0.3)2 – 0.9 = 0.09 – 0.9 ≠ 0)
Question. Every quadratic equation has atleast one real roots. True or False
Ans. False (A quadratic equation has atmost two real root).
SHORT ANSWER TYPE QUESTIONS-I
Question. Solve for x by factorisation 3x2 – 2√6 x + 2 = 0
Ans. x = √2/3, x = √2/3
Question. If – 5 is a root of the quadratic equation 2x2 + px – 15 = 0 and the quadratic equation p(x2 + x) + k = 0 has equal roots find the value of k.
Ans. 2(– 5)2 + p(– 5) – 15 = 0 ⇒ p = 7
∴ 7x2 + 7x + k = 0, D = 49 – 28 k = 0
⇒ k = 49/28 = 7/4
Question. If the Quadratic equation px2 – 2 5 px + 15 = 0 (p ≠ 0) has two equal roots then find the value of p.
Ans. D = 0
20p2 – 60p = 0, p ≠ 0
20p (p – 3) = 0
p = 3
Question. Solve for x by factorisation 3√5x2 + 25x + 10√5 = 0
Ans. x = -√5, x = (-2√5)/3
Question. The sides of two squares are x cm and (x + 4) cm. The sum of their areas is 656 cm2 Find the sides of these two squares.
Ans. x2 + (x + 4)2 = 656
x2 + 4x – 320 = 0
D = 1296 x = (-4±√1296)/2 = (-14+36)/2, (-4-36)/2
x = 32/2 = 16, (rejecting –ve value)
Sides are 16 cm, 20 cm
Question. Solve for x by factorisation 2x2 + ax – a2 = 0
Ans. x = a/2, x = -a
Question. Find K if the difference of roots of the quadratic equation x2 – 5x + (3k – 3) = 0 is 11.
Ans.

SHORT ANSWER TYPE QUESTIONS-II
Question. If the roots of the quadratic equation (p + 1)x2 – 6(p + 1) x + 3(p + 9) = 0 are equal find p and then find the roots of this quadratic equation.
Ans. D = 0
∴ p2 – 2p = 0 ; p = -1, 3
rejecting p = –1,
∴ Answer is p = 3
Question. Solve for x
4x2 + 4bx – (a2 – b2) = 0
Ans.

Question. Find the positive value of k for which the quadratic equation x2 + kx + 64 = 0 and the quadratic equation x2 – 8x + k = 0 both will have real roots.
Ans.

Question. Solve for x
1/(2a + b + 2x) = 1/2a + 1/b + 1/2x
2a + b + 2x ≠ 0, a, b, x ≠ 0
Ans.
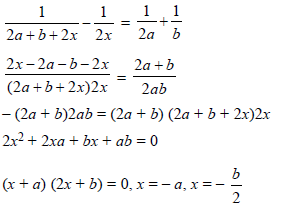
Question. Solve for x
1/(x-1) – 1/(x+5) = 6/7, x ≠ 1,5
Ans. Take LCM to get x2 + 4x – 12 = 0
x = 2, – 6
Question. Solve for x
4x2 – 2(a2 + b2) x + a2b2 = 0
Ans.

Question. Solve for x
x2 + 5√5x – 70 = 0
Ans.
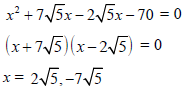
Question. Solve for x
2x/(x-3) + 1/(2x+3) + (3x+9)/((x-3)(2x+3)) = 0, x ≠ 3, -3/2
Ans. Take LCM to get 2x2 + 5x + 3 = 0, x = – 1, x ≠ -3/2. (given)
Question. Solve for x
1/(x+4) – 1/(x-7) = 11/30, x ≠ -4, 7
Ans. Take LCM to get x2 – 3x + 2 = 0
Solve to get x = 1, x = 2
Question. Solve for x
4x2 – 4a2x + a4 – b4 = 0
Ans.
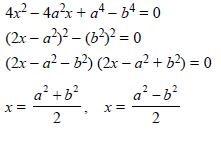
Question. Solve for x
3(7x+1/5x-3) – 4(5x-3/7x+1) = 11, x ≠ 3/5, -1/7
Ans.

LONG ANSWER TYPE QUESTIONS
Question. Sum of areas of two squares is 400 cm2. If the difference of their perimeter is 16 cm. Find the side of each square.
Ans. x2 + y2 = 400 …(1)
4x – 4y = 16 ⇒ x – y = 4 …(2)
y – x = 4 …(3)
Solve (1) and (2) to get x = 16, x = –12 (rejected)
Solve (1) and (3) to get x = 12, x = –16 (rejected)
x = 16 m, y = 12 m from (1) and (2)
x = 12 m, y = 16 m from (1) and (3)
Question. A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.
Ans. Let the natural number be x.
ATQ, x + 12 = 160/x to get x2 + 12x – 160 = 0
(x + 20) (x – 8) = 0
x = 8, x = – 20 (rejected)
Question. If the roots of the quadratic equation (b – c)x2 + (c – a)x + (a – b) = 0 are equal, prove 2b = a + c.
Ans. Find D and let D = 0
(c – a)2 – 4(b – c) (a – b) = 0
Solve to get (a + c – 2b)2 = 0
∴ a + c = 2b
Question. Two water taps together can fill a tank in 6 hours. The tap of larger diameter takes 9 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Ans. Time taken by top of smaller diameter = x hrs
Time taken by larger tap = (x – 9) hrs
ATQ 1/x + 1/(x-9) = 1/6 and get x2 – 21x + 54 = 0
x = 3, x = 18
x = 3 rejeced as x – 9 = – 6 < 0
∴ x = 18 hrs x – 9 = 18 – 9 = 9 hrs
Question. A train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/hr more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
Ans. Equation 54/x + 63/(x+6) = 3, x → speed of train at first, x + 6 → Increased speed.
x = 36, x ≠ – 3.
Question. A farmer wishes to grow a 100 m2 recangular garden. Since he has only 30 m barbed wire, he fences three sides of the rectangular garden letting compound wall of this house act as the fourth side fence. Find the dimensions of his garden.
Ans.
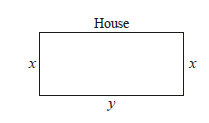
x + y + x = 30, xy = 100
Solve x = 5m, 10 m,
y = 20 m, 10 m
∴ dim. are 5 m × 20 m or 10 m × 10 m
Question. If the price of a book is reduced by ₹ 5, a person can buy 5 more books for ₹ 300. Find the original list price of the book.
Ans. Let original list price = ₹ x
ATQ 300/(x-5) – 300/x = 5
Solve and get x = 20, x = –15 → rejected
∴ ₹ 20 is Answer
Question. The denominator of a fraction is one more than twice the numerator. If the sum of the fraction and its reciprocal is 2(16/21). Find the fraction.
Ans. Fraction is x/(2x+1)
ATQ x/(2x+1) + (2x+1)/x = 2(16/21) = 58/21
Solve to get x = 3, x = -7/11 (rejected)
∴ Answer is Fraction = 3/7.
Question. ₹ 6500 were divided equally among a certain number of persons. If there been 15 more persons, each would have got ₹ 30 less. Find the original number of persons.
Ans. Let original number of persons be x
ATQ 6500/x – 6500/(x+15) = 30
Solve and get x = 50, x = – 65 (rejected).
Question. A train covers a distance of 480 km at a uniform speed. If the speed had been 8 km/hr less, then it would have taken 3 hours more to cover the same distance. Find the original speed of the train.
Ans. Let the speed of the train = x km/hr
ATQ, 480/(x-8) – 480/x = 3
x2 – 8x – 1280 = 0
x = 40, –32 (rejected)
x = 40 km/hr
Question. A fast train takes 3 hours less than a slow train for a journey of 600 km. If the speed of the slow train is 10 km/hr less than the fast train, find the speed of the two trains.
Ans. ATQ 600/x – 600/(x+10) = 3 (Speed of slow train x km/hr)
Solve to get x = 40, x = – 50 (rejected).
∴ Answer is 40 km/hr, 50 km/hr.
Question. A motor boat whose speed is 24 km/hr in still water takes 1 hour more to go 32 km upstream than to return downstream to the same spot. Find the speed of the stream
Ans. Let speed of boat = x
ATQ 32/(24-x) – 32(24+x) = 1
x2 + 64x – 576 = 0
(x + 72) (x – 8) = 0
x = 8 km/hr
x = –72 km/hr (rejected)

